Методы оптимальных решений.

Преподаватель: Солоненко Ольга Александровна

Лекция №1: Оптимальные решения в задачах планирования производства

1. Производственная функция

Производственная функция выражает зависимость результата производства от факторов производства.

Если рассматривать два ресурса: капитал (К) и труд (L), то результатом деятельности экономической системы будем считать объем выпуска (X), то такую производственную функцию можно задать: X = F(K,L).

Объем выпуска удобно исчислять в денежном выражении. Производственная функция называется неоклассической, если она определена при всех неотрицательных значениях аргументов K и L является непрерывной и дважды дифференцируемой по обоим аргументам при всех K≥0 и L≥0 и обладает следующими свойствами:

1. При отсутствии хотя бы одного фактора производство невозможно.

2. При увеличении затрат ресурсов выпуск продукции возрастает >0 >0

3. При увеличении количества одного из используемых ресурсов при постоянном количестве другого ресурса скорость выпуска продукции замедляется <0 <0, где K≥0 L≥0

4. При неограниченном увеличении количества хотя бы одного из используемых ресурсов выпуск продукции неограниченно возрастает.

На практике чаще всего используется следующие производственные функции:

1. Производственная функция Кобба-Дугласа F (K,L) = A - , где А>0 , α€(0,1)

2. Мультипликативная производственная функция F (K,L) = A * , где А, , >0, , ≤1

3. Функция Леонтьева F (K,L) = , где , >0

4. Линейная функция F (K,L) = K+ L, где , >0

5. С постоянной эластичностью замены F (K,L) = A(α* +(1-α) )

В мультипликативной производственной функции параметр А – коэффициент нейтрального технического прогресса (при неизменных ресурсах K,L и неизменных , выпуск тем выше, чем больше А). Параметр € (0,1) и имеет смысл эластичности выпусками по фондам. Коэффициент эластичности выпуска по фондам показывает насколько процентов вырастет выпуск Х при увеличении фондов на 1%.

В производственной функции Кобба-Дугласа параметр А также представляет собой коэффициент нейтрального технического прогресса, коэффициент эластичности выпуска по фондам равен α, а коэффициент эластичности выпуска по труду равен (1-α).

В случае двухфакторной производственной функции средние эффективности ресурсов – это средняя фондоотдача и средняя производительность труда , а предельные эффективности ресурсов – это предельная фондоотдача и предел производительности труда .

В случае мультипликативности производственной функции выпуска зависит от затрат фондов и труда x=F * , средняя фондоотдача = 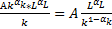, а средняя производительность труда .

2. Модель поведения производителя

Пусть затраты труда и капитала равны K и L, объем выпуска в денежном выражении определяется производственной функцией x=F(k,L), а цены факторов производства (труда и капитала) составляет соответственно , тогда прибыль производителя будет равна П(K,L) = x-

Если считать аксиомой производителя, что он стремится получить наибольшую прибыль, то математическая формулировка задачи производителя следующее: требуется определить такую технологию, то есть такие объемы затрат ресурсов, которые приносят максимальную прибыль.

3. Модель налогообложения.

Ставка акциза (t) определяется, как доля цены товара, взимаемая в виде налога. Если читать все факторы, кроме цены неизменными, то полученную зависимость спроса D=D(p). Точно также можно рассматривать и функцию предложения S=S(p), при этом равновесная цена определяется из условия равенства спроса и предложения S( 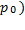= D( )

При введении акциза t (0,1) равновесия спроса и предложения изменятся и новой равновесной ценой станет Р(t). Получится новое условие: .

На потребителя ложится бремя оплаты 2/3 введенного налога, а оставшуюся часть платит производитель.

Увеличение цены приводит к уменьшению объема реализованного спроса и предложения и как следствие к уменьшению выручки производителя.

Максимум прибыли при наличии акциза достигается при меньших затратах и труда и капитала. И как следствие, при меньших объемах производства.

Лекция №2: Система линейных алгебраических уравнений.

Система из К-уравнений первой степени с n неизвестными может быть записана в виде: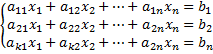

где неизвестные х₁, х₂,х₃ подлежат определению, а коэффициенты а₁₁,а₁₂,а_n, при неизвестной, и свободные члены в₁,в₂…в_к уравнений заданы, притом первый индекс коэффициента совпадает с номером уравнения, в котором содержится данный коэффициент, второй индекс – с номером неизвестной, при которой поставлен коэффициент.

Система линейных алгебраических уравнений называется совместной, если она имеет решение. Совместная система называется определенной или неопределенной, в зависимости от того имеет она одно или более решений. Система называется несовместной или противоречивой, если она не имеет решений.

Две системы линейных алгебраических уравнений с одним и тем же числом неизвестных называются эквивалентными или равносильными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.

Число уравнений в эквивалентных системах может быть различным. В процессе отыскания решений систему уравнений можно подвергать только таким преобразованиям, которые переводят ее в эквивалентную систему.

Относительно любой системы линейных алгебраических уравнений можно задать вопросы:

1. Совместна она или нет?

2. Если она совместна, то каково число решений?

3. Как найти все решения?

Рассмотрим метод Жардана-Гаусса. Метод последовательного исключения неизвестных. Составим матрицу А из коэффициентов при неизвестных системы линейных алгебраических уравнений. Ее принято называть матрицей системы.

Очевидно, систему линейных алгебраических уравнений можно записать в матричной форме: A x=b

Пример: Нужно проверить, является ли вектор , решением системы линейных уравнений, которая задана расширенной матрицей:

Решение: Подставим координаты вектора у вместо неизвестных в данную систему:

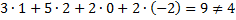
Так как вычисленные значения не совпадают с координатами вектора B. то вектор у не является решением данной системой уравнений.

Элементарные преобразования системы линейных алгебраических уравнений называют преобразования следующих трех типов:

1. Перестановка двух каких-нибудь уравнений системы.

2. Умножение обеих частей одного из уравнений на любое число отличное от 0.

3. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.

Подвергая систему линейных алгебраических уравнений элементарным преобразованиям, можно исключить любую неизвестную из всех уравнений кроме одного. Предположим, что в системе уравнений коэффициент a_rs отличен от нуля, и что мы решили исключить неизвестную X_s из всех уравнений системы кроме одного r – его назвали разрешающим уравнением.

Коэффициент a_rs – это разрешающий коэффициент, x_s – разрешающая неизвестная.

Если умножить разрешающие уравнение системы на какое-нибудь число λ и прибавить к i – уравнению, то все коэффициенты при неизвестных и свободный член i –ого уравнения изменится и примут значение

Неизвестная x_s исключается из i-ого уравнения, если коэффициент при ней станет равным 0. т.е. Для этого необходимо взять λ, как отношение . Исключив, таким образом, неизвестную x_s из всех уравнений системы кроме разрешающего уравнения системы на разрешающего коэффициент и система перейдет в следующую эквивалентную ей новую систему:

Где неизвестная х_s содержится только в разрешающихся уравнениях притом с коэффициентом 1, а остальные коэффициенты при неизвестных и свободные члены связаны с коэффициентами и свободными членами исходной системы формулой :

И они называются формулой исключения.

Если в процессе преобразований появятся уравнения вида х называют нуль уравнениями, которые мы отбрасываем.

Процесс последовательного исключения неизвестных закончится либо тогда, когда мы придем к системе содержащей уравнения вида ноль уравнения, что будет означать несовместность исследуемой системы, либо тогда когда уравнение примет вид: