 |
|
Математическое ожидание и дисперсия дискретной случайной величины. Среднее квадратическое отклонение.
Математические операции над случайными величинами
Прерывные случайные величины X и Y называются независимыми, если не зависимы при любых i и j, события X=xi и Y=yj.
Пусть случайная величина X принимает x1, x2, x3, …, xn с вероятностями p1, p2, p3 ,…, pn, соответственно, а Y-значения y1, y2, y3, …, ym, с вероятностями q1, q2, q3, …, qm.
а) Суммой случайных величин X и Y называется новая случайная величина Z=X+Y, которая принимает все значения вида zij=xi+yj(i=1,2,..n; j=1,2,...,m) с вероятностями pij, причем pij=P(X=xi; Y=yj)=P(X=xi)*PX=xi(Y=yj).
Если случайные величины X и Y независимые, то pij= pi+ qj.
Аналогично определяется разность и произведение случайных величин.
б) Разностью ( произведением) случайных величин X и Y называется новая случайная величина Z=X-Y (Z=XY), которая принимает все значения вида zij=xi-yj (zij=xiyj) с такими же вероятностями, с какими случайная величина Z=X+Y принимает соответствующие значения, т.е. pij= pi+ qj.
в) Произведением kX случайной величины Х на постоянную величину k называется новая случайная величина Z=kX, которая с теми же вероятностями, что и Х, принимает значения, равные произведениям значений случайной величины Х на k, т.е. =xi2.
г) Квадратом случайной величины Х, т.е. Х2, называется новая случайная величина Z=X2, которая с теми же вероятностями, что и Х, принимает значения, равные квадратам значений случайной величины Х, т.е. zi=xi2.
Числовые характеристики дискретных случайных величин
а) Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности, т.е.:

или, если случайная величина может принимать счетное число значений,  причем лишь в случае абсолютной сходимости ряда.
причем лишь в случае абсолютной сходимости ряда.
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
1. Для первичного ряда:
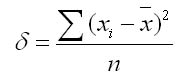
2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
Примеры нахождения cреднего квадратического отклонения: Пример 1, Пример 2
Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:

где р — доля единиц в совокупности, обладающих определенным признаком;
q — доля единиц, не обладающих этим признаком.