Главная | Обратная связь

Повторные испытания

1.формула Бернулли. Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.

Предположим, что несколько одинаковых машин в одних и тех же условиях перевозят груз. Любая машина может выйти из строя при этих перевозках. Пусть вероятность выхода из строя одной машины не зависит от выхода из строя других машин. Это значит, что рассматриваются независимые события (испытания). Вероятности выхода из строя каждой из этих машин примем одинаковыми. .

Пусть, в общем случае, производится независимых испытаний. Ставится задача определения вероятности того, что ровно в 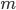испытаниях наступит событие если вероятность наступления этого события в каждом испытании равна В случае с машинами это могут быть вероятности выхода из строя ровно одной машины, ровно двух машин и т.д.

Определим вначале вероятность того, что в первых 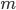испытаниях событие наступит, а в остальных испытаниях — не наступит. Вероятность такого события может быть получена на основании формулы вероятности произведения независимых событий где

Так как рассматривалась только одна из возможных комбинаций, когда событие произошло только в первых 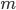испытаниях, то для определения искомой вероятности нужно перебрать все возможные комбинации. Их число будет равно числу сочетаний из элементов по 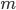т.е.

Таким образом, вероятность того, что событие наступит ровно в 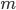испытаниях определяется по формуле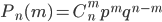

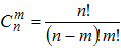
Пример. В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке известна и равна 0,5. Какова вероятность выигрыша ровно трех предметов?

Решение. По формуле Бернулли находим

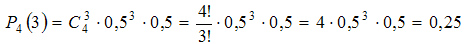
2 Формула Пуассона.

Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний . При больших значениях пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.

Теорема. Если вероятность наступления события в каждом испытании постоянна и мала, а число независимых испытаний достаточно велико, то вероятность наступления события ровно 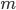аз приближенно равна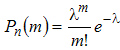

Доказательство. Пусть даны вероятность наступления события в одном испытании и число независимых испытаний . Обозначим . Откуда . Подставим это выражение в формулу Бернулли:

При достаточно большом н и небольшом м все скобки, за исключением предпоследней, можно принять равными единице, т.е.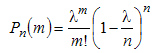

Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при 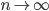т.е. найти предел 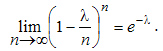Тогда получим

Пример. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.

Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).

Находим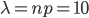

воспользуемся формулой Пуассона

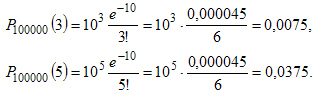
3. Локальная и интегральная теоремы муавра-лапласса.

 

ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА — ЛАПЛАСА

Ранее решена задача о нахождении вероятности того, что в n независимых испытаниях событие состоится m раз. Но часто нужно знать вероятность наступления события не одно определенное число раз, а число раз, заключенное в некоторых границах.

Например, пусть требуется найти вероятность того, что из 1000 новорожденных мальчиков будет от 455 до 545 включительно. Искомое событие состоит в том, что мальчиков будет или 455, или 456 и т. д. до 545. По теореме сложения вероятность искомого события равна сумме вероятностей указанных распределений детей по полу: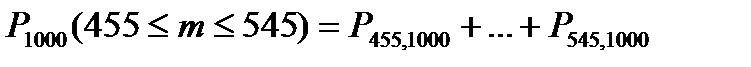

Каждое слагаемое нетрудно найти по локальной формуле Муавра — Лапласа при известной вероятности рождения мальчика, и задача, кажется, будет решена. Но вычисление 91 слагаемого и последующее сложение их очень утомительно, а поэтому предложенный метод решения неприемлем.

Поэтому возникает необходимость найти иной метод определения вероятностей таких событий, который обеспечивал бы получение до-статочно точных значений искомых вероятностей посредством простых выкладок. Ответ на поставленную задачу дает интегральная теорема Муавра – Лапласа.

Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях событие А состоится число раз, заключенное в границах от а до b включительно (а < b), приближенно равна:

где функция Ф (х) определяется равенством

Формула называется интегральной формулой Муавра— Лапласа. Получаемые по интегральной и локальной формулам Муавра — Лапласа вероятности достаточно точны, если произведение nр составляет несколько сотен. В задачах, не требующих большой точности ответа, можно пользоваться этими формулами и в случаях, когда произведение np имеет небольшое значение, однако не меньшее 20.

Функция Ф(х), которая определена равенством, указанным выше, табулирована. Чтобы успешно пользоваться этой таблицей, необходимо знать свойства функции Ф(х). Рассмотрим их.

1. Функция Ф(х) нечетная, т. е. Ф (—х) = — Ф(х).

2. Функция Ф(х) монотонно возрастающая.

3. Предел функции Ф(х) при равен единице.

4. Для всех значений х > 5 можно считать, что . Уже Ф (5) = 0,99999994, а тем более Ф (х) » 1, если х > 5, так как при увеличении х функция Ф (х) возрастает, но не может превосходить. Поэтому в таблицах функция дана для значений х > 5.

Пример. Найти вероятность того, что из 1000 новорожденных будет от 456 до 545 мальчиков, если вероятность рождения мальчика равна 0,515.

Решение. x2 =1.898, x1 =-3.797. P=0.5(Ф(1,898)+Ф(3,797))=0,9711.