 |
|
Уравнение линии регрессии.
Регрессия.
 – св, определенные на 1 вероятностном пространстве, К- класс функций. Будем называть св
– св, определенные на 1 вероятностном пространстве, К- класс функций. Будем называть св  представленную в виде
представленную в виде  регрессией Y на X если выполнено
регрессией Y на X если выполнено 
Уравнение линии регрессии.


 тогда уравнение линии регрессии Y на X:
тогда уравнение линии регрессии Y на X:  ; X на Y:
; X на Y: 
Элементы мат статистики.
По данным наблюдений определяются вероятности определенных случайных событий, делаются вывод о характеристиках наблюдаемых величин, проверяются гипотезы о распределениях наблюдаемой величины и о характеристике зависимости между разными случайными величинами.
1)  X –нсв, тогда выборкой объема n из Х назовем
X –нсв, тогда выборкой объема n из Х назовем  , где
, где  – независимая случайная величина, имеющая то же распределение, что и Х.
– независимая случайная величина, имеющая то же распределение, что и Х.
2) Th об эмпирической функции распределения
 – выборка из св Х.
– выборка из св Х.  эмпирическая функция распределения построенная по данной выборке, тогда для
эмпирическая функция распределения построенная по данной выборке, тогда для 
Доказательство: Возьмем в качестве А взять событие {X<x}, то Р – вероятность события А.  Если произведено n независимых испытаний, то относительная частота наступления
Если произведено n независимых испытаний, то относительная частота наступления  где m- число Xi для которых Xi<x
где m- число Xi для которых Xi<x
тогда 
3)  – выборка из св Х , ϴ - некий параметр распределения Х, тогда оценкой ϴ будем называть св
– выборка из св Х , ϴ - некий параметр распределения Х, тогда оценкой ϴ будем называть св 

4)  – выборка , ϴ - некий параметр распределения
– выборка , ϴ - некий параметр распределения 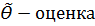 , будем называть оценку
, будем называть оценку  не смещенной, если
не смещенной, если 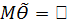
5)  – выборка , ϴ - некий параметр распределения
– выборка , ϴ - некий параметр распределения 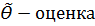 , будем называть оценку
, будем называть оценку  самостоятельной, если
самостоятельной, если 
6)  – выборка , ϴ - некий параметр распределения,
– выборка , ϴ - некий параметр распределения,  не смещенная, тогда ее можно назвать эффективной, если она имеет наименьшую Dϴ среди других.
не смещенная, тогда ее можно назвать эффективной, если она имеет наименьшую Dϴ среди других.
7)  – выборка из св Х, тогда выборочным средним назовем
– выборка из св Х, тогда выборочным средним назовем 
8)Th о выборочном среднем
Х – случайная величина имеющая МХ=а тогда  будет не смещенная, самостоятельная и эффективная оценка параметра а.
будет не смещенная, самостоятельная и эффективная оценка параметра а.
Доказательство:
Не смещенность 
Самостоятельность  ,
,  независимы, поэтому по закону больших чисел, если Х имеет DX или по Th Хинчина, если ее нет, мы получим
независимы, поэтому по закону больших чисел, если Х имеет DX или по Th Хинчина, если ее нет, мы получим 
т.е. 
9)  – выборка из св Х, тогда выборочной дисперсией данной выборки назовем
– выборка из св Х, тогда выборочной дисперсией данной выборки назовем 
10) Th о выборочной дисперсии X – св, имеющая DX=  тогда S2 будет самостоятельной и смещенной оценкой.
тогда S2 будет самостоятельной и смещенной оценкой.
11)  – выборка из св Х, тогда исправленной выборочной дисперсией данной выборки назовем
– выборка из св Х, тогда исправленной выборочной дисперсией данной выборки назовем 
12) Th о исправленной выборочной дисперсии X – св,  будет самостоятельной и несмещенной оценкой.
будет самостоятельной и несмещенной оценкой.
13)  – выборка из св Х, а=MX, тогда уточненной выборочной дисперсией назовем
– выборка из св Х, а=MX, тогда уточненной выборочной дисперсией назовем 
14) Соответствие между эмпирическими и теоретическими св.
| Теоретические характеристики | Эмпирические характеристики |
Функция распределения 
| Э.Ф.Р. 
|
Плотность распределения 
| Гистограмма |
| Математическое ожидание MX | Выборочное среднее 
|
| Дисперсия DX | 1) Выборочная S2
2) Исправленная  3) Уточненная
3) Уточненная 
|
Специальные распределения статистики
1)  , имеющие стандартное нормальное распределение, тогда св
, имеющие стандартное нормальное распределение, тогда св
 –распределение по закону кхи квадрат с n степенями свободы. Плотность распределения имеет вид
–распределение по закону кхи квадрат с n степенями свободы. Плотность распределения имеет вид

2)  , с независимым стандартным нормальное распределение, тогда св
, с независимым стандартным нормальное распределение, тогда св
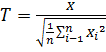 распределена по закону Стьюдента с n степенями свободы
распределена по закону Стьюдента с n степенями свободы

при n ∞это распределение близко к стандартному нормальному распределению.
Интервальные оценки
1)  - параметр распределения Х 0<P<1, тогда доверительным интервалом для параметра ϴ с доверительной вероятностью Р построенной по выборке
- параметр распределения Х 0<P<1, тогда доверительным интервалом для параметра ϴ с доверительной вероятностью Р построенной по выборке  из Х
из Х
Называется интервал с границами α  и
и  такой что
такой что
p{ α  p назовем доверительной вероятностью.
p назовем доверительной вероятностью.
*не всегда удается достичь точного равенства, поэтому как правило
p{ α 
2)  - параметр распределения св Х, а
- параметр распределения св Х, а  –выборка из Х. Тогда достаточной статистикой для параметра ϴ построенной по выборке
–выборка из Х. Тогда достаточной статистикой для параметра ϴ построенной по выборке  св
св  распределение, которое известно и не зависит от ϴ.
распределение, которое известно и не зависит от ϴ.
3) 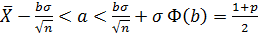
Построение доверительного интервала для а при известном 
 –выборка, Х распределена нормально с параметрами а и
–выборка, Х распределена нормально с параметрами а и  . Тогда достаточной статистикой для «а» назовем
. Тогда достаточной статистикой для «а» назовем  где
где  – исправленная выборочная дисперсия
– исправленная выборочная дисперсия
Y будет иметь распределение Стьюдента с n-1 степенью свободы. Ру(х) является четной => можно выбрать симметричный интервал ,так что р={-b<Y<b} число b определяется по таблице в Гмурмане. Доверительный интервал будет иметь вид

Построение доверительного интервала для  при известном а
при известном а
 –выборка
–выборка  –уточненная выборочная дисперсия тогда достаточной статистикой будем считать
–уточненная выборочная дисперсия тогда достаточной статистикой будем считать  которая имеет хи квадрат распределение. Числа а и b, для которых выполнено р={a<Y<b} можно подобрать так, что это будет эквивалентно
которая имеет хи квадрат распределение. Числа а и b, для которых выполнено р={a<Y<b} можно подобрать так, что это будет эквивалентно  q по Гмурмону взяв в расчет P и число степеней свободы.
q по Гмурмону взяв в расчет P и число степеней свободы.
Построение доверительного интервала для  при неизвестном а
при неизвестном а
 тогда оценка будет иметь вид
тогда оценка будет иметь вид 
Проверка статистических гипотез
1) Статистическая гипотеза – любое предположение о виде распределения Х или о ее параметрах. Она будет простой, если при ее выполнение, распределение Х становится однозначным.
2) Ошибка 1 рада: непринятие правильной гипотезы.
3) Ошибка 2 рода: принятие не верной гипотезы.
4) Проверка гипотеза:
| Гипотеза | Принимается | Не принимается |
| Истина | Правильное решение | Ошибка 1 рода |
| Ложь | Ошибка 2 рода | Правильное решение |
5) Для того что бы принять или отвергнуть выдвинутую гипотезу, по выборке 
Составляется св  , которая при истинности гипотезы имеет какое-то известное распределение. Задается 0<α<1 называемый уровнем значимости, как правило выбирают α близким к 0. По известному закону распределения для ϴ находится критическая область
, которая при истинности гипотезы имеет какое-то известное распределение. Задается 0<α<1 называемый уровнем значимости, как правило выбирают α близким к 0. По известному закону распределения для ϴ находится критическая область  такая что
такая что 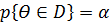
Если выбранное значение ϴ оказывается в критической области, то гипотеза отвергается, а если не попадает, то считается, что гипотеза не противоречит данным.
6) Правило, по которому принимается или отвергается называется Критерием.
7) Вероятность ошибки 1 рода назовем Уровнем значимости для данного критерия, а вероятность совершить ошибку 2 рода называется мощностью.
Проверка гипотезы о виде распределения:
1) Критерий  (Пирсона)
(Пирсона)
Имеется вариационный ряд (дискретный\интервальный) и проверяется гипотеза о том, что Х имеет функцию распределения  . Для применения критерия Пирсона исходный вариационный ряд записывают в интервальной форме. Для каждого интервала
. Для применения критерия Пирсона исходный вариационный ряд записывают в интервальной форме. Для каждого интервала
[αi,βi] вычисляются теоретические вероятности попадания Х в интервал по формуле

После вычисления  производят вычисление теоретических частот попадания
производят вычисление теоретических частот попадания 
n – общее число наблюдений после составляется св 
 –эмпирическая частота. Если гипотеза верна, то данная св имеет χ2 распределение с
–эмпирическая частота. Если гипотеза верна, то данная св имеет χ2 распределение с
m-k-1 степенями свободы. Где m – число интервалов, k – число параметров распределения определенной по выборке. По числу степеней свободы и заданному уровню значимости α определяется число 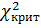 .
. 

Условия применения: 1) В каждом интервале должно быть не менее 5 значений (если меньше, то соединяются соседние) 2) Общее число набл не <30. 3)Интервал должны быть от -∞ до + ∞
(см на стр. 2)
Критерий Колмогорова
Для применения кк по результатам наблюдения составляют  , после находится св
, после находится св

Th Колмогорова
Для любой св Х и  >0 будет выполняться
>0 будет выполняться 

Если  гипотеза отвергается. Иначе не противоречит данным.
гипотеза отвергается. Иначе не противоречит данным.
