 |
|
ДВУМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Двумерной называют случайную величину (Х, Y), возможные значения которой есть пары чисел (х, у). Составляющие Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Двумерную величину геометрически можно истолковать как случайную точку М(Х, Y) на плоскости хОу, либо как случайный вектор 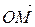 .
.
Функция распределения двумерной случайной величины (Х, Y) определяется соотношением F(x; y) = P(X < x, Y < y) и геометрически определяет вероятность попадания случайной точки (Х, Y) в бесконечный квадрат с вершиной в точке (Х, Y), лежащий левее и ниже ее.
Дискретной называют двумерную величину, составляющие которой дискретны; непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной двумерной случайной величины может быть задан с помощью таблицы:
| X Y | х1 | х2 | … | хi | … |
| у1 | p11 | p21 | … | pi1 | … |
| у2 | p12 | p22 | … | pi2 | … |
| … | … | … | … | … | … |
| yj | p1j | p2j | … | pij | … |
| … | … | … | … | … | … |
где x1<x2<…<xi<…; y1<y2<…<yj<…;
pij – вероятность события, заключающаяся в одновременном выполнении равенств Х = хi; Y = yj, при этом 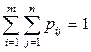 .
.
Функция распределения двумерной дискретной случайной величины определяется равенством  .
.
Закон распределения непрерывной двумерной случайной величины может быть задан с помощью функции плотности вероятности f(x,y), удовлетворяющей условиям:
1) f(x; y) ³ 0; 2)  .
.
Если все возможные значения (Х, У) принадлежат конечной области D, то  .
.
Вероятность попадания случайной точки (Х, У) в область D определяется равенством  .
.
Связь плотности вероятности f(x, y) и функции распределения F(x ,y) двумерной непрерывной случайной величины задается соотношениями 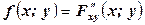 ;
;  .
.
Законы распределения составляющих непрерывной двумерной случайной величины вычисляются по формулам 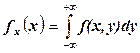 ;
;  .
.
Для нахождения законов распределения составляющих двумерной дискретной случайной величины надо суммировать вероятности в таблице по строкам или по столбцам.
Условным распределением составляющей Х при Y = уj (j – сохраняет одно и то же значение при всех возможных значения Х) называют совокупность условных вероятностей  ,
,  , …,
, …,  .
.
Аналогично определяется условное распределение Y. Условные вероятности составляющих X и Y вычисляются соответственно по формулам
 ;
;  .
.
Для непрерывных случайных величин формулы вычисления условных плотностей распределения выглядят так:
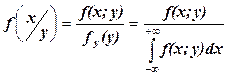 ;
;  .
.
Числовые характеристики составляющих вычисляются по формулам:
 ;
;  – для дискретных случайных величин;
– для дискретных случайных величин;
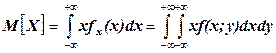 ;
;  – для непрерывных случайных величин;
– для непрерывных случайных величин;
 ;
;  ;
;
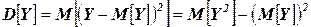 ;
;  .
.
Точка  называется центром рассеяния двумерной случайной величины (X, Y).
называется центром рассеяния двумерной случайной величины (X, Y).
Для оценки тесноты взаимосвязи составляющих вычисляют корреляционный момент или ковариацию 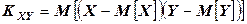 .
.
Корреляционный момент удобно вычислять по формуле 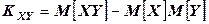 , где
, где 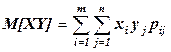 в дискретном и
в дискретном и 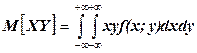 в непрерывном случае.
в непрерывном случае.
Степень связи между составляющими в чистом виде характеризует так называемый нормированный корреляционный момент или коэффициент корреляции 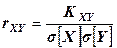 , обладающий следующими свойствами: 1)
, обладающий следующими свойствами: 1)  2)
2)  тогда и только тогда, когда случайные величины связаны линейной зависимостью.
тогда и только тогда, когда случайные величины связаны линейной зависимостью.
Случайные величины Х, У называются некоррелированными, если КXY = 0, а следовательно, и 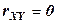 .
.
Случайные величины Х, Y называются независимыми, если вероятность одной из них принять значение, лежащее в любом промежутке области ее значений, не зависит от того, какое значение приняла другая величина.
Для двумерной дискретной случайной величины, представленной в виде таблицы распределения, условие независимости составляющих Х и Y состоит в том, что для любых i и j  , где
, где 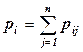 ,
,  . Внешне это выражается в том, что строки и столбцы таблицы пропорциональны.
. Внешне это выражается в том, что строки и столбцы таблицы пропорциональны.
Для двумерной непрерывной случайной величины условие независимости состоит в том, что 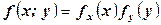 .
.
Независимые случайные величины всегда некоррелированны. Обратное, вообще говоря, неверно (т.е. некоррелированные величины могут быть зависимыми).
Условным законом распределения случайной величины Yx называется закон распределения случайной величины Y при условии, что Х = х.
Функциональная зависимость М[Yx] = j(x) называется регрессией случайной величины Y на случайную величину Х.
Среднее значение квадрата отклонения 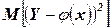 достигает минимально возможного, когда j(х) – регрессия Y на Х (минимизирующее свойство регрессии).
достигает минимально возможного, когда j(х) – регрессия Y на Х (минимизирующее свойство регрессии).
Функция  из класса функций
из класса функций 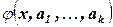 определяемых набором параметров а1 , …, аk называется среднеквадратичной регрессией Y на Х в этом классе функций, если среднее значение квадрата отклонения
определяемых набором параметров а1 , …, аk называется среднеквадратичной регрессией Y на Х в этом классе функций, если среднее значение квадрата отклонения  достигает на наборе параметров
достигает на наборе параметров  минимального значения для всех функций этого класса.
минимального значения для всех функций этого класса.
Простейшей функцией является линейная: 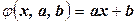 . Уравнение прямой среднеквадратичной регрессии Y на Х выглядит так:
. Уравнение прямой среднеквадратичной регрессии Y на Х выглядит так: 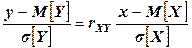 .
.
Аналогично уравнение прямой среднеквадратичной регрессии Х на Y:  .
.
16.1. Восстановить законы распределения составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Найти условное распределение случайной величины Х при условии, что Y= y1. Найти условное распределение случайной величины Y при условии, что Х = х2.
| Х Y | |||
| 0,2 | 0,18 | 0,22 | 0,16 |
| 0,8 | 0,08 | 0,16 | 0,2 |
16.2. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины.
| Х Y | 0,8 | 1,5 | |
| 0,2 | 0,2 | 0,1 | |
| 0,2 | 0,1 | 0,2 |
16.3. По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна 0,7. Составить таблицу распределения двумерной случайной величины (Х; Y), где Х – число попаданий, Y – число промахов. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Определить, зависимы или нет составляющие Х и Y.
16.4. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной непрерывной случайной величины (Х; Y), имеющей плотность  , где D – треугольник ограничен-ный линиями: х = 0; у = 0; х + у = 1. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения
, где D – треугольник ограничен-ный линиями: х = 0; у = 0; х + у = 1. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения  .
.
16.5. Двумерная непрерывная случайная величина (Х; Y) подчинена закону распределения с плотностью 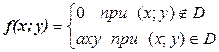 , где D – квадрат
, где D – квадрат 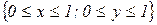 . Найти коэффициент а. Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
. Найти коэффициент а. Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
16.6. Двумерная непрерывная случайная величина (Х; Y) распределена равномерно в круге радиуса R= 5 с центром в начале координат. Доказать, что составляющие Х и Y являются зависимыми и некоррелированными величинами.
16.7. Найти плотность вероятности f(x; y) двумерной случайной величины (Х; Y), имеющей функцию распределения  .
.
16.8. Найти уравнения прямых линий средних квадратических регрессий Y на Х и Х на Y двумерной случайной величины (Х; Y), заданной таблицей распределения:
| Х Y | 0,2 | 0,5 | |||||
| 0,3 | 0,1 | ||||||
| 1,5 | 0,2 | 0,1 | |||||
| 0,1 | 0,2 | ||||||
16.9. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины.
| Х Y | 0,5 | ||
| 0,5 | 0,2 | 0,1 | 0,2 |
| 0,1 | 0,3 | 0,1 |
16.10. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной непрерывной случайной величины (Х; Y), имеющей плотность 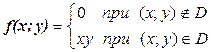 , где D – прямоугольник
, где D – прямоугольник 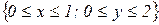 . Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения
. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения  .
.
16.11. Двумерная непрерывная случайная величина (Х; Y) подчинена закону распределения с плотностью 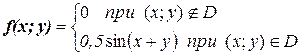 , где D – квадрат
, где D – квадрат  . Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
. Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
16.12.Найти плотность вероятности f(x; y) двумерной случайной величины (Х; Y), имеющей функцию распределения 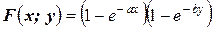 .
.
16.13. Найти уравнения прямых линий средних квадратических регрессий Y на Х и Х на Y двумерной случайной величины (Х; Y), заданной таблицей распределения:
| Х Y | 1,5 | ||
| 0,3 | 0,1 | 0,1 | |
| 0,1 | 0,2 | ||
| 0,1 | 0,1 |