Главная | Обратная связь

Распределение переменных величин.

Нормальное распределение (называемое также распреде­лением Гаусса) характеризуется тем, что крайние значения при­знака в нем встречаются достаточно редко, а значения, близкие к средней величине, — часто. Нормальное распределение возникает, когда данная случайная величина представляет собой сумму боль­шого числа независимых случайных величин, каждая из которых играет в образовании всей суммы незначительную роль.

Нормальное распределение имеет колоколообразную форму, значения его моды, медианы и среднего арифметического равны. Это распределение описывается формулой:

где g - высота кривой прямо над всяким заданным значением X на графике распределения частот;

m - среднее распределения частот большой выборки;

s - стандартное отклонение этого распределения.

m и s — числа, которые определяют положение кривой относительно числовой оси и регулирует ее размах.

 

 

Рис. 1. Кривая нормального распределения

 

Из рисунка видно, что 95% значений признака вариационного ряда не отклоняются от средней (m) влево и вправо больше, чем на 1,96s. Как только они становятся больше 1,96s, они как бы перешагивают порог (границы) 95%. Тогда говорят, что различия соответствуют 5% уровню (вероятность Р - 0,05) и находятся на уровне первого порога. Но различия могут быть и большими, хотя 99% значений отклоняются от средней не больше, чем на + 2,58s. Если отклонения больше указанных границ, то говорят о превышении второго порога; различия достигли 1% уровня (Р - 0,01). Если 99,9% значений отклоняются от средней не больше, чем на + 2,58s, то говорят, что они соответствуют третьему порогу или уровню 0,1% (вероятность Р - 0,001).

Вероятность выражается числами от 0 до 1: значение, равное 0, указывает, что событие навернека не произойдет (или что гипотеза неверна); значение, равное единице, указывает, что событие, вероятно, произойдет (или что гипотеза в одинаковой мере может считаться верной или неверной). В практике величина вероятности часто выражается в процентах.

Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения.

Все многообразие нормальных распределений м.б. сведено к одной кривой, если применить Z–преобразование ко всем возможным изменением свойств. Тогда каждое свойство будет иметь М_z=0 и D_z(σ_z)=1 – это единичное нормальное распределение.

Свойства единичного нормального распределения:

1. Единицы измерения единичного нормального распределения является σ.

2. Кривая приближается к оси Z асимптомотически.

3. Кривая симметрична относительно Мо. А_s, Е_х = 0.

4. Кривая имеет характерный изгиб. Точка перегиба лежит ровно на расстоянии 1σ от М.

5. Площадь между кривой и осью Z = 1.

Отсюда вытекает правило 3σ:

1. В пределах М±1σ располагается 0,6826, или 68,26% площади всех измерений, количества наблюдений;

2. В пределах М±2σ - 0, 9544, или 95,44%;

3. В пределах М±3σ - 0,9972, или 99,72%, количества наблюдений.

Распределение отклоняющееся от нормального. Анализ эмпирических распределений. Основная задача анализа вариационных рядов — выявление подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов — достигается увеличением объема исследуемой совокупности при одновременном уменьшении интервала ряда.

Статистики описывают четыре свойства или особенности выборок: центральную тенденцию, изменчивость симметрию и эксцесс.

Симметричное распределение — распределение, форма графика которого по одну сторону от моды является зеркальным отображением формы графика этого распределения по другую сторону от моды. Практически точно симметричные полигоны частот и гистограммы почти никогда не встречаются. Один из наиболее важных свойств распределения частот — степень асимметрии. Степень асимметрии распределения частот для выборки называется просто его асимметрией.

Асимметрия – стерпень отклонения графика, распределения частот от симметричного вида относительно среднего значения.

Асимметрическое распределение — распределение, которое не является симметричным и может иметь с одной стороны более длинный "хвост", чем с другой. Два крайних участка распределения, на которых значения частот невелики, принято называть "хвостами" распределения.

Рис.2. Левосторонняя (положительная) асимметрия Аs >0

Рис.3. Правосторонняя (отрицательная) асимметрия Аs<0

Показатель асимметрии (А_s) вычисляется по формуле:

Иногда важно получить представление о том, являются ли полигон частот или гистограмма островершинными (рис. 4) или плоскими (рис. 5). Эксцесс – греческое слово, обозначающее свойство “остроконечности“ кривой.

Эксцесс – это мера плосковершинности или остроконечности графика распределения измеренного признака.

Показатель эксцесса (E_x) определяется по формуле:

.

Рис.4.Островершинное распределение Ex>0

Рис.5. Плосковершинное распределение Ex<0

В тех случаях, когда в распределении наблюдаются чаще средние значения, образуется распределение с положительным эксцессом. Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом.

Показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако они часто дают определенные указания для дальнейшего исследования. Например, появление значительного отрицательного эксцесса может указывать на качественную неоднородность совокупности.

При проведении анализа вариационных рядов целесообразно свести эмпирическое распределение к одному из хорошо исследованных видов теоретического распределения, рассматриваемых математической статистикой. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационных рядов сводится к сопоставлению эмпирического и теоретического распределений и определению степени различия между ними.

В статистике широко используются различные виды теоретических распределений — нормальное распределение, биноминальное распределение, распределение Пуассона и др. Каждое из теоретических распределений имеет свою область применения в различных отраслях знания.

Более полная и точная проверка соответствия распределения гипотезе о нормальном законе распределения производится с использованием специальных критериев -критерий К.Пирсона, критерий Колмагорова.

Критерий Пирсона. Часто утверждают, что данные нормальны или приближенно нормальны, подразумевая под этим, что некоторое множество значений распределено достаточно близко к нормальному. Для проверки такой гипотезы можно применять критерий c² . Любое множество значений, относительно которых предполагается, что они распределены нормально, можно сравнить с нормальным распределением с той же средней, стандартным отклонением и суммарной частотой, что и наблюденные данные. Таким образом, критерий c² становится критерием нормальности данных, средством проверки гипотезы о нормальности определенного распределения.

В общем случае критерий c² может применяться везде, где множество наблюденных значений сравнивается с соответствующим множеством теоретических значений и данные рассматриваются как результаты случайной выборки.

Критерий хи-квадрат (c²) Пирсона -мощный непараметрический критерий сравнения частот двух эмпирических распределений или эмпирического и теоретического.

Критерий хи-квадрат используется для сравнения двух частот, двух эмпирических или эмпирического и критического.

Применение критерия требует, чтобы объем распределений был не менее 30 вариант, а частота не менее 5.

Формула критериятакова:

где f_i - каждая частота двух сопоставляемых выборок, соответствующая единому аргументу;

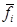- среднее значение данной частоты по двум выборкам (или ожидаемая частота).

После того как статистика c² вычислена, ее величина сравнивается с распределением c² , которое соответствует данному числу степеней свободы. Эта процедура известна как проверка значимости критерия c² .

С помощью величины c² по специальным таблицам определяется вероятность P(c²). Входами в таблицу являются значения c² и число степеней свободы k = n - 1. На основе P выносится суждение о существовании или несуществовании расхождения между эмпирическим и теоретическим распределениями.

Величина c² не говорит о силе связи между переменными, а лишь указывает на вероятность существования такой связи. Для определения интенсивности связи необходимо использовать соответствующие меры связи.

Критерий Колмагорова 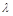предназначен для сопоставления 2-х распределений:

1. Эмпирического с теоретическим, равномерным или нормальным.

2. Одного эмпирического распределения с другим эмпирическим распределением.

Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является максимальной и оценить достоверность этого расхождения.

Ограничения критерия :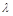

1. Критерий требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо, чтобы .

2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение.

Алгоритм расчета абсолютной величины разности d между эмпирическим и равномерным распределениями

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (1 столбец).

2. Подсчитать относительные эмпирические частоты (частости) для каждого разряда по формуле:

,

где — эмпирическая частота по данному разряду;

n — общее количество наблюдений.

Занести результаты во 2-й столбец.

3. Подсчитать накопленные эмпирические частости по формуле:

,

где — частость, накопленная на предыдущих разрядах; — порядковый номер разряда; — эмпирическая частость данного -го разряда.

Занести результаты в третий столбец таблицы.

4. Подсчитать накопленные теоретические частости для каждого разряда по формуле:

,

где — теоретическая частость, накопленная на предыдущих разрядах; — порядковый номер разряда; 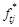— теоретическая частость данного разряда.

Занести результаты в 4-й столбец таблицы.

5. Вычислить разности между эмпирическими и теоретическими накопленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов)

6. Записать в пятый столбец абсолютные величины полученных разностей без их знака. Обозначить их как .

7. Определить по пятому столбцу наибольшую абсолютную величину разности .

8. По ст.таблице определить и рассчитать критические значения для данного количества наблюдений .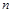

Если равно критическому значению или превышает его, различия между распределениями достоверны.