 |
|
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Числовая последовательность — это последовательность элементов числового пространства.
Операции над последовательностями
На множестве всех последовательностей элементов множества  можно определить арифметические и другие операции, если таковые определены на множестве
можно определить арифметические и другие операции, если таковые определены на множестве  . Такие операции обычно определяют естественным образом, т. е. поэлементно.
. Такие операции обычно определяют естественным образом, т. е. поэлементно.
Пусть на множестве  определена определена  -арная операция -арная операция  : :
 Тогда для элементов
Тогда для элементов  , ,  , …, , …,  множества всех последовательностей элементов множества множества всех последовательностей элементов множества  операция операция  будет определяться следующим образом: будет определяться следующим образом:

|
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей 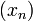 и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что 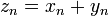 .
.
Разностью числовых последовательностей 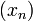 и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что  .
.
Произведением числовых последовательностей  и
и 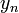 называется числовая последовательность
называется числовая последовательность  такая, что
такая, что  .
.
Частным числовой последовательности  и числовой последовательности
и числовой последовательности 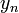 , все элементы которой отличны от нуля, называется числовая последовательность
, все элементы которой отличны от нуля, называется числовая последовательность  . Если в последовательности
. Если в последовательности 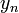 на позиции
на позиции  всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность
всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность  .
.
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
Предел последовательности
Основная статья: Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Теоремы о пределах
- Бесконечно большие и бесконечно малые.
Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < dимеет место неравенство |f(x)| > M.
limx® a=Ґ
- Функция ограниченная при x® a.
- Функция ограниченная при x® Ґ.
- Теорема. Если limx® a f(x)=b, то функция f(x) ограниченная при x® a.
- Бесконечно малые и их свойства. limx® a a(x)=0
Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® af(x)=b, то можно записать f(x)=b+a(x).
Теорема. 2. Если limx® a a(x)=0 и a(x) № 0, то 1/a® Ґ.
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
- Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) Ј z(x) Ј v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах").
Первый замечательный предел

 (второй замечательный предел).
(второй замечательный предел).
ФУНКЦИЯ
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной  однозначно определяет значение выражения
однозначно определяет значение выражения  , а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
, а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
Способы задания функции
[править]Аналитический способ
Функция, как математический объект, представляет собой бинарное отношение, удовлетворяющее определенным условиям. Функцию можно задать непосредственно как множество упорядоченных пар, например:  есть функция
есть функция  . Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
. Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
Для задания функции пользуются выражением: 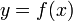 . При этом,
. При этом,  есть переменная, пробегающая область определения функции, а
есть переменная, пробегающая область определения функции, а  — область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
— область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
Пусть имеется множество  яблоко, самолет, груша, стул
яблоко, самолет, груша, стул  и множество
и множество  человек, паровоз, квадрат
человек, паровоз, квадрат  . Зададим функцию f следующим образом:
. Зададим функцию f следующим образом:  (яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)
(яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)  . Если ввести переменную x, пробегающую множество
. Если ввести переменную x, пробегающую множество  и переменную y, пробегающую множество
и переменную y, пробегающую множество  , указанную функцию можно задать аналитически, как:
, указанную функцию можно задать аналитически, как: 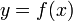 .
.
Аналогично можно задавать числовые функции. Например:  , где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение
, где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение  не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее. Это синтаксическое соглашение является крайне удобным и оправданным.
[править]Графический способ
Числовые функции можно также задавать с помощью графика. Пусть  — вещественная функция n переменных.
— вещественная функция n переменных.
Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис (  ). Каждой точке функции сопоставим вектор:
). Каждой точке функции сопоставим вектор:  . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим «школьное» определение графика функции.
Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.
Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике).
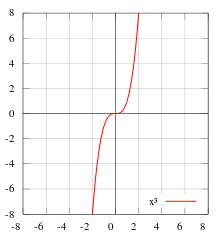
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областяхматематического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.


 — пример нечётной функции.
— пример нечётной функции.


 — пример чётной функции.
— пример чётной функции.

 нечётная
нечётная


 ни чётная, ни нечётная.
ни чётная, ни нечётная.
Другие определения:
- Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
- Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричнаяотносительно оси ординат).
- Индифферентная функция[источник не указан 54 дня] — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода). Формально говоря: если существует положительное число T>0, такое что на всей области определения функции выполняется равенство f(x)=f(x+T). Наименьшее из этих чисел называется периодом функции.
Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол , тангенс которого равен k : tan = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3 .
2.
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
3.
Обратная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина.
График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью ( о конических сечениях см. раздел «Конус» в главе «Стереометрия» ). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
Основные характеристики и свойства гиперболы:
- область определения функции: x 0, область значений: y 0 ;
- функция монотонная ( убывающая ) при x < 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
4.
Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a 0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её ершина лежит не в начале координат, а в точке с координатами:
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x2 и дискриминанта D = b2 – 4ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.
Изобразите, пожалуйста, квадратную параболу для случая a > 0, D > 0 .
Основные характеристики и свойства квадратной параболы:
- область определения функции: - < x < + ( т.e. x R ), а область
значений: … (ответьте, пожалуйста, на этот вопрос сами !);
- функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0,
и непериодическая;
- при D < 0 не имеет нулей. ( А что при D 0 ? ) .
5.
Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 - квадратную параболу ; при n = -1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степенной функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, приn = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат ( поясните, пожалуйста, почему ? ). Все эти случаи ( при a = 1 ) показаны на рис.13 ( n 0 ) и рис.14 ( n < 0 ). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции:
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой.
На рис.16 представлена функция . Эта функция является обратной к квадратной параболе y = x 2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.
6.
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.
Основные характеристики и свойства показательной функции:
- область определения функции: - < x < + ( т.e. x R );
область значений: y > 0 ;
- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.
7.
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции:
- область определения функции: x > 0, а область значений: - < y < +
( т.e. y R );
- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
8.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на /2.
Из этих графиков очевидны характеристики и свойства этих функций:
- область определения: - < x < + ; область значений: -1 y +1;
- эти функции периодические: их период 2 ;
- функции ограниченные ( | y | 1 ), всюду непрерывные, не монотонные, но
имеющие так называемые интервалы монотонности, внутри которых они
ведут себя, как монотонные функции ( см. графики рис.19 и рис.20 );
- функции имеют бесчисленное множество нулей (подробнее см. раздел
«Тригонометрические уравнения»).
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Из графиков видно, что эти функции: периодические (их период ), неограниченные, в целом не монотонные, но имеют интервалы монотонности (какие?), разрывные (какие точки разрыва имеют эти функции?).
Область определения и область значений этих функций:
9.
Обратные тригонометрические функции. Определения обратных тригонометрических функций и их основные свойства приведены в одноимённом разделе в главе «Тригонометрия». Поэтому здесь мы ограничимся лишь короткими комметариями, касающимися их графиков, полученных поворотом графиков тригонометрических функций вокруг биссектрисы 1-го координатного угла.
Функции y = Arcsin x ( рис.23 ) и y = Arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно: -1 x +1 и - < y < + . Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: -1 x +1 ;
их области значений: -/2 y /2 для y = arcsin x и 0 y для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x).
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 ) - многозначные, неограниченные; их область определения: - x + . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: - x + ;
их области значений: -/2 < y < /2 для y = arctan x и 0 < y < для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 );
функция y = arccot x нулей не имеет.
В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой
| Предел функции в точке |
1. Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство | f(x) – a | < e .
Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {xn}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n хn ≠ а, последовательность {yn = f(xn)} сходится к b.
Данные определения предполагают, что функция у = f(x) определена в некоторой окрестноститочки а, кроме, быть может, самой точки а.
Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.
Указанный предел обозначается так:
 Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике
Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике
|
| Предел функции на бесконечности |
Предел функции на бесконечности.Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:
 Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:
Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так:
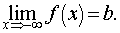
|
Раскрытие неопределённостей
Материал из Википедии — свободной энциклопедии
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

| 
| 
| 
| 
| 
| 
|
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов  ,
,  ,
,  пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.



Для раскрытия неопределённостей типа  используется следующий алгоритм:
используется следующий алгоритм:
- Выявление старшей степени переменной;
- Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа  существует следующий алгоритм:
существует следующий алгоритм:
- Разложение на множители числителя и знаменателя;
- Сокращение дроби.
Для раскрытия неопределённостей типа  иногда удобно применить следующее преобразование:
иногда удобно применить следующее преобразование:
Пусть  и
и 

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Аси́мпто́та[1] (от греч. ασϋμπτωτος — несовпадающий, не касающийся) кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность[2]. Термин впервые появился у Аполлония Пергского, хотя асимптоты гиперболы исследовал ещёАрхимед[3].
Нахождение асимптот
[править]Порядок нахождения асимптот
- Нахождение вертикальных асимптот.
- Нахождение двух пределов

- Нахождение двух пределов
 :
:
если  в п. 2.), то
в п. 2.), то  , и предел
, и предел  ищется по формуле горизонтальной асимптоты,
ищется по формуле горизонтальной асимптоты,  .
.
[править]Наклонная асимптота — выделение целой части
Дана функция  .
.
Разделив нацело числитель на знаменатель, получим:
 .
.
При  ,
,  , то есть:
, то есть:
 ,
,
и  является искомым уравнением асимптоты.
является искомым уравнением асимптоты.
- Схема постраения графика
Найти ОДЗ и точки разрыва функции.- Найти точки пересечения графика функции с осями координат.
- Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
- Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
- Найти асимптоты графика функции: а) вертикальные, b) наклонные.
- На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
ПРОИЗВОДНАЯ
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Геометрический и физический смысл производной
[править]Тангенс угла наклона касательной прямой


Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точкиx0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Основная статья: Касательная прямая
Если функция  имеет конечную производную в точке
имеет конечную производную в точке  то в окрестности
то в окрестности  её можно приблизитьлинейной функцией
её можно приблизитьлинейной функцией

Функция  называется касательной к
называется касательной к  в точке
в точке  Число
Число  является угловым коэффициентом или тангенсом угла наклонакасательной прямой.
является угловым коэффициентом или тангенсом угла наклонакасательной прямой.
[править]Скорость изменения функции
Пусть  — закон прямолинейного движения. Тогда
— закон прямолинейного движения. Тогда  выражает мгновенную скорость движения в момент времени
выражает мгновенную скорость движения в момент времени  Вторая производная
Вторая производная  выражает мгновенное ускорение в момент времени
выражает мгновенное ускорение в момент времени 
Вообще производная функции  в точке
в точке  выражает скорость изменения функции в точке
выражает скорость изменения функции в точке  , то есть скорость протекания процесса, описанного зависимостью
, то есть скорость протекания процесса, описанного зависимостью 
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
-

-

-
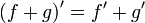 [2]
[2] -
 [3]
[3] -

-
 …(g ≠ 0)
…(g ≠ 0) -
 (g ≠ 0)
(g ≠ 0) - Если функция задана параметрически:
 , то
, то 
Основная статья: Дифференцирование сложной функции
-

- Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
 где
где  — биномиальные коэффициенты.
— биномиальные коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
- если функция дифференцируема на интервале
 , то она непрерывна на интервале
, то она непрерывна на интервале  . Обратное, вообще говоря, неверно (например, функция
. Обратное, вообще говоря, неверно (например, функция  на
на  );
); - если функция имеет локальный максимум/минимум при значении аргумента, равном
 , то
, то  (это так называемая лемма Ферма);
(это так называемая лемма Ферма); - производная данной функции единственна, но у разных функций могут быть одинаковые производные.
-

Функция 
| Производная 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
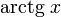
| 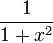
| |

| 
| |
Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f '(x) и f '(a).
4. Подставить найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) -f '(a)(x – a).
Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.
Практика показала, что последовательное решение каждой из ключевых задач при помощи алгоритма позволяет формировать умения написания уравнения касательной к графику функции поэтапно, а шаги алгоритма служат опорными пунктами действий. Данный подход соответствует теории поэтапного формирования умственных действий, разработанной П.Я. Гальпериным и Н.Ф. Талызиной [3].
Производные высших порядков
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция  дифференцируема в
дифференцируема в  , то производная первого порядка определяется соотношением
, то производная первого порядка определяется соотношением

Пусть теперь производная  -го порядка
-го порядка  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и дифференцируема. Тогда
и дифференцируема. Тогда

Если функция  имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от
имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от  может иметь в некоторой точке
может иметь в некоторой точке 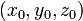 частные производные по той же или по любой другой переменной. Для исходной функции
частные производные по той же или по любой другой переменной. Для исходной функции  эти производные будут частными производными второго порядка (или вторыми частными производными).
эти производные будут частными производными второго порядка (или вторыми частными производными).
 или
или 
 или
или 
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

НЕОПРЕДЕЛЕННОСТИ
усть заданы две функции  и
и  . Если существуют
. Если существуют  и
и  , то существуют и пределы суммы и произведения этих функций, а при
, то существуют и пределы суммы и произведения этих функций, а при  и предел частного, причем
и предел частного, причем
 ,
,
 ,
,
 .
.
Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть  . Из приведенных формул следует полезное утверждение:
. Из приведенных формул следует полезное утверждение:
 , то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной
, то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной  , то вычисление предела при
, то вычисление предела при  всегда можно свести к вычислению предела при
всегда можно свести к вычислению предела при  . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке
. Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке  в выражение для функции.
в выражение для функции.
ПРИМЕР 1. Простейшие методы вычисления пределов
Неопределенности и их раскрытие.
Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если  и
и  , то может существовать
, то может существовать  . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа  . Также может существовать
. Также может существовать  , в этом случае имеем неопределенность типа
, в этом случае имеем неопределенность типа 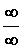 . Если
. Если  и
и  , то может существовать
, то может существовать  . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа  . Если
. Если  и
и  , то может существовать
, то может существовать  - неопределенность типа
- неопределенность типа 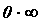 . Рассматривают также неопределенности типа
. Рассматривают также неопределенности типа 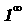 ,
,  и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой
и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой  в выражение для функции. Полезно запомнить замечательные пределы:
в выражение для функции. Полезно запомнить замечательные пределы:
 (е = 2.71828… - основание натуральных логарифмов) - неопределенность типа
(е = 2.71828… - основание натуральных логарифмов) - неопределенность типа 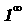 .
.
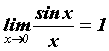 - неопределенность типа
- неопределенность типа  .
.
ПРИМЕР 2. Простейшие методы раскрытия неопределенностей
Использование эквивалентных бесконечно малых.
Если мы имеем неопределенность типа  , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке
, то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке  равен нулю. Пусть
равен нулю. Пусть  ,
,  ,
,  ,
,  - бесконечно малые функции при
- бесконечно малые функции при  , причем
, причем  эквивалентна
эквивалентна  , т.е.
, т.е.  ~
~  ,
,  ~
~  (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда
(напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда  , т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную.
, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную.
ПРИМЕР 3. Раскрытие неопределенностей с помощью эквивалентных бесконечно малых
Правило Лопиталя.
Неопределенности типа  или
или 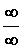 удобно раскрывать с помощью правила Лопиталя. Пусть
удобно раскрывать с помощью правила Лопиталя. Пусть  и
и  две бесконечно малые или бесконечно большие функции при
две бесконечно малые или бесконечно большие функции при  и существует предел отношения их производных при
и существует предел отношения их производных при  . Тогда
. Тогда  . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.
. Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.
ПРИМЕР 4. Раскрытие неопределенностей с помощью правила Лопиталя
Формула Тейлора.
Пусть функция  имеет в точке
имеет в точке  производные всех порядков до
производные всех порядков до  -го включительно. Тогда для
-го включительно. Тогда для  справедлива формула Тейлора:
справедлива формула Тейлора:


где  называется остаточным членом формулы Тейлора.
называется остаточным членом формулы Тейлора.
ПРИМЕР 5. Раскрытие неопределенностей с помощью формулы Тейлора
Точка x0называется точкой локального максимума функции f x, если существует такаяокрестность точки x0, что для всех x из этой окрестности f x f x 0.
Определение. Точка x0называется точкой локального минимума функции f x, если существует такаяокрестность точки x0, что для всех x из этой окрестности f x f x 0
ИНТЕГРАЛЫ
Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Неопределённый интегра́л для функции  — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Таблица основных неопределённых интегралов













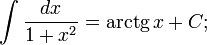


Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [a;b]. При выводе свойств будем использовать определение интеграла и формулу Ньютона-Лейбница.
1. Если с — постоянное число и функция ƒ(х) интегрируема на [a;b], то

т. е. постоянный множитель с можно выносить за знак определенного интеграла.
▼Составим интегральную сумму для функции с • ƒ(х). Имеем:

Тогда Отсюда вытекает, что функция  с • ƒ(х) интегрируема на [а; b] и справедлива формула (38.1).▲
с • ƒ(х) интегрируема на [а; b] и справедлива формула (38.1).▲
2. Если функции ƒ1(х) и ƒ2(х) интегрируемы на [а;b], тогда интегрируема на [а; b] их сумма u

т. е. интеграл от суммы равен сумме интегралов.
▼  ▲
▲
Свойство 2 распространяется на сумму любого конечного числа слагаемых.
3. 
Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница.

4. Если функция ƒ(х) интегрируема на [а; b] и а < с < b, то

т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
При разбиении отрезка [а;b] на части включим точку с в число точек деления (это можно сделать ввиду независимости предела интегральной суммы от способа разбиения отрезка [а; b] на части). Если с = хm, то интегральную сумму можно разбить на две суммы:

Каждая из написанных сумм является интегральной соответственно для отрезков [а; b], [а; с] и [с; b]. Переходя к пределу в последнем равенстве при n → ∞ (λ → 0), получим равенство (38.3).
Свойство 4 справедливо при любом расположении точек а, b, с (считаем, что функция ƒ (х) интегрируема на большем из получающихся отрезков).
Так, например, если а < b < с, то

Отсюда

(использованы свойства 4 и 3).
5. «Теорема о среднем». Если функция ƒ(х) непрерывна на отрезке [а; b], то существует тонка с є [а; b] такая, что

▼По формуле Ньютона-Лейбница имеем

где F'(x) = ƒ(х). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим
F(b)-F(a) = F'(c)•(b-а) = ƒ(с)•(b-а).▲
 Свойство 5 («теорема о среднем») при ƒ (х) ≥ 0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором с є (а; b), площади прямоугольника с высотой ƒ (с) и основанием b- а (см. рис. 170). Число
Свойство 5 («теорема о среднем») при ƒ (х) ≥ 0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором с є (а; b), площади прямоугольника с высотой ƒ (с) и основанием b- а (см. рис. 170). Число