 |
|
Ряды Тейлора и их приложения
1°. Если функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 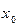 и имеет в этой точке производные всех порядков, то степенной ряд:
и имеет в этой точке производные всех порядков, то степенной ряд:
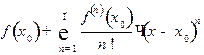
называют рядом Тейлора функции  в точке
в точке 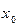 .
.
Если 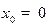 , то ряд
, то ряд

называют рядом Маклорена.
2°. Если функция  представлена степенным рядом:
представлена степенным рядом:
 ,
,  , то
, то
она бесконечно дифференцируема в окрестности точки 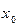 и равна сумме своего ряда Тейлора, коэффициенты степенного ряда равны коэффициентам ряда Тейлора:
и равна сумме своего ряда Тейлора, коэффициенты степенного ряда равны коэффициентам ряда Тейлора:
 ,
,  ,
,  .
.
Обратное утверждение неверно: существуют функции, бесконечно дифференцируемые в окрестности точки 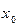 , ряд Тейлора которых не сходится при
, ряд Тейлора которых не сходится при  к функции
к функции  . Примером такой функции является:
. Примером такой функции является:

Можно показать, что существуют все производные  в точке
в точке  и они равны нулю. Сумма ряда Тейлора этой функции совпадает со значением этой функции только в точке
и они равны нулю. Сумма ряда Тейлора этой функции совпадает со значением этой функции только в точке  .
.
3°. Теорема (достаточный признак разложимости функции в ряд Тейлора).Если функция  и все ее производные ограничены в совокупности на некотором интервале
и все ее производные ограничены в совокупности на некотором интервале 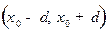 , то есть существует такая постоянная
, то есть существует такая постоянная 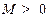 , что
, что 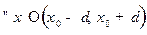 выполняется неравенство
выполняется неравенство 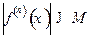
 , то функция
, то функция  представляется в каждой точке
представляется в каждой точке  сходящимся к ней рядом Тейлора:
сходящимся к ней рядом Тейлора:
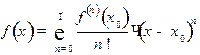 .
.
Доказательство этой теоремы основано на том, что при перечисленных условиях остаток ряда Тейлора  при
при  равномерно стремится к нулю на множестве
равномерно стремится к нулю на множестве  .
.
4°. Условия теоремы пункта 3º выполняются для функций
 ,
,  ,
,  ,
,  ,
, 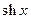 на любом промежутке
на любом промежутке  , поэтому справедливо разложение в ряд Тейлора для:
, поэтому справедливо разложение в ряд Тейлора для:
1) показательной функции:
 ,
,  ; (4)
; (4)
2) тригонометрических функций:
 ,
,  ; (5)
; (5)
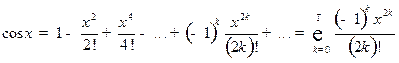 ,
,  ; (6)
; (6)
3) гиперболических функций:
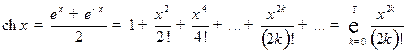 ,
,  ; (7)
; (7)
 ,
,  . (8)
. (8)
Радиус сходимости ряда Тейлора для функции  равен единице:
равен единице:
 , (9)
, (9)
где
 ,
,  ,
,  ,
,  .
.
В отдельных случаях для разложения функции в ряд Тейлора можно использовать уже известные результаты:
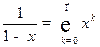 ,
,  ; (10)
; (10)
 ,
,  ; (11)
; (11)
 ,
,  . (12)
. (12)
(в разложении (11) 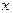 заменено на
заменено на 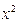 ).
).
Ряд Тейлора логарифмической функции может быть получен
почленным интегрированием разложений (10) и (11):
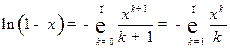 ,
,  ; (13)
; (13)
 ,
,  . (14)
. (14)
Интегрируя почленно ряд (12), можно получить разложение  :
:
 ; (15)
; (15)
Дифференцируя почленно ряд (10), получим:
 ,
,  . (16)
. (16)
Если в разложении (9) изменить 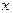 на
на 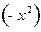 , а
, а  выбрать равным
выбрать равным  , то можем получить разложение:
, то можем получить разложение:
 ,
,  . (17)
. (17)
5°. Коэффициенты ряда Тейлора обычно находят с помощью известных разложений ((4)-(17)), применяя различные приемы: представление функции в виде суммы более простых функций, замену переменной, почленное интегрирование и дифференцирование ряда, метод неопределенных коэффициентов и прочие.
Примеры
Разложите в ряд Тейлора функции в заданной точке 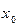 . Найдите радиус сходимости.
. Найдите радиус сходимости.
1. 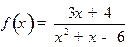 ,
, 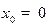 .
.
2.  ,
,  .
.
3.  ,
,  .
.
4. 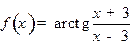 ,
, 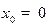 .
.
Решение
1. Представим рациональную функцию в виде суммы элементарных рациональных дробей:


 .
.
Используя разложения (10) и (11), получим:
 ,
, 

 ;
;
 ,
, 

 .
.
Окончательно:
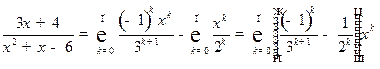 ,
,
где  .
.
2. В этом случае нужно разложить функцию в окрестности точки  , то есть по степенями
, то есть по степенями  . Полагая
. Полагая  , получим:
, получим:
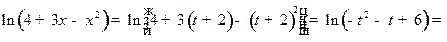
 .
.
Используя формулы (13) и (14), находим:
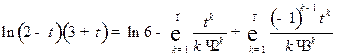 ,
,  .
.
Отсюда окончательно получим:
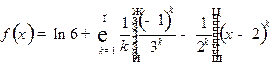 ,
,  .
.
3. Поскольку  :
:

 .
.
Обозначим  ,
,  , тогда:
, тогда:
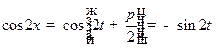 ,
,
 .
.
И поэтому:
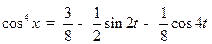 .
.
Используя формулы (5) и (6), получим:

 ,
,  .
.
4. Вычислим производную заданной функции 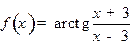 ,
,
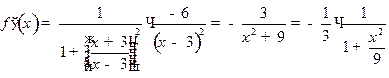 .
.
Из разложения (12) следует, что
 ,
,  .
.
Интегрируя полученный ряд почленно, получаем:
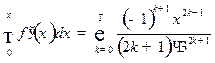 ,
,  ,
,
 .
.
Окончательно имеем:
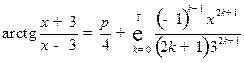 ,
,  .
.
6°. Ряды Тейлора часто используют для вычисления сумм числовых рядов, интегралов, вычисления приближенных значений функций, интегралов, решения дифференциальных уравнений.
Примеры
1. Вычислите  .
.
2. Вычислите интеграл  с точностью до
с точностью до  .
.
3. Вычислите с точностью до  .
.
 ,
,  .
.
4. Найдите решение уравнения  , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  .
.
Решение
1. Используя разложение:
 ,
,  , получим:
, получим:
 .
.
Отсюда находим:
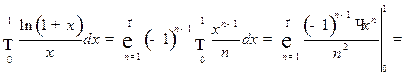


 .
.
2. Преобразуем подынтегральную функцию

и в исходном интеграле сделаем замену переменной:

 .
.
Раскладывая теперь в ряд Маклорена функцию:
 ,
,
получим:



Если сохранить только два члена, то погрешность не будет превышать  .
.
Таким образом:
 ,
,  .
.
3. Запишем ряд Маклорена для функции  :
:
 ,
,  .
.
Для  это равенство примет вид:
это равенство примет вид:
 ,
,
 .
.
4. Будем искать решение уравнения в виде степенного ряда:
 .
.
Тогда
 ,
,
 .
.
Уравнение  примет вид:
примет вид:
 .
.
Приравнивая коэффициенты при одинаковых степенях 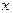 , получим:
, получим:
 ,
,  ,
,  .
.
Так как  , то согласно рекуррентному соотношению:
, то согласно рекуррентному соотношению:
 ,
, 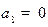 , ...,
, ..., 
 .
.
Из этого же соотношения:
 ,
,
 .
.
Поскольку
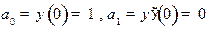 ,
,
то решение уравнения 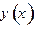 принимает вид:
принимает вид:
