 |
|
Амплитудная модуляция
При амплитудной модуляции амплитуда несущего колебания изменяется по закону управляющего, модулирующего колебания.
Для простоты рассмотрим случай модуляцию одним тоном, когда сигнал сообщения представляет собой низкочастотное гармоническое колебание 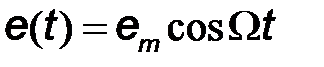 . Частота несущего колебания выбирается как минимум на порядок выше частоты сигнала сообщения
. Частота несущего колебания выбирается как минимум на порядок выше частоты сигнала сообщения  . Не нарушая общности, начальную фазу несущего гармонического колебания будем считать равной нулю
. Не нарушая общности, начальную фазу несущего гармонического колебания будем считать равной нулю  . Тогда амплитудно-модулированный (АМ) сигнал описывается выражением
. Тогда амплитудно-модулированный (АМ) сигнал описывается выражением
 , (7.9)
, (7.9)
где  – коэффициент модуляции амплитуды.
– коэффициент модуляции амплитуды.
Из (7.9) видим, что амплитудно модулированный сигнал получают в процессе перемножения высокочастотного и низкочастотного колебаний.
Найдем спектр амплитудно-модулированного сигнала. Для этого в (7.9) выполним преобразования
 (7.10)
(7.10)
Из (7.10) видим, что в процессе модуляции происходит изменение спектрального состава высокочастотного сигнала. Спектр АМ сигнала содержит три частоты (см. рис. 7.3): несущую частоту  и две боковые частоты. Информация о модулирующем колебании запечатлевается в амплитудах двух колебаний, частоты которых называются нижней боковой частотой
и две боковые частоты. Информация о модулирующем колебании запечатлевается в амплитудах двух колебаний, частоты которых называются нижней боковой частотой  и верхней боковой частотой
и верхней боковой частотой  . Амплитуды колебаний боковых частот одинаковы и равны
. Амплитуды колебаний боковых частот одинаковы и равны  .
.
Рис. 7.3. Спектральная диаграмма сигнала амплитудно-модулированного одним тоном
Если модулирующий сигнал занимает полосу частот, ограниченную частотами  и
и 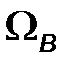 , то в спектре АМ сигнала кроме несущего колебания будут еще две боковые полосы: нижняя боковая частота (от
, то в спектре АМ сигнала кроме несущего колебания будут еще две боковые полосы: нижняя боковая частота (от  до
до  ) и верхняя боковая частота (от
) и верхняя боковая частота (от  до
до  ).
).
Устройства, в которых осуществляется модуляция высокочастотного несущего колебания, называются модуляторами.
Работа амплитудных модуляторов основана на перемножении несущего и модулирующего колебаний на нелинейном элементе. ВАХ нелинейного элемента (диода, транзистора) можно аппроксимировать полиномом
 . (7.11)
. (7.11)
Напряжение, поданное на вход нелинейного элемента, представим в виде  . При прохождении тока через нелинейную цепь в его спектре кроме частот несущего и модулирующего колебания появляются комбинационные частоты:
. При прохождении тока через нелинейную цепь в его спектре кроме частот несущего и модулирующего колебания появляются комбинационные частоты:
 (7.12)
(7.12)
С помощью полосового фильтра, например, колебательного контура с добротностью 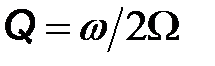 из спектра тока можно выделить компоненты с частотами близкими к частоте несущего колебания
из спектра тока можно выделить компоненты с частотами близкими к частоте несущего колебания
 . (7.13)
. (7.13)
Из сравнения (7.13) с (7.10) видно, что ток содержит те же частотные составляющие, что и напряжение  сигнала с амплитудной модуляцией одной гармоникой. На рис. 7.4а показана схема АМ модулятора, в котором осуществляется базовая модуляция. На рис. 7.4б приведено графическое объяснение процесса модуляции с использованием кусочно-линейной аппроксимации проходной вольт-амперной характеристики биполярного транзистора. Из рис. 7.4б видно, что НЧ модулирующий сигнал управляет положением рабочей точки условного режима покоя (при отсутствии ВЧ несущего колебания)
сигнала с амплитудной модуляцией одной гармоникой. На рис. 7.4а показана схема АМ модулятора, в котором осуществляется базовая модуляция. На рис. 7.4б приведено графическое объяснение процесса модуляции с использованием кусочно-линейной аппроксимации проходной вольт-амперной характеристики биполярного транзистора. Из рис. 7.4б видно, что НЧ модулирующий сигнал управляет положением рабочей точки условного режима покоя (при отсутствии ВЧ несущего колебания) 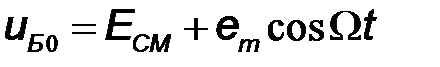 . В результате этого производится управление коллекторным током, который возбуждает в колебательном контуре, являющемся нагрузкой ЭП, высокочастотные колебания. Амплитуда напряжения на выходе модулятора повторяет изменения амплитуды напряжения на контуре.
. В результате этого производится управление коллекторным током, который возбуждает в колебательном контуре, являющемся нагрузкой ЭП, высокочастотные колебания. Амплитуда напряжения на выходе модулятора повторяет изменения амплитуды напряжения на контуре.
Угловая модуляция
В зависимости от того, каким параметром высокочастотного колебания 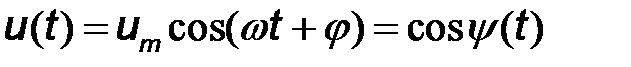 управляет низкочастотное колебание, различают частотную и фазовую модуляцию.
управляет низкочастотное колебание, различают частотную и фазовую модуляцию.
При частотной модуляции частота является функцией 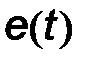 :
:
 , (7.14)
, (7.14)
где  – частота несущего колебания,
– частота несущего колебания,  – коэффициент.
– коэффициент.
Поскольку частота  – это скорость изменения фазового угла
– это скорость изменения фазового угла  , то частотно модулированный сигнал в общем виде можно представить как
, то частотно модулированный сигнал в общем виде можно представить как
 . (7.15)
. (7.15)

а)

б)
Рис. 6.4. Амплитудный модулятор
а) схема модулятора, в котором осуществляется базовая амплитудная модуляция;
б) графическое объяснение процесса модуляции
При фазовой модуляции функцией  является фаза
является фаза  . При этом сигнал с фазовой модуляцией в общем случае примет виде:
. При этом сигнал с фазовой модуляцией в общем случае примет виде:
 . (7.16)
. (7.16)
Рассматривая мгновенное значение частоты как скорость изменения фазового угла  , получим:
, получим:
 . (7.17)
. (7.17)
Из приведенных выражений (7.14) – (7.17) видим, что как при частотной, так и при фазовой модуляции происходит изменение и частоты, и фазы, а в результате и фазового угла  . Поэтому эти два вида модуляции рассматривают как угловую модуляцию.
. Поэтому эти два вида модуляции рассматривают как угловую модуляцию.
В случае частотной модуляции одним тоном управляющего низкочастотного сигнала  мгновенное значение частоты имеет вид
мгновенное значение частоты имеет вид
 , (7.18)
, (7.18)
где  – максимальное отклонение значения частоты от несущей частоты
– максимальное отклонение значения частоты от несущей частоты 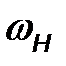 , которое называют девиацией частоты.
, которое называют девиацией частоты.
После выполнения в (7.15) интегрирования высокочастотный сигнал, частотно модулированный одним тоном, запишем как
 . (7.19)
. (7.19)
Здесь параметр  характеризует максимальное отклонение фазы и называется индексом модуляции.
характеризует максимальное отклонение фазы и называется индексом модуляции.
Отметим, что при фазовой модуляции одним тоном индекс модуляции  , а девиация частоты
, а девиация частоты 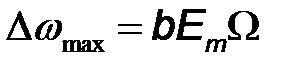 .
.
Рассмотрим амплитудный спектр высокочастотного ЧМ сигнала, модулированного одним тоном. Для этого преобразуем (7.19)
 (7.20)
(7.20)
Из теории специальных функций известно, что  и
и  можно представить в виде
можно представить в виде
 (7.21)
(7.21)
Подставив (7.21) в (7.20) можно видеть, что спектр модулированного одним тоном ЧМ сигнала содержит бесконечный набор гармоник. Однако вкладом в амплитудный спектр гармоник с номерами  можно пренебречь, поскольку значения функций Бесселя
можно пренебречь, поскольку значения функций Бесселя  становятся очень малыми (см. рис. 7.5, на котором показаны функции Бесселя порядка
становятся очень малыми (см. рис. 7.5, на котором показаны функции Бесселя порядка  =0, 1, 2)..
=0, 1, 2)..
В виду этого, ширину спектра ЧМ сигнала при больших индексах модуляции (  ) принимают равной
) принимают равной
 , (7.22)
, (7.22)
т.е. ширина спектра равна удвоенной девиации частоты
Следует также отметить, что при индексах модуляции ( 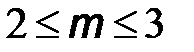 ) становится подавленной амплитуда несущего колебания. Это способствует тому, что основная часть мощности передатчика ЧМ сигнала сосредоточена в боковых полосах спектра, несущих информацию.
) становится подавленной амплитуда несущего колебания. Это способствует тому, что основная часть мощности передатчика ЧМ сигнала сосредоточена в боковых полосах спектра, несущих информацию.
Частотную модуляцию наиболее просто можно осуществить, управляя частотой высокочастотного колебания автогенератора, путем перестройки колебательного контура с помощью варикапа. Вариант схемы частотного модулятора с варикапом на основе  – автогенератора (емкостная трехточка), представлен на рис. 7.6а. Варикап, подключенный параллельно колебательному контуру, управляет его резонансной частотой
– автогенератора (емкостная трехточка), представлен на рис. 7.6а. Варикап, подключенный параллельно колебательному контуру, управляет его резонансной частотой 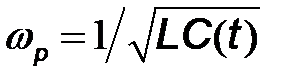 и, следовательно, частотой высокочастотных колебаний автогенератора.
и, следовательно, частотой высокочастотных колебаний автогенератора.
Известно, что барьерная емкость варикапа (обратно смещенного  -перехода) существенно зависит от приложенного напряжения и определяется вольт-фарадной характеристикой
-перехода) существенно зависит от приложенного напряжения и определяется вольт-фарадной характеристикой  (рис. 7.6б).
(рис. 7.6б).
В режиме покоя (модулирующий сигнал отключен) емкость варикапа  определяется напряжением смещения
определяется напряжением смещения  . Если точку покоя выбрать в линейной области вольт-фарадной характеристики варикапа, то емкость варикапа
. Если точку покоя выбрать в линейной области вольт-фарадной характеристики варикапа, то емкость варикапа 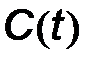 будет изменяться во времени относительно
будет изменяться во времени относительно  по закону, действующего на входе автогенератора модулирующего сигнала. Например, если
по закону, действующего на входе автогенератора модулирующего сигнала. Например, если  , то
, то  и тогда при
и тогда при 

 . (7.23)
. (7.23)
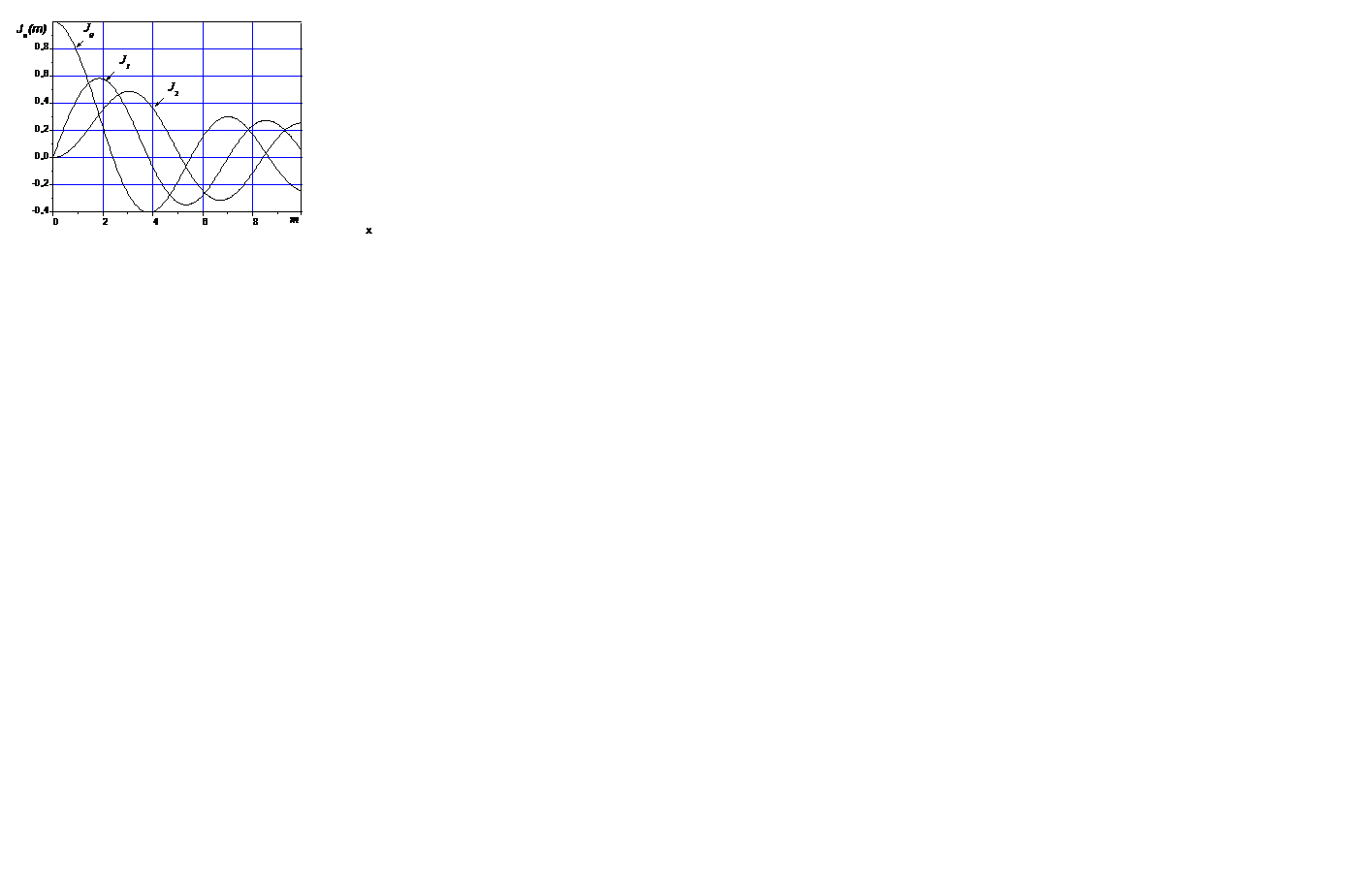
Рис. 7.5 Функции Бесселя порядка  =0, 1, 2
=0, 1, 2


а) б)
Рис. 7.6. Частотный модулятор
а) схема частотного модулятора с варикапом;
б) вольт-фарадная характеристика варикапа и временные диаграммы, поясняющие изменение его емкости