Главная | Обратная связь

Метод половинного деления

Входная информация: отрезок [a;b] с корнем непрерывной функции f(x) внутри и точность определения корня ε.

Исходный отрезок делится пополам точкой = 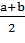и если f( )=0, то x – корень уравнения. Если f( )≠0, то из двух получившихся отрезков [a; ] и [ ;b] выбирается тот, на концах которого функция имеет противоположные знаки. (Например, если f(a) ∙ f( )<0, то выбирается [a; ]; если нет, то [ ;b]). Продолжаем процедуру деления до тех пор, пока |a-b|< ε. Тогда последнее значение будет искомым корнем с точностью ε. Этот метод всегда сходится к корню, но требуется большое количество приближений n, которое можно определить из соотношения ε ∙ = |b-a| (так при |b-a|=1 и ε=0.001, n=10).

Pascal

 

Пакет Excel

 

Пакет MathCAD

Метод последовательных приближений

Исходное уравнение F(x) = x+ + -2.5 преобразуем к виду x = φ(x). Если на рассматриваемом интервале изоляции корня [0.7; 0,8] |φ’(x)|<1, то расчетная формула примет вид : =φ( ), и при этом итерационный процесс приближения к корню будет сходящимся.

В нашем случае непосредственный выбор расчетной формулы вызывает затруднения. Поэтому воспользуемся следующим приемом.

Введем в рассмотрение произвольный параметр λ>0 . Тогда функцию φ(x) можно представить как φ(x) = x - λ∙F(x). Затем, варьируя параметр λ, добиваемся условия сходимости: |φ’(x)|<1 на [a; b]. φ’(x)=1-λ∙F’(x). Для выполнения сходимости λ= на [a; b].

Для рассматриваемого примера:

max|F’(x)| на (a; b) = max| (1 + + 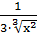)|= 2 (при x=0.7). λ = .

Расчетная формула метода итерации примет вид:

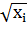= - ∙( + + -2.5) = .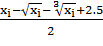

Блок-схема

Pascal

Пакет Excel

Пакет MathCAD

Метод Ньютона

Этот метод можно рассматривать как частный случай метода простой итерации с рекуррентной формулой = – и тем же принципом выбора начального приближения .

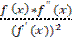Последовательность является сходящейся, ибо (x) = и (x)=0. Что означает, что если выбрано из малой окрестности корня, то (x)≤1. При произвольном итерации будут сходиться, если всюду

|f (x) * | < .

Геометрически метод Ньютона соответствуют последовательному проведению касательных к кривой y = f(x) в точках ( ; f ( )) и выборе в качестве нового приближения точки пересечения их с осью абсцисс.

Для рассматриваемого нами примера (F(x) = x+ + -2.5) первая производная равна F‘(x)=1+ + , а вторая производная имеет вид

F’’(x) = - - . Итерационная формула примет вид:

= - .

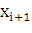В качестве начального приближения берется тот конец интервала изоляции, на котором функция и ее вторая производная имеют одинаковые знаки. Найдем значения функции на концах отрезка [0,7; 0,8]:

F(0,7)=0.7+ + -2.5≈ -0,075<0;

F’’(0.7)= - - ≈-0,6282<0.

Таким образом, за начальное приближение примем =0.7.

Процесс итераций идет до тех пор, пока |F( |<ε. В случае неудачного выбора рекуррентной формулы получается расходящийся процесс, и условие сравнения с точностью не достигается. Для исключения подобной ситуации введем счетчик итерации n, увеличивающийся каждый раз на единицу, и поставим искусственное условие продолжения итерации в случае n<=k. В противном случае завершим алгоритм с выводом текстового сообщения о невозможности получения корня за заданное количество k шагов.

 

Блок-схема

 

 

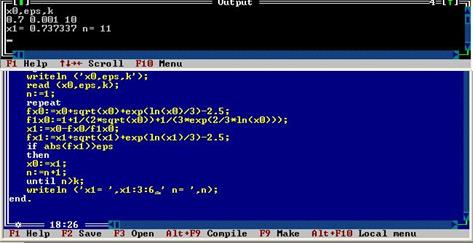Pascal

 

Пакет Excel

 

Пакет MathCAD

4.

Анализ результатов

Как видно из выше представленной таблицы более точные результаты корня x в средах Excel и Pascal, хотя сам процесс уточнения был более прост и быстр в среде MathCAD. В среде MathCAD уже заложены специальные формулы, которые позволяют найти более точное значение уже со второго приближения. В среде Pascal к примеру в методе последовательных приближений потребовалось 10 приближений, а в методе Ньютона число приближений равняется 11. Уточнение корня напрямую зависит от точности его нахождения , чем меньше, тем точнее будет корень.

Заключение

В данной работе рассмотрена только одна из большого количества задач численного решения. Аналогичным образом могут быть решены и другие задачи:

· погрешность результатов численного решения задач;

· решение задач линейной алгебры;

· решение задачи аппроксимации функций;

· решение задачи численного вычисления определенных интегралов;

· приближенное решение обыкновенных дифференциальных уравнений;

· решение задач одномерной и многомерной оптимизации и др.

Варианты заданий

№ Задания	Уравнение

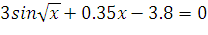
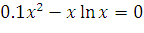
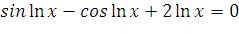
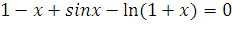
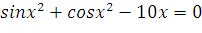
Список рекомендуемой литературы

1. Бахтиярова Л.Н. Microsoft Office 2007 Часть 1. Учебно-методическое пособие. – Н.Новгород: ВГИПУ.2008. – 133c.

2. Груздева М.Л., Червова А.А.Экономические и инженерные расчёты в среде MathCad. Учебное пособие. – Н.Новгород: ВГИПУ. – 2007. – 90с.

3. Ершов В.Н. Численные методы. Учебно-методическое пособие. – Н.Новгород: ВГИПУ. – 2009. – 49с.