 |
|
Тема 6. Неявные функции.
1.1. Функция, заданная таким способом: y=f(x) [или y=f(x1, x2,…,xm)] называется неявной ф-ей и является решением уравнения F(x,y)=0 [или F(x1, x2,…,xm,y)=0]относительно у (т.е.  [или F(x1, x2,…,xm, f(x1, x2,…,xm))=0])
[или F(x1, x2,…,xm, f(x1, x2,…,xm))=0])
1.2.
1.3. Функции  называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция
называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция  называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде:
называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде: 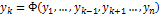 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
1.4. Функции  называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция
называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция  называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде:
называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде: 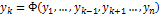 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
2.1. Теорема о существовании и непрерывности ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть 1) ф-я F(x,y) непрерывна в прямоугольнике Q={(x,y):a<x<b, c  }; 2)
}; 2)  (т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)
(т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)  ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
2.2. Теорема о дифференцируемости ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть: 1)ф-я F(x,y) дифференцируема в некоторой окрестности W точки Мо(х0,у0); 2) частная производная Fy непрерывна в точке Мо; 3)F(x0,y0)=0,  Тогда существует такой прямоугольник
Тогда существует такой прямоугольник  , в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (
, в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (  и ее производная вычисляется по формуле
и ее производная вычисляется по формуле  .
.
2.3.
2.4.
2.5. Теорема о существовании и дифференцируемости ф-ий y и z, заданных неявно сисемой. Пусть 1)ф-ии F и G, входящие в систему, дифференцируемы в некоторой окрестности W точки 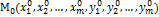 ; 2) частные производные
; 2) частные производные  непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,
непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,  Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  , в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при
, в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при 
2.6. Теорема о достаточных условиях независимости ф-ии.
Пусть ф-ии  , где n
, где n  m, дифференцируемы в некоторой окрестности
m, дифференцируемы в некоторой окрестности  точки
точки  и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в
и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в  .
.
2.7. Теорема о зависимости и независимости ф-ий.
Пусть: 1) ф-ии  дифференцируемы в окрестности
дифференцируемы в окрестности  точки
точки  , а частные производные
, а частные производные  непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий
непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий  ) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
Тогда r ф-ий, представленных в указанном миноре r-го порядка, независимы в w, а каждая из остальных ф-ий зависит в некоторой окрестности т. М0 от этих r ф-ий.
Тема 8. Кратные интегралы.
1.1. Плоская фигура называется квадрируемой, если точная верхняя грань 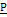 множества площадей всех вписанных многоугольных фигур равна точной нижней грани
множества площадей всех вписанных многоугольных фигур равна точной нижней грани  множества площадей всех описанных многоугольных фигур.
множества площадей всех описанных многоугольных фигур.
1.2. Площадь криволинейной трапеции.  , [ограничена непрерывными кривыми y=f1(x), y=f2(x), a
, [ограничена непрерывными кривыми y=f1(x), y=f2(x), a  (где
(где  , и двумя отрезками прямых х=а, x=b.]
, и двумя отрезками прямых х=а, x=b.]
1.3. Сумма  называется интегральной суммой ф-ии f(x,y), где G – квадрируемая область; u=f(M)=f(x,y) – ограниченная ф-я, определенная на G; Gi (i=
называется интегральной суммой ф-ии f(x,y), где G – квадрируемая область; u=f(M)=f(x,y) – ограниченная ф-я, определенная на G; Gi (i=  ) – разбиение области G, такое что 2 любые части не имеют общих внутренних точек;
) – разбиение области G, такое что 2 любые части не имеют общих внутренних точек;  – произвольная точка в Gi.
– произвольная точка в Gi.
1.4. Число I называется пределом интегральных сумм  при d -> 0, если
при d -> 0, если  такое, что для любого разбиения области G, у которого d<
такое, что для любого разбиения области G, у которого d<  , и для любого выбора промежуточных точек Mi выполняется неравенство |
, и для любого выбора промежуточных точек Mi выполняется неравенство |  .
.
2.1. Теорема о сведении двойного интеграла к повторному.
Пусть: 1)  двойной интеграл
двойной интеграл  ; 2)
; 2)  существует определенный интеграл
существует определенный интеграл  . Тогда существует определенный интеграл
. Тогда существует определенный интеграл  (он называется повторным)и справедливо равенство
(он называется повторным)и справедливо равенство 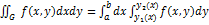 , т.е. двойной интеграл равен повторному.
, т.е. двойной интеграл равен повторному.
2.2. Теорема о формуле для замены переменной в двойном интеграле.
Пусть g и G – замкнутые квадрируемые области, функция f(x,y) ограничена в области G и непрерывна всюду, кроме, быть может, некоторого множества точек площади нуль, а отображение  удовлетворяет условиям :1)отображение взаимно однозначное; 2) ф-ии
удовлетворяет условиям :1)отображение взаимно однозначное; 2) ф-ии  и
и  имеют в области g непрерывные частные производные первого порядка; 3) якобиан отображения
имеют в области g непрерывные частные производные первого порядка; 3) якобиан отображения 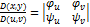 отличен от нуля во всех точках области g. Тогда справедливо равенство:
отличен от нуля во всех точках области g. Тогда справедливо равенство:  .
.
2.3. Теорема о сведении тройного интеграла к повторному.
Пусть 1) Существует тройной интеграл  2)
2)  существует определенный интеграл
существует определенный интеграл  . Тогда существует двойной интеграл
. Тогда существует двойной интеграл  (он называется повторным и справедливо равенство
(он называется повторным и справедливо равенство  , т.е. тройной интеграл равен повторному.
, т.е. тройной интеграл равен повторному.
2.4. Теорема о формуле замены переменных для тройного интеграла.
Пусть  и Т – замкнутые кубируемые области, ф-я f(x,y,z) ограничена в области Т и непрерывна всюду, кроме, быть может, некоторого множества точек объема 0, а отображение
и Т – замкнутые кубируемые области, ф-я f(x,y,z) ограничена в области Т и непрерывна всюду, кроме, быть может, некоторого множества точек объема 0, а отображение  удовлетворяет условиям: 1) отображение взаимнооднозначно; 2)ф-ии
удовлетворяет условиям: 1) отображение взаимнооднозначно; 2)ф-ии  имеют в области
имеют в области  непрерывные частные производные первого порядка; 3) Якобиан отображения
непрерывные частные производные первого порядка; 3) Якобиан отображения  отличен от 0 в области
отличен от 0 в области  . Тогда справедливо равенство:
. Тогда справедливо равенство: 
2.5. Масса и координаты центра тяжести. 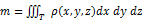 .
.  , где
, где  – плотность, Т – материальное тело.
– плотность, Т – материальное тело.
2.6. Моменты инерции плоской фигуры.

 - относительно координатных плоскостей Oyz, Ozx, Oxy.
- относительно координатных плоскостей Oyz, Ozx, Oxy.
 – относительно осей координат Ох, Оy, Oz.
– относительно осей координат Ох, Оy, Oz.
 - относительно начала координат.
- относительно начала координат.
4.1.
4.2.
Тема 7 Условный экстремум
1.1 Говорят, что функция  ,..,
,..,  имеет в точке
имеет в точке  условный минимум(максимум) при условиях связи
условный минимум(максимум) при условиях связи  , если существует такая окрестность точки
, если существует такая окрестность точки  что для любой точки
что для любой точки 
 этой окрестности, координаты которой удовлетворяют уравнениям
этой окрестности, координаты которой удовлетворяют уравнениям  , выполняется неравенство
, выполняется неравенство 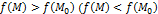 )
)
1.2 Задача об условном экстремуме функции  ,..,
,..,  при условиях связи
при условиях связи  эквивалентна задаче об условном экстремуме функции Лагранжа
эквивалентна задаче об условном экстремуме функции Лагранжа  (
(  при тех же условиях связи,поскольку в точке M, удовлетворяющих уравнениям связи, справедливо равенство Ф(M)=f(M).
при тех же условиях связи,поскольку в точке M, удовлетворяющих уравнениям связи, справедливо равенство Ф(M)=f(M).
2.1 Необходимые условия Лагранжа условного экстремума.
Пусть :1) Функция  ,..,
,..,  дифференцируема в точке
дифференцируема в точке  и имеет в этой точке условный экстремум при условиях связи
и имеет в этой точке условный экстремум при условиях связи  ;2) уравнения
;2) уравнения  удовлетворяют в некоторой окрестности точки
удовлетворяют в некоторой окрестности точки  условиям теоремы Теорема о дифференцируемости ф-ии z=f(x,y), заданной неявно ур-ем F(x,y,z)=0. Пусть: 1) функция F(
условиям теоремы Теорема о дифференцируемости ф-ии z=f(x,y), заданной неявно ур-ем F(x,y,z)=0. Пусть: 1) функция F(  =F(M) дифференцируема в некоторой окрестности W точки Mo(
=F(M) дифференцируема в некоторой окрестности W точки Mo(  2) частная производная Fy непрерывна в точке
2) частная производная Fy непрерывна в точке  ; 3) F(M0)=0,
; 3) F(M0)=0,  Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  в котором ур-е F(x,y,z)=0 определяет единственную неявную ф-ю y=f(
в котором ур-е F(x,y,z)=0 определяет единственную неявную ф-ю y=f(  , причем f(
, причем f(  , функция y=f(
, функция y=f(  дифференцируема при
дифференцируема при  и ее частные производные вычисляются по формуле
и ее частные производные вычисляются по формуле  . (i=1,2,…,m).
. (i=1,2,…,m).
Тогда существуют числа  , такие что все частные производные первого порядка функции Лагранжа равны нулю в точке
, такие что все частные производные первого порядка функции Лагранжа равны нулю в точке  .
.
1.1.
1.2.
1.3. Функции  называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция
называются зависимыми в области D, если одна из них (безразлично какая) зависит в области D от остальных функций. [Функция  называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде:
называется зависимой в области D от остальных функций из совокупности, если ее можно представить в виде: 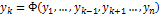 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
1.4. Функции  называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция
называются независимыми в области D, если ни одна из них не зависит в области D от остальных функций. [Функция  называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде:
называется независимой в области D от остальных функций из совокупности, если ее нельзя представить в виде: 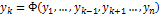 , где Ф – дифференциуемая ф-я своих аргументов]
, где Ф – дифференциуемая ф-я своих аргументов]
2.1. Теорема о существовании и непрерывности ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть 1) ф-я F(x,y) непрерывна в прямоугольнике Q={(x,y):a<x<b, c  }; 2)
}; 2)  (т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)
(т.е. на нижней и верхней сторонах прямоугольника Q ф-я F(x,y), имеет значения разных знаков); 3)  ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
ф-я F(x,y) является строго монотонной ф-ей аргумента у на сегменте [c,d]. Тогда на (a,b) существует единственная неявная ф-я, определяемая ур-ем F(x,y)=0, и эта ф-я непрерывна на (a,b).
2.2. Теорема о дифференцируемости ф-ии y=f(x), заданной неявно ур-ем F(x,y)=0. Пусть: 1)ф-я F(x,y) дифференцируема в некоторой окрестности W точки Мо(х0,у0); 2) частная производная Fy непрерывна в точке Мо; 3)F(x0,y0)=0,  Тогда существует такой прямоугольник
Тогда существует такой прямоугольник  , в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (
, в котором ур-е F(x,y)=0 определяет единсвенную неявную ф-ю вида y-f(x), причем f(x0)=y0, ф-я f(x) дифференцируема на интервале (  и ее производная вычисляется по формуле
и ее производная вычисляется по формуле  .
.
2.3.
2.4.
2.5. Теорема о существовании и дифференцируемости ф-ий y и z, заданных неявно сисемой. Пусть 1)ф-ии F и G, входящие в систему, дифференцируемы в некоторой окрестности W точки 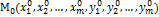 ; 2) частные производные
; 2) частные производные  непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,
непрерывны в точке Мо; 3)F(Mo)=0, G(Mo)=0,  Тогда существует такой параллелепипед
Тогда существует такой параллелепипед  , в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при
, в котором система уравнений определяет единственную совокупность неявных ф-ий, и эти ф-ии дифференцируемы при 
2.6. Теорема о достаточных условиях независимости ф-ии.
Пусть ф-ии  , где n
, где n  m, дифференцируемы в некоторой окрестности
m, дифференцируемы в некоторой окрестности  точки
точки  и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в
и пусть якобиан этих ф-ий по каким-либо переменным не равен 0 в точке М0. Тогда эти ф-ии независимы в  .
.
2.7. Теорема о зависимости и независимости ф-ий.
Пусть: 1) ф-ии  дифференцируемы в окрестности
дифференцируемы в окрестности  точки
точки  , а частные производные
, а частные производные  непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий
непрерывны в т М0; 2) функциональная матрица А (матрица из частных производных ф-ий  ) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
) имеет минор r-го порядка, неравный 0 в точке М0; 3) все миноры r+1 ранга матрицы А (если такие имеются) равны 0 в w.
Тогда r ф-ий, представленных в указанном миноре r-го порядка, независимы в w, а каждая из остальных ф-ий зависит в некоторой окрестности т. М0 от этих r ф-ий.
Тема 10 Поверхностные интегралы
1.1 Определение площади поверхностью.
Число S называется пределом сумм  при
при  , если
, если  такое, что для любого разбиения поверхности Ф , у которого d<
такое, что для любого разбиения поверхности Ф , у которого d<  , и для любого выбора точек
, и для любого выбора точек  выполняется неравенство |S(
выполняется неравенство |S(  . Если существует
. Если существует  , то поверхность Ф называется квадрируемой, а число S – площадью поверхности Ф.
, то поверхность Ф называется квадрируемой, а число S – площадью поверхности Ф.
1.2 Пусть на квадрируемой поверхности Ф определена функция  . Разобьем Ф кусочно гладкими кривыми на n квадрируемых частей. На каждой части
. Разобьем Ф кусочно гладкими кривыми на n квадрируемых частей. На каждой части  выберем произвольную точку
выберем произвольную точку  ,и составим интегральную сумму
,и составим интегральную сумму  , где
, где  . Пусть
. Пусть  .
.
Число  называется пределом интегральных сумм I(
называется пределом интегральных сумм I(  при
при  такое, что для любого разбиения Ф, у которого
такое, что для любого разбиения Ф, у которого  , и для любого выбора точек
, и для любого выбора точек  выполняется неравенство |(
выполняется неравенство |(  |<
|<  . Предел
. Предел  интегральных сумм называется поверхностным интегралом первого рода от функции
интегральных сумм называется поверхностным интегралом первого рода от функции  по поверхности Ф и называется
по поверхности Ф и называется  или
или 
1.3 Если поверхность ограничивает некоторое тело, то у него различают внешнюю и внутреннюю стороны. Примером такой поверхности является сфера. Если поверхность задача уравнением  , то у нее различают верхнюю и нижние стороны. Указанные поверхности имеют две стороны. Также существуют односторонние поверхности.
, то у нее различают верхнюю и нижние стороны. Указанные поверхности имеют две стороны. Также существуют односторонние поверхности.
Если каждой точке M области G поставлен в соответствие вектор a(M), то говорят, что в области G задано векторное поле. Векторное поле a(M)=  называется непрерывным в области G , если его координаты- функции
называется непрерывным в области G , если его координаты- функции  - являются непрерывными в области G. Гладкая поверхность Ф в каждой внутренней точке M имеет нормаль N(M), причем существует окрестность этой точки, вырезающая часть поверхности, на которой поле нормалей непрерывно. Если можно задать векторное поле нормалей, непрерывное на всей поверхности, то такая поверхность называется двусторонней. Поверхность, на которой не существует непрерывного вектора нормалей, называется односторонней.
- являются непрерывными в области G. Гладкая поверхность Ф в каждой внутренней точке M имеет нормаль N(M), причем существует окрестность этой точки, вырезающая часть поверхности, на которой поле нормалей непрерывно. Если можно задать векторное поле нормалей, непрерывное на всей поверхности, то такая поверхность называется двусторонней. Поверхность, на которой не существует непрерывного вектора нормалей, называется односторонней.
Двусторонняя поверхность Ф характеризуется следующем свойством: для любой точки M  и для любого замкнутого контура, проходящего по поверхности Фи не пересекающегося с границей поверхности , выбранное в точке М направление нормали, непрерывно меняясь при движении точки по контуру, не изменит своего направления(на противоположное) при возвращении в точку М.
и для любого замкнутого контура, проходящего по поверхности Фи не пересекающегося с границей поверхности , выбранное в точке М направление нормали, непрерывно меняясь при движении точки по контуру, не изменит своего направления(на противоположное) при возвращении в точку М.
На односторонней поверхности существует такой контур, при обходе которого направление нормали изменится на противоположное.
На каждой двусторонней поверхности можно два непрерывных поля нормалей, противоположных по направлению: N(M) и –N(M). Выбор одного из этих полей называется выбором стороны поверхности. Т.О. двусторонняя поверхность имеет две стороны. Двусторонние поверхности называются также ориентируемыми, а выбор определенной стороны (выбор одного из полей) называется ориентацией поверхности. НАПРИМЕР: плоскость, сфера, гиперболоиды-двусторонние поверхности, лист Мёбиуса-односторонняя поверхность.
1.4 Пусть Ф- гладкая и кусочно гладкая ограниченная поверхность. Выберем одну из ее сторон, определяемую полем нормалей N(M). Пусть  составляет с осями координат, и пусть на поверхности Ф заданы три функции P(M),Q(M),R(M).
составляет с осями координат, и пусть на поверхности Ф заданы три функции P(M),Q(M),R(M).
Поверхностные интегралы первого рода
 ,
,
 ,
,
 , называют поверхностным интегралом второго рода соответственно от функций P,Q,R по выбранной стороне поверхности Ф. Они обозначаются:
, называют поверхностным интегралом второго рода соответственно от функций P,Q,R по выбранной стороне поверхности Ф. Они обозначаются:



2.1Запишите формулу площади поверхности, заданной уравнением
z = h (x,y), (x,y)  D , и сформулируйте условия ее применимости.
D , и сформулируйте условия ее применимости.

Если область G ограничена и замкнута, ее границей является кусочно гладкая кривая без самопересечений, функция f(x,y) непрерывно дифференцируема в области G
2.2 Гладкая параметрически заданная поверхность, не имеющая особых точек, квадрируема, и ее площадь S выражается формулой  , где
, где
 ,
,  ,
, 
 (u,v)
(u,v) 
E,G,F определяются 
Справедливо: 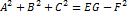
Формулу можно записать в виде  dudv
dudv
2.3 Поверхность Ф является графиком непрерывно дифференцируемой функции z=z(x,y),(x,y) 

2.4 Пусть Ф-гладкая поверхность,не имеющая особых точек,заданная параметрически уравнением  (u,v)
(u,v)  , и пусть f(x,y,z) непрерывна на Ф,тогда
, и пусть f(x,y,z) непрерывна на Ф,тогда 
E,G,F определяются 
2.5  , S задана в виде z=z(x,y) (x,y)
, S задана в виде z=z(x,y) (x,y) 

(Такие обозначение связаны с тем,что элемент площади dydz можно рассматривать как площадь проекции элемента поверхности с площадью dS на координатную плоскость Oyz, т.е dxdy= 
2.6 Поверхностный интеграл второго рода  , по выбранной стороне поверхности Ф является интегралом первого рода соответственно от функции,
, по выбранной стороне поверхности Ф является интегралом первого рода соответственно от функции, 
Пусть гладкая двусторонняя поверхность Ф задана параметрически уравнением
 (u,v)
(u,v)  и не имеет особых точе.Выберем ту сторону поверхности,на которой N(M) =
и не имеет особых точе.Выберем ту сторону поверхности,на которой N(M) =  .Тогда находим
.Тогда находим 
И получаем
 .
.
2.7 Запишем общий поверхностный интеграл второго рода:

В виде: 
Направляющие косинусы  ,
,  являются координатами единичного вектора нормали n(M) к поверхности Ф в точке М.
являются координатами единичного вектора нормали n(M) к поверхности Ф в точке М.
Такие обозначение связаны с тем,что элемент площади dydz можно рассматривать как площадь проекции элемента поверхности с площадью dS на координатную плоскость Oyz, т.е dxdy=  , dydz=dScos
, dydz=dScos 
Тема 9. Криволинейные интегралы.
1.1. Длиной кривой L называется предел длин ломаных, вписанных в кривую при  (кривая задается параметрически уравнениями
(кривая задается параметрически уравнениями 
1.2. Число I называется криволинейным интегралом 1 рода от ф-ии f(x,y) по кривой L, если существует предел  и обозначается
и обозначается  . (где
. (где  .
.
1.3. Число I1 называется криволинейным интегралом 2 рода, если  предел
предел  и обозначается следующим образом:
и обозначается следующим образом:  (где
(где  - интенральная сумма).
- интенральная сумма).
1.4. Число I2 называется криволинейным интегралом 2 рода, если  предел
предел  и обозначается следующим образом:
и обозначается следующим образом:  (где
(где  - интенральная сумма).
- интенральная сумма).
2.1.
2.2. Вычисление криволинейного интеграла  с помощью определенного.
с помощью определенного.
Если L – кусочно гладкая кривая, заданная уравнениями  и ф-я f(x,y) кусочно непрерывна вдоль кривой L, то существует криволинейный интеграл
и ф-я f(x,y) кусочно непрерывна вдоль кривой L, то существует криволинейный интеграл  и справедливо равенство:
и справедливо равенство:  .
.
[Если L задана уравнениями y=y(x),  y(x) имеет непрерывную производную на [a,b]:
y(x) имеет непрерывную производную на [a,b]:  ]; [Если кривая L задана в полярных координатах уравнением r=r
]; [Если кривая L задана в полярных координатах уравнением r=r  имеет непрерывную производную на [
имеет непрерывную производную на [  ]:
]:  ]; [для гладкой пространственной кривой, заданной параметрически уравнениями
]; [для гладкой пространственной кривой, заданной параметрически уравнениями  :
:  ]
]
2.3. Вычисление криволинейного интеграла  с помощью определенного
с помощью определенного
Если АВ – кусочно гладкая кривая, заданная уравнениями  , а ф-я Р=Р(х,у) кусочно непрерывна вдоль кривой АВ, то существует интеграл
, а ф-я Р=Р(х,у) кусочно непрерывна вдоль кривой АВ, то существует интеграл  и справедливо равенство:
и справедливо равенство:  .
.
2.4. Вычисление криволинейного интеграла  с помощью определенного
с помощью определенного
Если АВ – кусочно гладкая кривая, заданная уравнениями  , а ф-я Q=Q(х,у) кусочно непрерывна вдоль кривой АВ, то существует интеграл
, а ф-я Q=Q(х,у) кусочно непрерывна вдоль кривой АВ, то существует интеграл  и справедливо равенство:
и справедливо равенство:  .
.
2.5.
2.6. Связь криволинейного интеграла первого и второго рода.
Пусть АВ – кусочно гладкая кривая, заданная уравнениями  , ф-ии Р=Р(х,у) и Q=Q(х,у) кусочно непрерывны вдоль кривой АВ и
, ф-ии Р=Р(х,у) и Q=Q(х,у) кусочно непрерывны вдоль кривой АВ и  - единичный касательный вектор к кривой АВ в т. М(х,у), причем направление
- единичный касательный вектор к кривой АВ в т. М(х,у), причем направление  соответствует направлению движения от А к В (
соответствует направлению движения от А к В (  - угол между вектором
- угол между вектором  в т. М(х,у) и осью Ох). Тогда имеет место равенство:
в т. М(х,у) и осью Ох). Тогда имеет место равенство:  , где а=Р(х,у)i+Q(x,y)j.
, где а=Р(х,у)i+Q(x,y)j.
2.7. Теорема о формуле Грина.
Пусть ф-ии P(x,y), Q(x,y) и их частные производные  непрерывны в простой области G. Тогда справедливо равенство:
непрерывны в простой области G. Тогда справедливо равенство:  где криволинейный интеграл берется по границе L области G в положительном направлении.
где криволинейный интеграл берется по границе L области G в положительном направлении.
2.8. Условия независимости интеграла второго рода от пути интегрирования.