Главная | Обратная связь

ЗАДАЧА О НАЗНАЧЕНИЯХ. ВЕНГЕРСКИЙ МЕТОД

2.3.1. Постановка задачи.

В общем виде задача о назначениях формулируется следующим образом. Имеется m работ и n кандидатов для их исполнения. Затраты i-ого кандидата на выполнение j-ой работы равны . Каждый кандидат может быть назначен только на одну работу, и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы, при котором суммарные затраты на выполнение работ были минимальными.

Это частный случай транспортной задачи. Здесь работы – «пункты отправления», кандидаты – «пункты назначения». Предложение в каждом «пункте отправления» равно 1, т.е. для всех i. Аналогично, спрос в каждом «пункте потребления» равен 1, т.е. для всех j.

Задача о назначениях может быть задана как в стандартной (закрытой) форме так и в открытой.

При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ: n = m.

Задача о назначениях в открытой форме возникает тогда, когда количество рабочих не равно количеству работ: .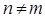

Для решения задачи о назначениях составляют таблицу, в левой колонке которой записаны номера кандидатов, в верхней строке – номера работ. Таким образом, матрица стоимостей C имеет следующий вид: в i- й строке j-го столбца стоят затраты на выполнение i-м кандидатом j-ой работы равны .

работы кандидаты			j		n
	c11		c1j	…	c1n
…	…	…	…	…	…
i	ci1		cij	…	cin
…	…	…	…	…	…
m	cm1		cmj	…	cmn

 

Прежде чем решать задачу о назначениях в открытой форме необходимо устранить дисбаланс, добавив фиктивные работы или фиктивных кандидатов в зависимости от начальных условий.

Сначала рассмотрим задачу о назначениях, полагая, что n = m.

Пусть – переменная, значение которой равно 1, если i-й кандидат выполняет j-ю работу, и 0 – в противном случае. Таким образом, решение задачи может быть записано в виде матрицы

, где -булева переменная

Допустимое решение называется назначением. Допустимое решение строится путем выбора ровно одного элемента в каждой строке матрицы и ровно одного элемента в каждом столбце этой матрицы. Для заданного значения n существует n! допустимых решений.

Тогда условие о том, что каждый кандидат может быть назначен только на одну работу, запишется в виде

Условие о том, что каждая работа может быть выполнена только одним кандидатом, запишется в виде

.

Необходимо выбрать претендентов так, чтобы суммарные затраты были минимальными, поэтому целевая функция задачи имеет вид:

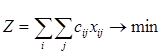
В функцию входят только те значения , для которых 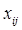отличны от 0, т.е. входят затраты, соответствующие назначенным работам.

Таким образом, экономико-математическая модель задачи может быть записана в виде:

Специфическая структура задачи позволяет применять более эффективные методом решения – Венгерским методом.

2.3.2. Венгерский метод решения задачи о назначениях

В Венгерском методе используется следующий принцип: оптимальность решения задачи не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же постоянную величину.

На основании этой теоремы можно построить новую матрицу с нулевыми элементами , и если эти нулевые элементы (или их подмножества) будут соответствовать допустимому решению, то такое решение

будет оптимальным, так как стоимость не может быть отрицательной.

Таким образом, модифицированная матрица стоимостей – это матрица, из всех элементов строк и столбцов которой нельзя вычесть никакие элементы, не получив отрицательных.

Алгоритм метода содержит следующие шаги.

Шаг 1. Получение нулей в каждой строке. Для этого в каждой строке матрицы С определяем наименьший элемент и его значение вычитаем из всех элементов этой строки.

Шаг 2. Получение нулей в каждом столбце. Для этого в каждом столбце матрицы С определяем наименьший элемент и его значение вычитаем из всех элементов этого столбца.

Шаг 3. Поиск оптимального решения. Просматривают строку, содержащую наименьшее число нулей. Отмечают один из нулей этой строки и зачеркивают все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные операции последовательно проводят для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (число отмеченных нулей равно n), то решение является оптимальным, в противном переходим к шагу 4.

Шаг 4. Поиск минимального набора строк и столбцов, содержащих все нули. Для этого необходимо отметить:

1. все строки, в которых не имеется ни одного нуля;

2. все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных строк;

3. все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов.

Действия 2) и 3) повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец.

Цель этого шага – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули.

Шаг 5. Перестановка некоторых нулей. Взять наименьшее число из тех клеток, через которые не проведены прямые. Вычесть его из каждого числа, стоящего в не вычеркнутых столбцах и прибавить к каждому числу, стоящему в вычеркнутых строках, после чего весь цикл расчета повторить начиная с шага 3.

Покажем работу венгерского алгоритма на следующем примере.

Пример. Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результаты второго проекта – это входными данными для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для реализации проекта. Матрица времен имеет вид

, где 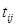время на выполнение i-м ученым j-го проекта.

Продолжительность времени задана в месяцах. Требуется выбрать научного руководителя каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным.

Решение. Данная задача является задачей о назначениях. В качестве работ рассматриваются исследовательские проекты, в качестве кандидатов – ученые, претендующие на роль руководителей.

Введем переменные

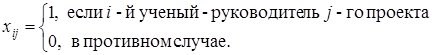
Таким образом, решение задачи может быть записано в виде матрицы .

Целевая функция задачи имеет вид

Решим задачу Венгерским методом, используя приведенную матрицу.

Выберем в каждой строке матрицы минимальный элемент и его значение вычитаем из всех элементов этой строки

Найдем в каждом столбце матрицы минимальный элемент и его значение вычитаем из всех элементов этого столбца

Строками, содержащими наименьшее число нулей (один нуль), является первая, третья и четвертая строки. Подчеркнем 0 первой строки, при этом вычеркнем 0 из первого столбца. Это вычеркивание означает, что так как первый ученый назначен научным руководителем первого проекта, второй ученый уже не может быть назначен. Отметим 0 в третьей строке и вычеркнем 0, стоящий в четвертой строке в третьем столбце, что соответствует тому, что четвертый ученый не может быть назначен научным руководителем третьего проекта. Отметим любой из нулей второй строки (действуя по порядку, отмечаем нуль, стоящий во втором столбце) и вычеркиваем 0, стоящий в четвертом столбце. Это вычеркивание означает, что так как второй ученый назначен научным руководителем второго проекта, второй ученый уже не может быть назначен руководителем четвертого проекта.

Число отмеченных нулей равно 3, т.е. назначение не является полным.

Перейдем к шагу 4.

Найдем минимальный набор строк и столбцов, содержащий все нули. Отметим точкой четвертую строку, не содержащую ни одного отмеченного нуля. Отметим точкой третий столбец, содержащий перечеркнутый нуль в четвертой строке. Отметим третью строку, содержащую отмеченный нуль в третьем столбце. Кроме третьего столбца больше нет столбцов, содержащих перечеркнутые нули в отмеченных строках. Вычеркнем отмеченный столбец и неотмеченные строки.

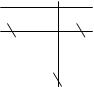
В оставшихся клетках минимальный элемент равен 2. Вычтем его из каждого числа не вычеркнутых столбцов

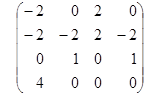
Теперь прибавим 2 к каждому числу вычеркнутых строк в преобразованной матрице и вновь сделаем назначение

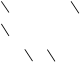
Это назначение является полным, т.к. число отмеченных нулей равно 4. Получено следующее назначение:

· первый ученый назначен научным руководителем первого проекта: ;

· второй ученый назначен научным руководителем второго проекта: ;

· третий ученый назначен научным руководителем третьего проекта: ;

· четвертый ученый назначен научным руководителем четвертого проекта: .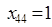

Суммарное время выполнения всех проектов равно: месяцев.

Данное назначение не единственное. Если во второй строке сначала отметить четвертый, а не второй нуль, получим следующее назначение

· первый ученый назначен научным руководителем первого проекта: ;

· второй ученый назначен научным руководителем четвертого проекта: ;

· третий ученый назначен научным руководителем третьего проекта: ;

· четвертый ученый назначен научным руководителем второго проекта: .

Суммарное время выполнения всех проектов не изменилось: .

2.3.3. Решение задачи о назначениях при помощи преобразования матрицы стоимостей

Рассмотрим решение задачи о назначениях, в которой нужно найти максимум функции Z.

Пример. В конкурсе на занятие пяти вакансий участвуют семь претендентов. Результаты тестирования каждого претендента, на соответствующие вакансии, даны в виде матрицы стоимостей – С (тестирование проводилось по десятибалльной системе):

.

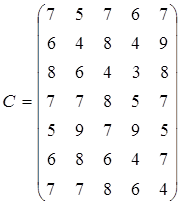Определить, какого претендента и на какую вакансию следует принимать, причем так, чтобы сумма баллов отобранных претендентов оказалась максимальной.

Экономико-математическая модель задачи может быть записана в виде:

В этой задаче присутствует дисбаланс, поэтому предварительно ее нужно сбалансировать. Эта процедура выполняется добавлением двух столбцов (две фиктивные вакансии) с нулевыми результатами тестирования:

Задача нахождения максимального значения функции Z эквивалентна задаче нахождения минимума длz функции .

Матрица (–С)имеет вид:

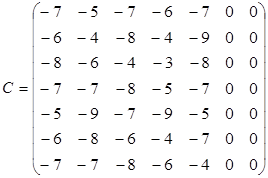
В каждой строке и в каждом столбце матрицы (–С) необходимо получить нули, вычитая минимальные элементы из соответствующих строк или столбцов. В рассматриваемом примере в каждой строке матрицы С нули есть (они появились о результате добавления фиктивных вакансий). Чтобы образовать нули в первых пяти столбцах матрицы, определим минимальные элементы в этих столбцах и вычтем их из соответствующих столбцов матрицы. В результате получим следующую матрицу:

Строками, содержащими наименьшее число нулей (два нуля), является первая и шестая строки. Подчеркнем 0 первой строки, при этом вычеркнем все нули, стоящие в первой строке и шестом столбце. Отметим 0 в шестой строке и при этом вычеркнем все нули, стоящие в седьмом столбце. Отметим 0 в третьей строке. Затем отметим 0 в четвертой строке и вычеркнем все нули, стоящие в третьем столбце. Отметим 0 во второй строке. Отмечая один из нулей в пятой строке, вычеркнем нуль второй 0, стоящий в этой строке в четвертом столбце. Это означает, что третий претендент не может быть назначен на две вакансии одновременно.

Таким образом, число отмеченных нулей равно 6, т.е. назначение не является полным.

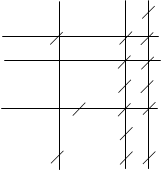Найдем минимальный набор строк и столбцов, содержащий все нули. Отметим точкой седьмую строку, не содержащую ни одного отмеченного нуля. Отметим точками третий, шестой и седьмой столбцы, содержащие перечеркнутые нули. Отметим первую, четвертую и шестую строки, содержащие отмеченные нули в третьем, шестом и седьмом столбцах. Больше нет столбцов, содержащих перечеркнутые нули в отмеченных строках. Вычеркнем отмеченные столбцы и неотмеченные строки.

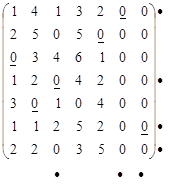
В оставшихся клетках минимальный элемент равен 1. Вычтем его из каждого числа не вычеркнутых столбцов

Теперь прибавим 1 к каждому числу вычеркнутых строк (второй, третьей, пятой) в преобразованной матрице и вновь сделаем назначение

Это назначение является полным, т.к. число отмеченных нулей равно 7. Перенеся полученное решение на исходную матрицу С получим, что первый и седьмой претенденты попадают на фиктивные вакансии и не принимаются на работу, второй претендент принимается на пятую вакансию, третий – на первую, четвертый – на третью, пятый– на четвертую и шестой– на вторую.

Сумма баллов, полученная при данном решении равна:

.

 

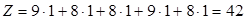2.2.4. Решение задачи о назначениях средствами Excel

Решим задачу о назначениях, рассмотренную в предыдущем примере средствами Excel. Исходные условия этой задачи представлены в таблице листа Excel на рис. 1.

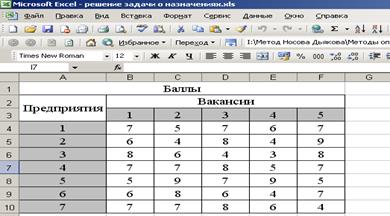
Рис. 1

1. Ввод данных. Вводим данные задачи в Excel, при этом нужно ввести два столбца (6-ой и 7-й) с нулевыми значениями для сбалансирования задачи. Результаты заполнения таблицы Excel можно увидеть на рис. 2.

В ячейках В4:F10 введены результаты тестирования претендентов, а в ячейках G4:Н10 введены нули, что соответствует фиктивным вакансиям.

Ячейки В14:Н20 находятся изменяемыми ячейками для процедуры «Поиск решения...».

В ячейках В21:Н21 находятся суммы значений соответствующих столбцов изменяемых ячеек. Так, в ячейке В21 находится сумма ячеек В14:В20. Аналогично в ячейках:

в С21 находится сумма ячеек С14:С20;

в D21 находится сумма ячеек D14: D20;

в Е21 находится сумма ячеек Е14:Е20;

в F21 находится сумма ячеек F14: F20.

в G21 находится сумма ячеек G14: G20;

в Н21 находится сумма ячеек Н14:Н20.

В ячейках I14:I20 находятся суммы значений соответствующих строк изменяемых ячеек. Так, в ячейке I14 находится сумма ячеек В14:Н14. Аналогично в ячейках:

в I15 находится сумма ячеек В15:Н15;

в I16 находится сумма ячеек В16:Н16;

в I17 находится сумма ячеек В17:Н17;

в I18 находится сумма ячеек В18:Н18;

в I19 находится сумма ячеек В19:Н19;

в I20 находится сумма ячеек В20:Н20.

Целевая функция заносится в ячейку J3 и вычисляется по формуле «СУММПРОИЗВ(В4:Н10;В14:Н20)».

Рис. 2

2. Заполнение окна процедуры «Поиск решения…».

Целевая функция: J3.

Значение целевой функции: mах.

Изменяемые ячейки: В14:Н20.

Ограничения задачи:

В21:Н21=1 и 114:120 =1 (все свободные рабочие места должны быть заняты и все претенденты размещены по вакансиям);

В14:Н20 (изменяемые ячейки должны иметь положительные значения);

В14:Н20 — двоичные числа.

В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом. Результаты заполнения окна показаны на рис. 3.

Рис. 3

 

3. Выполнив процедуру «Поиск решения...», мы получили в первоначальной таблице следующие результаты (рис. 4).

Рис. 4

Эти результаты совпадают с решением задачи, полученным преобразованием матрицы (С).

В ячейках, обведенных жирной рамкой, получено оптимальное решение задачи о назначениях, а именно:

.

В ячейке J3 находится максимальное значение целевой функции: Z_min=42.

2.3.5. Применение задачи о назначениях к решению экономических задач