Лінійні дії над векторами

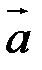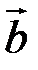Нехай задано два вектори і . Оскільки вектори можна переносити

до будь якої точки простору, то, не обмежуючи загальності, можна вважати, що початок вектора 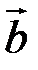збігається з кінцем вектора .

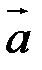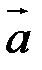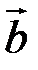Означення. Сумою векторів і називається вектор , початок якого збігається з початком вектора 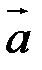, а кінець – з кінцем вектора 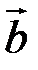(рис. 4).

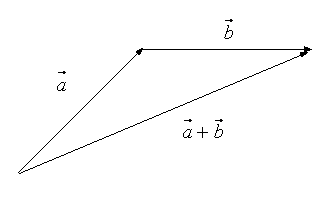
Рис. 4

Таке правило додавання векторів називається правилом трикутника (з рисунка 4 видно чому). В деяких задачах доцільно користуватися іншим правилом. Припустимо, що вектори 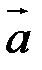і 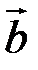збігаються своїми початками. Побудуємо на цих векторах паралелограм так, що 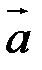і 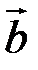є його суміжними сторонами. Діагональ цього паралелограма, що йде від точки прикладання векторів 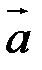і 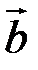до протилежної вершини паралелограма, й є сума векторів 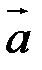і 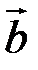(рис. 5).

Рис. 5

Легко переконатися в еквівалентності правила трикутника і правила паралелограма. Саме за правилом паралелограма знаходиться рівнодіюча двох сил та .

Правило додавання двох векторів легко узагальнити на будь яке число векторів (рис. 6).

Рис. 6

Розглянемо питання про віднімання векторів. Нехай вектори і збігаються своїми початками.

Означення. Різницею векторів і називається вектор , початок якого збігається з кінцем вектора , а кінець – з кінцем вектора (рис. 7).

Рис. 7

Легко переконатися (за правилом трикутника), що , і таким чином саме таке правило віднімання векторів є природним.

Означення. Добутком вектора на число називається вектор , довжина якого дорівнює , а напрям збігається за напрямом вектора , якщо , і протилежний йому, якщо . Якщо 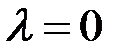, або , то .

Теорема. Вектори і колінеарні тоді і тільки тоді, коли існує таке число , що .

Доведення. Будемо вважати, що вектори і ненульові (у протилежному випадку , і нульовий вектор колінеарний будь якому вектору).

Необхідність. Нехай вектори і колінеарні. Для визначеності припустимо, що вони збігаються напрямами. Розглянемо одиничний вектор , напрям якого також збігається з напрямами векторів і (рис. 8).