Главная | Обратная связь

Скалярний добуток векторів.

 

Означення.Скалярним добутком векторів і називається добуток довжин цих векторів на косинус кута між ними (рис. 23).

 

 

Рис. 23

.

Оскільки , то

.

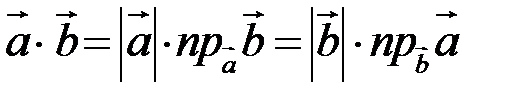Поняття скалярного добутку векторів широко використовується у математиці та суміжних науках. Розглянемо, наприклад, силу 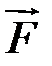, що діє на матеріальне тіло під кутом до напряму переміщення цього тіла (рис. 24).

 

 

Рис. 24

 

Тоді робота цієї сили 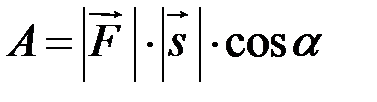, тобто . Зокрема, якщо напрям дії сили збігається з напрямом переміщення, тобто , , то .

Визначимо деякі важливі властивості скалярного добутку.

1. .

Дійсно: .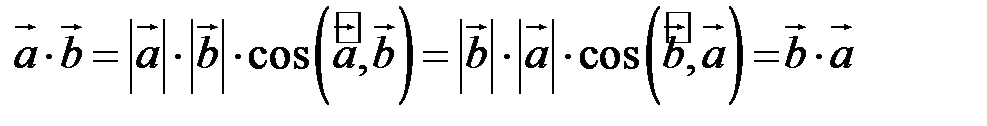

Тобто скалярний добуток має властивість комутативності.

2. .

Дійсно .

3. .

Дійсно

.

4. Скалярний добуток двох ненульових векторів дорівнює нулю тоді і

тільки тоді, коли ці вектори перпендикулярні.

Справді, якщо 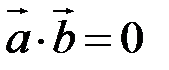, тобто при тому, що , , то 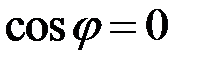, тобто .

5.

Тобто скалярний квадрат вектора дорівнює квадрату його довжини. Звідси зокрема маємо:

.

Приклад. Знайти скалярний добуток векторів 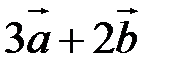і , якщо , , .

Маємо: ; , ; .

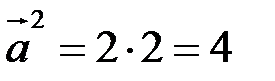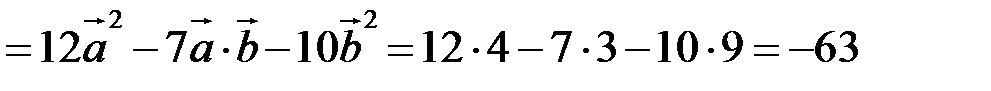Нехай ­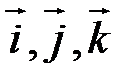 – вектори ортонормованого базису. Розглянемо:

,

.

Припустимо тепер, що вектори задано своїми координатами:

.

Знайдемо (на підставі властивостей 1–3 скалярного добутку):

.

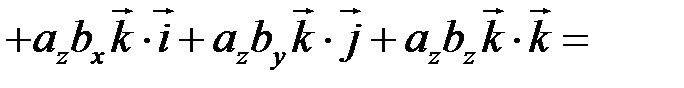
Отже отримали вираз скалярного добутку векторів і через їх координати:

.

Тобто скалярний добуток двох векторів дорівнює сумі добутків їх відповідних координат.

Зокрема для скалярного квадрата вектора маємо:

.

Таким чином ми отримуємо формулу для довжини вектора :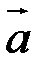

.

Кут 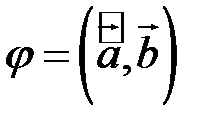між векторами і визначиться формулою:

.

Приклад. Трикутника задано його вершинами , . Знайти його внутрішній кут при вершині .

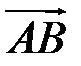Очевидно, що кут це кут між векторами та (рис. 25).

 

 

Рис. 25

 

 

Маємо:

.

Звідси .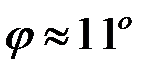

Оскільки , то з формули кута між векторами випливає славнозвісна нерівність Коші–Буняковського:

.

Або у координатній формі:

.