 |
|
Поверхні та лінії у просторі
Розглянемо деяку поверхню 
у тривимірному просторі (рис. 30).
Рис. 30
Відмітимо, що строго визначити поняття поверхні неможливо, і ми змушені розуміти його на інтуїтивному рівні (також, як і поняття точки, лінії). Наприклад, поверхня Землі, поверхня мильної кулі, тощо. Геометричну модель поверхні можна отримати, якщо взяти аркуш паперу і певним чином зігнути його.
Нехай 
– довільна точка поверхні .
Означення.Рівняння вигляду
,
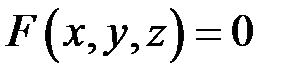яке задовольняють координати будь якої точки на поверхні, і не задовольняють координати ніякої іншої точки простору, називається рівнянням поверхні.
Для отримання такого рівняння для деяких поверхонь можна використати їх означення як геометричного місця точок.
Приклад. Знайдемо рівняння сфери, виходячи з її означення, як геометричного місця точок, рівновіддалених від однієї заданої точки (центра сфери). Моделлю сфери, близькою до ідеальної, є мильна кулька.
Нехай центром сфери є точка 
, і 
– радіус сфери. Нехай 
– довільна точка сфери. Тоді 
. Згідно з формулою відстані між двома точками (див. п.6):
,
Звідси:
.
Це й є шукане рівняння сфери. Зокрема, якщо центром сфери є початок координат 
, то рівняння набуває вигляду:
.
Якщо вираз 
в рівнянні поверхні є многочленом від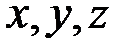 
, тобто сумою скінченного числа одночленів 
зі сталими коефіцієнтами 
і натуральними показниками 
, то поверхня називається алгебраїчною. Наприклад, сфера – це алгебраїчна поверхня. Порядком алгебраїчної поверхні називається степінь многочлена, яким задається рівняння цієї поверхні. Сфера – алгебраїчна поверхня 2-го порядку. Неалгебраїчні поверхні називаються трансцендентними. Ми розглядатиме лише алгебраїчні поверхні 1-го та 2-го порядків.
Розглянемо тепер питання про опис лінії у просторі. Тут є такі можливості. Лінію можна задати як перетин двох поверхонь (рис. 31).
Рис. 31
Якщо поверхні задано своїми рівняннями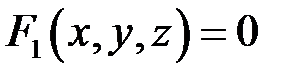 
та 
, то координати будь якої точки на лінії мають задовольняти систему двох рівнянь з трьома невідомими:
Такі рівняння і називаються рівняннями лінії у просторі.
Інша можливість – параметричні рівняння лінії. Вони виникають таким чином. Розглянемо (рис. 32) вектор 
з початком у точці 
, довжина і напрям якого змінюються з часом 
(тобто у кожний момент часу вектор 
має свою довжину і напрям). Тоді з перебігом часу кінець цього вектора буде описувати лінію, яка називається годографом вектора . А рівняння
називається векторним параметричним рівнянням цієї лінії. Якщо це рівняння переписати у координатній формі:
,
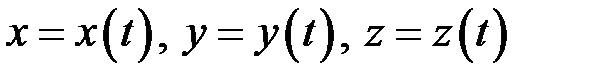то отримаємо скалярні параметричні рівняння лінії у просторі. У подальшому ми отримаємо рівняння деяких конкретних ліній.
Рис. 32