 |
|
Поверхні другого порядку
Як ми вже відмічали, площина являється поверхнею першого порядку, її рівняння лінійне відносно  . Якщо поверхня описується рівнянням 2-го порядку відносно
. Якщо поверхня описується рівнянням 2-го порядку відносно  , тобто рівнянням вигляду:
, тобто рівнянням вигляду:
 ,
,
то така поверхня називається поверхнею 2-го порядку. При цьому припускається, що принаймні один з коефіцієнтів  відмінний від нуля (у протилежному випадку ми отримуємо поверхню 1-го порядку, тобто площину).
відмінний від нуля (у протилежному випадку ми отримуємо поверхню 1-го порядку, тобто площину).
Розглянемо деякі важливі типи поверхонь 2-го порядку.
1. Циліндричні поверхні. Циліндричною називають поверхню, утворену множиною прямих (твірних), які перетинають задану лінію  (напрямну) і паралельні заданій прямій
(напрямну) і паралельні заданій прямій  .
.
Ми обмежимось випадком, коли напрямні лежать в одній з координатних площин, а твірні паралельні координатній осі, перпендикулярній цій площині. Наприклад, напрямна лежить в площині  , а твірні паралельні осі
, а твірні паралельні осі  (рис. 42).
(рис. 42).
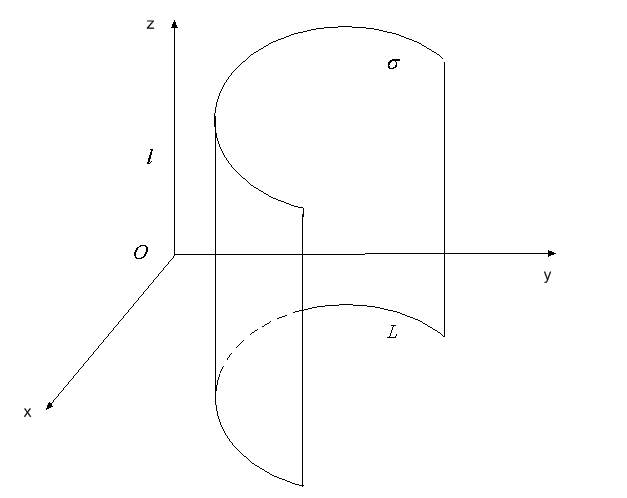
Рис. 42
Якщо в площині  лінія
лінія  описується рівнянням
описується рівнянням
 ,
,
то саме таке рівняння буде описувати у просторі  циліндричну поверхню
циліндричну поверхню  , напрямною якої є лінія
, напрямною якої є лінія  , а твірні паралельні осі
, а твірні паралельні осі  . Дійсно, якщо
. Дійсно, якщо  – точка цієї поверхні, то координати
– точка цієї поверхні, то координати  будуть збігатися з координатами точки на лінії
будуть збігатися з координатами точки на лінії  , а координата
, а координата  буде довільною.
буде довільною.
Приклади. 1). Круговий циліндр. Це поверхня, що визначається рівнянням:
 .
.
Її напрямною є коло  на площині
на площині  (рис. 43).
(рис. 43).

Рис. 43
2). Еліптичний циліндр.
 .
.
Напрямною є еліпс  (рис. 44).
(рис. 44).

Рис. 44
3). Параболічний циліндр.
 .
.
Напрямною є парабола 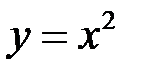 (рис. 44).
(рис. 44).

Рис. 44
2. Конічні поверхні. Конічною називається поверхня, яку утворено множиною прямих, що проходять через задану точку  і перетинають задану лінію
і перетинають задану лінію  (рис. 45). При цьому
(рис. 45). При цьому 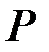 називається вершиною поверхні, лінія
називається вершиною поверхні, лінія  – напрямною, а кожна з прямих, що утворюють поверхню – твірною.
– напрямною, а кожна з прямих, що утворюють поверхню – твірною.

Рис. 45
Приклади. 1). Еліптичний конус.
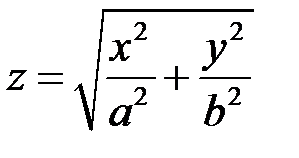 .
.
Вершиною є точка  , а напрямною еліпс
, а напрямною еліпс

в площині  (рис. 46).
(рис. 46).

Рис. 46
Якщо, зокрема 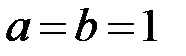 , то маємо круговий конус
, то маємо круговий конус  , напрямною якого є коло
, напрямною якого є коло  у площині
у площині  . Цей конус можна отримати обертанням графіка функції
. Цей конус можна отримати обертанням графіка функції  навколо осі ординат.
навколо осі ординат.
3. Еліптичний параболоїд. Еліптичним параболоїдом називається поверхня, яка описується рівнянням:
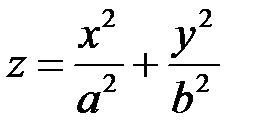 .
.
Перерізи цієї поверхні будь якою площиною  є еліпсами:
є еліпсами:
 .
.
Зокрема, якщо 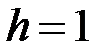 , то отримуємо еліпс з півосями
, то отримуємо еліпс з півосями  і
і 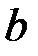 . Перерізи поверхні площинами
. Перерізи поверхні площинами  та
та  є параболами відповідно
є параболами відповідно  та
та  (рис. 47).
(рис. 47).
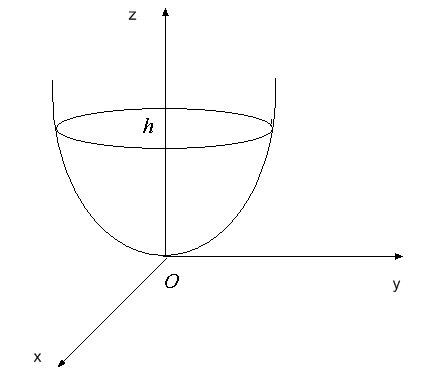
Рис. 47
Якщо, зокрема 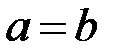 , то отримуємо параболоїд обертання:
, то отримуємо параболоїд обертання:
 .
.
Його можна отримати обертанням параболи  навколо осі ординат.
навколо осі ординат.
4. Однопорожнинний гіперболоїд. Однопорожнинним гіперболоїдом називається поверхня, що описується рівнянням:
 .
.
Розглянемо перерізи цієї поверхні площинами  :
:
 .
.
Позначаючи  , отримаємо:
, отримаємо:
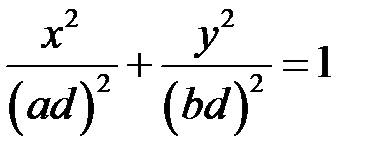 ,
,
тобто еліпси з півосями  і
і  . Зокрема при
. Зокрема при  (тоді
(тоді  ) півосі дорівнюють
) півосі дорівнюють  і
і  (горловий еліпс). Таким чином горизонтальні перерізи нашої поверхні площинами
(горловий еліпс). Таким чином горизонтальні перерізи нашої поверхні площинами  є еліпсами. Півосі цих еліпсів збільшуються зі зростанням
є еліпсами. Півосі цих еліпсів збільшуються зі зростанням  .
.
Розглянемо тепер перерізи поверхні площинами  :
:
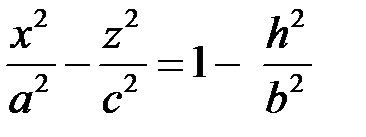 .
.
Позначаючи 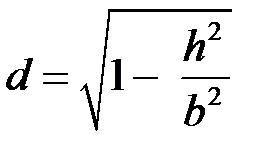 , отримаємо:
, отримаємо:
 ,
,
тобто гіперболи з півосями  ,
,  . Зокрема при
. Зокрема при  (тобто площина
(тобто площина  ) буде
) буде  , і маємо:
, і маємо:
 ,
,
тобто гіпербола з півосями  . Аналогічно перерізи поверхні площинами
. Аналогічно перерізи поверхні площинами  також уявляють собою гіперболи. Поверхня має вигляд, який показано на рис. 48.
також уявляють собою гіперболи. Поверхня має вигляд, який показано на рис. 48.

Рис. 48
Однопорожнинний гіперболоїд має цікаву властивість: наявність прямих, які цілком лежать на цій поверхні (прямолінійні твірні). Через кожну точку гіперболоїда проходить дві прямі, рівняння яких можна отримати наступним чином. Запишемо рівняння поверхні так:
 .
.
Розкладемо обидві частини на множники:
 . (*)
. (*)
Тепер розглянемо пряму лінію, яку задано рівняннями:
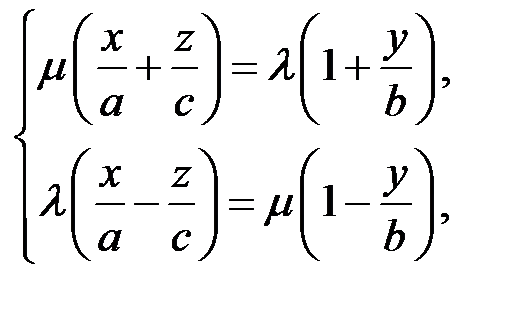 (**)
(**)
де  – деякі числа. Координати кожної точки прямої задовольняють обидва рівняння, отже їх добуток, тобто рівняння (*). Тому всі точки прямої лінії з рівняннями (**) лежать на однопорожнинному гіперболоїді. Такі ж міркування можна провести і для сім’ї прямих:
– деякі числа. Координати кожної точки прямої задовольняють обидва рівняння, отже їх добуток, тобто рівняння (*). Тому всі точки прямої лінії з рівняннями (**) лежать на однопорожнинному гіперболоїді. Такі ж міркування можна провести і для сім’ї прямих: 
Всі ці прямі проходять через горловий еліпс гіперболоїда (рис. 48).
У зв’язку з цим однопорожнинний гіперболоїд називається лінійчатою поверхнею. Така його властивість використовується в архітектурі, зокрема в Шуховській вежі в Москві.
5. Двопорожнинний гіперболоїд. Двопорожнинним гіперболоїдом називається поверхня, яка визначається рівнянням:
 .
.
Розглянемо перерізи цієї поверхні площинами  . Матимемо:
. Матимемо:
 .
.
Звідси 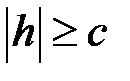 , тобто
, тобто  або
або 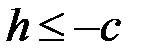 . Позначаючи
. Позначаючи  , дістаємо рівняння:
, дістаємо рівняння:
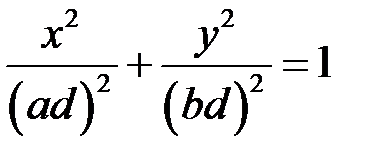 ,
,
тобто еліпс з півосями  і
і  . Перерізи поверхні площинами
. Перерізи поверхні площинами  або
або  є гіперболами (встановіть самостійно). Поверхня має вигляд, зображений на рис. 49.
є гіперболами (встановіть самостійно). Поверхня має вигляд, зображений на рис. 49.

Рис. 49
6. Гіперболічний параболоїд. Гіперболічним параболоїдом називається поверхня, яка визначається рівнянням:
 .
.
Перерізи поверхні площинами  є гіперболами, а площинами
є гіперболами, а площинами  – параболами. Поверхня має форму сідла (рис. 50).
– параболами. Поверхня має форму сідла (рис. 50).

Рис. 50
7. Сфера. Сферою називають множину всіх точок простору, рівновіддалених від заданої точки, яка називається центром сфери (рис. 51). Рівняння у ПДСК сфери з центром у точці  і радіусом
і радіусом  ми отримали в п. 11:
ми отримали в п. 11:
 .
.
Якщо, зокрема, центр сфери знаходиться у початку координат, то рівняння набуває вигляду:
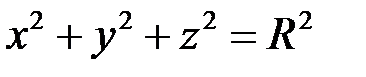
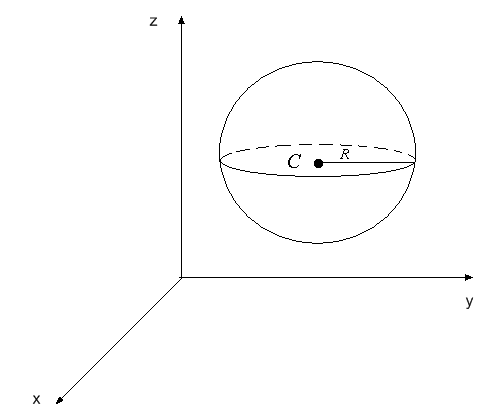
Рис. 51
Приклад. Знайти центр і радіус сфери, яку задано рівнянням:
 .
.
Виділяючи повні квадрати, запишемо рівняння у вигляді:
 ,
,
або
 .
.
Отже центром сфери є точка  , а радіус дорівнює 5.
, а радіус дорівнює 5.
8. Еліпсоїд. Еліпсоїдом називається поверхня, яка описується рівнянням:
 .
.
Розглянемо переріз поверхні площинами  :
:
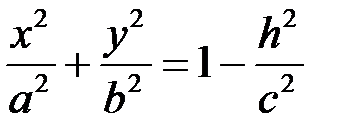 .
.
Або, позначаючи  , дістаємо:
, дістаємо:
 ,
,
тобто еліпс з півосями  і
і  . Аналогічно еліпси також будуть отримуватись у перерізах поверхні площинами
. Аналогічно еліпси також будуть отримуватись у перерізах поверхні площинами  та
та  . Поверхня має вигляд, який показано на рис. 52.
. Поверхня має вигляд, який показано на рис. 52.

Рис. 52
Числа  називаються півосями еліпсоїда. Якщо всі три півосі різні, то еліпсоїд називається триосним. Якщо будь які дві півосі рівні між собою, а третя не співпадає з ними, то еліпсоїд називається двоосним. Форма земної поверхні (геоїд) дуже близька саме до двоосного еліпсоїда. Дві півосі такого еліпсоїда дорівнюють відстані
називаються півосями еліпсоїда. Якщо всі три півосі різні, то еліпсоїд називається триосним. Якщо будь які дві півосі рівні між собою, а третя не співпадає з ними, то еліпсоїд називається двоосним. Форма земної поверхні (геоїд) дуже близька саме до двоосного еліпсоїда. Дві півосі такого еліпсоїда дорівнюють відстані  від центра Землі до екватора, а саме 6378245 м, а третя піввісь
від центра Землі до екватора, а саме 6378245 м, а третя піввісь  – відстані від центра Землі до полюсів, а саме 6356853 м (рис. 53).
– відстані від центра Землі до полюсів, а саме 6356853 м (рис. 53).

Рис. 53
Таким чином, екваторіальний радіус  Землі приблизно на 21,4 км більше, ніж її полярний радіус
Землі приблизно на 21,4 км більше, ніж її полярний радіус  . Відстань
. Відстань 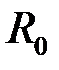 від центра Землі до точки на земній поверхні на широті
від центра Землі до точки на земній поверхні на широті  може бути знайдено за формулою:
може бути знайдено за формулою:
 .
.
Зокрема, якщо  , то
, то  , а якщо
, а якщо 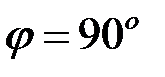 , то
, то  .
.
Якщо всі три півосі еліпсоїда співпадають, тобто  , то отримуємо сферу радіуса
, то отримуємо сферу радіуса 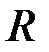 .
.
Зауваження. Якщо центр еліпсоїда знаходиться у точці 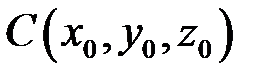 , то його рівняння має вигляд:
, то його рівняння має вигляд:
 .
.
Приклад. Довести, що поверхня, яку задано рівнянням

описує еліпсоїд, знайти його центр і півосі.
Перепишемо рівняння у вигляді:
 .
.
Або:
 .
.
Звідси видно, що це рівняння описує еліпсоїд з центром у точці  і півосями
і півосями  .
.