Главная | Обратная связь

Булевское программирование

Введение

Целочисленное программирование – один из наиболее молодых, перспективных и быстро развивающихся разделов математического программирования.

Источником задач целочисленного программирования является техническая, экономическая и военная проблематика.

 

Условие целочисленности переменных формально отражает:

а) физич. неделимость объектов (например, при размещении предприятий или выборе варианта боевых действий);

б) конечность множества допустимых вариантов, на котором проводится оптимизация (например, множества перестановок в задачах упорядочения);

в) наличие логических условий, выполнение или невыполнение которых влечет изменение вида целевой функции и ограничений задачи.

 

Можно перечислить большое количество разнообразных задач планирования экономики, организации производства, исследования конфликтных ситуаций, синтеза схем автоматического регулирования, которые формально сводятся к выбору лучших, в некотором смысле, значений параметров из определенной дискретной совокупности заданных величин. К ним можно отнести и экстремальные комбинаторные задачи, возникающие в различных разделах дискретной математики.

 

Основные понятия.

Целочисленные задачи математического программирования могут возникать различными путями.

 

1. Существуют задачи линейного программирования, которые формально к целочисленным не относятся, но при соответствующих исходных данных всегда обладают целочисленным планом. Примеры таких задач – транспортная задача и ее модификации (задачи о назначениях, о потоках в сетях).

 

2. Толчком к изучению целочисленных задач в собственном смысле слова явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины. Они были названы задачами с неделимостью. Таковы, например, задачи об оптимизации комплекса средств доставки грузов, о нахождении минимального порожнего пробега автомобилей при выполнении заданного плана перевозок, об определении оптимального машинного парка и его оптимального распределения по указанным работам при условии минимизации суммарной стоимости (машинного парка и производимых работ), о нахождении минимального количества судов для осуществления данного графика перевозок и т. п.

 

3. Другим важным толчком к построению теории целочисленного программирования стал новый подход к некоторым экстремальным комбинаторным задачам. В них требуется найти экстремум целочисленной линейной функции, заданной на конечном множестве элементов. Такие задачи принято называть задачами с альтернативными переменными. В качестве примеров можно назвать задачи коммивояжера (бродячего торговца), об оптимальном назначении, теории расписания, или календарного планирования, и задачи с дополнительными логическими условиями (например, типа «или – или», «если – то» и т. п.).

 

При рассмотрении целого ряда задач финансового менеджмента и бизнеса необходимо учитывать требование целочисленности использу­емых переменных. Такие задачи называются задачами целочисленного программирования. Целочисленным (иногда его называют также дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна.

 

 

Булевское программирование

К частному случаю задачи целочисленного линейного программирования относятся задачи, где переменные X могут принимать всего лишь два значения — 0 и 1. Соответствующие задачи часто называют задачами булевского программирования.

Наиболее известные из этих задач — задача о назначениях (какого работника на какую работу поставить), задача выбора маршрута (задача коммивояжера, задача почтальона), задача о максимальном паросочетании и т. д.

Целочисленное программирование применяется при решении задачи оптимизации развития компании, в которой 0 или 1 означают покупку какого-либо оборудования.

 

Для решения задач этого типа разрабатываются специфические алгоритмы, основанные на комбинаторике, графах и т. д.

 

Графический метод

При наличии в задаче линейного программирования двух переменных, задача может быть решена графическим методом.

В системе координат X1 X2 находят область допустимых решений, строят вектор С и линию уровня, перемещая линию уровня по направлению С для задач на максимум, определяют наиболее удаленную от начала координат точку и ее координаты.

В случае, когда координаты этой точки нецелочисленные, в области допустимых решений строят целочисленную решетку и находят на ней такие целые числа x1 и x2, которые удовлетворяют системе ограничений и при которых значение целевой функции наиболее близко к экстремальному нецелочисленному решению. Координаты такой вершины являются целочисленным решением.

Аналогично решается задача на минимум. Целочисленному минимуму целевой функции будет соответствовать координаты вершины целочисленной решетки, лежащей в области допустимых решений, наиболее близкой к началу координат в направлении вектора С.

Метод Гомори

Алгори́тм Го́мори — алгоритм, который используется для решения полностью целочисленных задач линейного программирования. Алгоритм включает в себя:

1. Решение задачи одним из методов группы симплекс-методов или группы методов внутренней точки без учёта требования целочисленности. Если полученное оптимальное решение целочисленно, то задача решена.

2. Составляется дополнительное ограничение для переменной , которая в оптимальном плане имеет максимальное дробное значение, хотя должна быть целой. Тогда величины коэффициентов элементов , вычисляются так:

где — целая часть числа . Тогда дополнительное ограничение формируется следующим образом:

Оно будет целым неотрицательным при целых неотрицательных и После составления ограничения оно вводится в систему линейных ограничений и задача решается заново при исходных ограничениях и дополнительном ограничении. Если получено целочисленное решение, задача решена. В противном случае необходимо повторить второй этап.

Для построения ограничения выбираем компоненту оптимального плана с наибольшей дробной частью и по соответствующей этой компоненте k-й строке симплексной таблицы записываем ограничение Гомори.

, ,

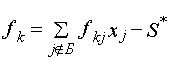где f_k = x_j - [x_j];

f_kj = z_kj - [z_kj];

S^* - новая переменная;

[x_j], [z_kj] -ближайшее целое, не превосходящее x_j и z_kj соответственно.

 

3. Составленное ограничение добавляем к имеющимся в симплексной таблице, тем самым получаем расширенную задачу. Чтобы получить опорный план этой задачи, необходимо ввести в базис тот вектор, для которого величина минимальна. И если для этого вектора величина получается по дополнительной строке, то в следующей симплексной таблице будет получен опорный план. Если же величина 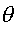не соответствует дополнительной строке, то необходимо переходить к М-задаче (вводить искусственную переменную в ограничение Гомори).

4. Решаем при помощи обычных симплексных преобразований полученную задачу. Если решение этой задачи приводит к целочисленному оптимальному плану, то искомая задача решена. Если мы получили нецелочисленное решение, то снова добавляем одно дополнительное ограничение, и процесс вычислений повторяется. Проделав конечное число итераций, либо получаем оптимальный план задачи целочисленного программирования, либо устанавливаем ее неразрешимость.

Замечания:

1. Если дополнительная переменная S^* вошла в базис, то после пересчета какого-либо последующего плана соответствующие ей строку и столбец можно удалить (тем самым сокращается размерность задачи).

2. Если для дробного x_j обнаружится целочисленность всех коэффициентов соответствующего уравнения (строки), то задача не имеет целочисленного решения.