Главная | Обратная связь

Алгебра линейной и сетевой топологии тетрарной референции

 

Основанием для осуществления усилий в направлении создания алгебры линейной и сетевой топологии тетрарной референции являются компьютерные сети, где происходит коммуникация: прием (чтение запрошенных или получение предоставленных) данных и трансляция (передача предоставляемых или диктовка запрошенных) данных.

Поскольку в сетевой топологии мы постоянно будем иметь дело с разным размещением тетрарных референций, то нужно принять к сведению следующие обстоятельства. Мы будем применять различие позиций при помощи букв для удобства опознания названий в указанной главе, но не для самой алгебры. Алгебра линейной и сетевой топологии тетрарной референции является чисто дирекциональной, в ней различие активных и пассивных позиций практически не участвует, если иное не требуется для какой-либо практической задачи.

Для понимания алгебры линейной топологии тетрарной референции мы напомним представления о референтности и референциале. Тетрарная референтность двух позиций «ак» и «па» это обозначение всех направлений — открытых референций и барьеров — при помощи тетрарной референции. Например, тетрарная референтность в выражении C D это «щит «па-от»», то есть референция с барьером. Референциал зависит от маршрута-пути. Например, референциал позиции D для маршрута-пути (C—D) будет . Референциал позиции C для маршрута-пути (D—C) будет .

Позиций может быть много, они могут быть выстроены в линию или в линейные участки сети, между ними может быть разная референтность. В таком случае мы имеем дело с маршрутом, который может быть разветвлен на разные пути. В линейной топологии, которую мы пока рассматриваем, это будет прямой и обратный пути. Как мы показали, любая сеть может быть сведена к соединению нескольких линейных участков, а значит, представление о пути является универсальным как для линейной, так и для сетевой топологии, где различены линейные ее части.

Референциал каждой позиции зависит от сумы межпозиционных референциалов всего отрезка пути линии (или сети) к данной позиции. Референциал имеет свойство передаваться в данной позиции от предыдущей позиции к следующей позиции по данному пути, если путь не заканчивается. Референциал позиции, лежащей на проходном линейном или сетевом пути называется промежуточным референциалом. Референциал позиции, оказывающейся в конце линейного или сетевого пути некоторого локуса называется концевым референциалом, референциал, находящийся в сетевом тупике (схождение всех сетевых путей^[72]) называется конечным, а референциал лежащий в начале всех сетевых путей, является начальным^[73].

Для исчисления референциалов используется референциальная алгебра. Здесь в отличие от позиционно-референциальной алгебры, мы различаем разные референциальные алгебры тетрарной референции: алгебру слияния, алгебру поглощения и алгебру разделения.

Алгебра слияния и поглощения используется в сетях, где есть закрытые барьерами локусы и открытые локусы согласно политике безопасности. Локусы, содержащие барьеры по всем маршрутам к другим участкам сети, называются закрытыми. Локусы, частично содержащие барьеры по всем маршрутам к другим участкам сети, являются частично закрытыми или частично открытыми локусами. Локусы, совсем не содержащие барьеров по всем маршрутам к другим участкам сети, являются открытыми.

Алгебра слияния референциалов пути или маршрута линии или сети позволяет референциально исчислять такую линию или сеть, где открытые потоки одного течения, выраженные тетрарным референциалом, суммируются в направлении маршрута от закрытого участка сети к открытому. Алгебра поглощения референциалов пути или маршрута линии или сети позволяет референциально исчислять такую линию или сеть, где каждый следующий тетрарный референциал поглощает предыдущий в направлении маршрута от открытого участка сети к закрытому. Алгебра разделения референциалов пути или маршрута линии или сети позволяет референциально исчислять такую линию или сеть, где каждый тетрарный референциал имеет свое собственное течение.Алгебра слияния используется для исчисления отношений между позициями в ячеистой сетевой топологии, особенно, когда один ячеистый локус соединен с другим ячеистым локусом посредством многих течений. Существуют также и другие ситуации применения этих различных алгебр.

Референциальная алгебра слияния является коммутативной и выглядит так:

Референции

Референциальная алгебра поглощения является некоммутативной, то есть в нижеследующей таблице, где производится поглощение референциалов, мы предполагаем, что первыми слагаемыми будут те, которые находятся в левом столбце, и соответственно они будут поглощающими. Референциальная алгебра поглощения выглядит так:

Референции

Референциальная алгебра разделения предполагает, что каждый референциал представляет собой отдельное четырехпотоковое течение. Таким образом, в алгебре разделения реализовывается ситуация разделения течений между каждой парой позиций. Каждая пара позиций формирует свое собственное четырехпотоковое течение. Здесь мы не будем предлагать таблицу, а просто продемонстрируем сам подход. Каждый следующий референциал изображается под предыдущим.

Возьмем две смежных открытых референций . Их референциал в алгебре разделения:

по прямому маршруту + = ;

по обратному маршруту + = .

Возьмем теперь два смежных барьера . Их референциал в алгебре разделения:

по прямому маршруту + =

по обратному маршруту + =

Давайте превратим наш последний, чисто референциальный пример, в переномерованный пореграф. Возьмем некоторые три позиции в пореграфе линейной топологии — C, D и E, где установлены следующие смежные референтности: C D E. Здесь мы имеем парно-позиционно-различенную ситуацию: слева в каждой паре — активная позиция. Каков будет в разных алгебрах референциал позиции E для пути C—E? Как можно заметить, между позициями C и D — мембрана «па-от» и «па-до»), а между позициями D и E — экран «па-до»).

Чтобы установить референциал, нам не нужно даже вникать в названия и их различия от разного расположения активных позиций по отношению к пассивной. Можно просто исходить из обозначения самой стрелки: раз путь задан слева направо, то референциал будет определяться правой частью стрелок. Когда путь задан справа налево, референциал будет определяться левой частью стрелок.

В алгебре слияния референциал R позиции E для пути C—E равен . Иначе говоря, RE(C—E) = . Референциал R позиции C для пути E—C равен . То есть RC(E—C) = .

В алгебре поглощения RE(C—E) = и RC(E—C) = .

Референциалы позиции E для пути C—E и позиции C для пути E—C это части референтности, которые могут быть распространены на следующие позиционные отрезки их путей справа E и слева от C.

Для алгебры слияния: C D E

Для алгебры поглощения: C D E

Это не означает, однако, что референтности крайних отрезков слева от позиции C и справа от позиции E будут таковыми, поскольку C и E могут тоже изменять референтность, но они должны будут изменять именно такие изначальные референтности. Если же позиции будут представлять собой полностью открытые референции, то они передадут далее именно такие референциалы. Такое свойство позиционно-референциальных отношений в линейной или сетевой топологии называется референциальным наследованием.

Кроме линейных участков в сети есть также такие, которые представлены нами в виде базовых сетевых локусов. Полный перечень базовых сетевых локусов с точки зрения применения Теории Виртуальности состоит из восьми ситуаций. Однако, когда позиционирование через «АВ»-норму перестает иметь столь фундаментальное значение, перечень сетевых базовых локусов для сетевой позиционно-референциальной алгебры можно уменьшить с восьми до четырех — нераспределенные: рассредоточенный (рисунок 1) и сосредоточенный (рисунок 2); распределенные: светвляющийся (рисунок 3) и разветвляющийся (рисунок 4) локусы. Мы будем рассматривать только локусы, где узел представляет собой активную позицию, а соседние позиции — пассивные.

Давайте рассмотрим некоторый локус. Здесь мы поставим указатели активности так, чтобы если центральная E-позиция как активная была слева по отношению к каждой из позиций C, D, F, то указатели активности оказывались вверху.

Здесь угадывается двойной светвляющийся (C и D светвляются в F, а C и F светвляются в D) и разветвляющийся (C разветвляется в D и F) локус. Референциалы при исчислении сетевого маршрута нужно располагать по ходу самого маршрута, при этом указатель активности может оказываться как внизу, так и вверху, в зависимости от того, как мы смотрим.

Давайте рассчитаем промежуточные и концевые референциалы в алгебре поглощения.

RE(C—E)= 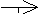; RE(D—E)= ; RE(F—E)= ;

RC(E—C)= ; RD(E—D)= ; RF(E—F)= ;

RC(D—C)= ; RC(F—C)= ; RD(F—D)= ;

RD(C—D)= ; RF(C—F)= ; RF(D—F)= .

Теперь мы можем суммировать любые промежуточные референциалы в концевой для данного маршрута референциал. Например: RE(C—E)+RF(E—F)=RF(C—F), т.е. + = .

Теперь давайте рассчитаем промежуточные и концевые референциалы в алгебре слияния.

RE(C—E)= 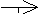; RE(D—E)= ; RE(F—E)= ;

RC(E—C)= ; RD(E—D)= ; RF(E—F)= ;

RC(D—C)= ; RC(F—C)= ; RD(F—D)= ;

RD(C—D)= ; RF(C—F)= ; RF(D—F)= .

Обратите внимание на случаи RD(F—D) и RF(D—F), RC(D—C) и RD(C—D), где происходит соотнесение референциалов с разносторонне заданными указателями активности. Именно наличие указателей активности позволяет соотносить их.

По оценке визуального расположения тетрарных референций и по концевым референциалам можно увидеть, что этот локус представляет собой, скорее всего, разветвляющийся локус для сетевого пути от позиции C через позицию E, являющуюся фильтром «па-от» для сетевых путей к позициям D и F.

Алгебраически-референциальные операции по-разному происходят в нераспределенных и распределенных базовых сетевых локусах. Для нераспределенных сетевых локусов важное значение имеют конечные или начальные референциалы, а для распределенных локусов важное значение имеют не только концевые, но и промежуточные референциалы. Используя предложенную алгебру тетрарных референций, мы можем исчислять любой участок сети любой сетевой топологии с любыми барьерами и получать промежуточные, концевые и конечные референциалы.

Тетрарная референция пореграфов удобна тем, что она позволяет производить интуитивно (глядя на сами стрелки) алгебраические расчеты слияния барьеров на любых линейных путях «АВ»-цепочек на любом участке сети или целой сети.

 

Краткие выводы

 

В предложенных подходах теории пореграфов мы приобрели ряд важных теоретических представлений о бинарных и тетрарных референциях позиционно-референциальных отношений, которые могут иметь линейную и сетевую топологию. Линейную позиционно-референциальную топологию бинарной референции мы использовали для теории коммуникации в работе «Конструирование медиареальности», где также может быть задействована и соответствующая ей позиционно-референциальная алгебра.

Сетевую позиционно-референциальную топологию можно использовать как развитие понимания разомкнутой метрики «АВ»-моделирования в Теории Виртуальности. Интересную проблему представляет вопрос — можно ли использовать тетрарную референцию для «АВ»-моделирования в Теории Виртуальности? Пока таких задач автор не видит.

Кроме того, алгебру линейной и сетевой топологии тетрарной референции можно использовать для оптимизации расчета сетевых маршрутов компьютерных сетей, где есть не просто топологические задачи прокладки кабелей, а необходимость учета разных барьеров в их взаимодействии между различными участками сети, обслуживаемыми разными серверами с разной политикой безопасности.