 |
|
Модуль и фаза комплексного числа
Введение понятия комплексного числа. Представление комплексного числа на плоскости
Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы 
, которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:
 .
| (1) |
В литературе часто мнимую единицу обозначают через 
. Тогда комплексное число 
можно представить в виде:
 ,
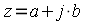| (2) |
где 
носит название действительной части или реальной части и обозначается 
, а 
носит название мнимой части и обозначается как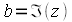 
. Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.
Рисунок 1: Представление комплексного числа на плоскости
Комплексная плоскость 
делится прямыми реальной части 
(прямой действительных чисел) и прямой мнимых чисел 
на четыре четверти. Любое комплексное число 
,будет представляться точкой на комплексной плоскости с координатам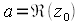и 
и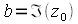 
. Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси .
Модуль и фаза комплексного числа
Если из начала координат комплексной плоскости к точке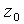 
восстановить вектор, то можно вычислить длину этого вектора как
 .
| (3) |
При этом 
— действительное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно оси на некоторый угол 
, называемый фазой. Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
| (4) |
Тогда комплексное число можно представить в тригонометрической форме
 .
| (5) |
Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа:
 ,
| (6) |
тогда
 ,
| (7) |
где 
учитывает четверть комплексной плоскости в которой расположено число :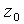
 .
| (8) |
Рисунок 2: Вычисление угла поворота вектора комплексного числа
Для того чтобы понять смысл функции рассмотрим четыре варианта как это показано на рисунке 2.
Рисунок 2.а. , 
и 
, вектор в первой четверти плоскости. В этом случае 
и 
.
Рисунок 2.б. , 
и вектор во второй четверти плоскости. В этом случае 
. Обозначим 
, тогда 
. угол 
находится в четвертой четверти а угол во второй. Для того чтобы получить угол необходимо 
, т.е. 
Рисунок 2.в. , и 
вектор в третьей четверти плоскости. В этом случае 
. Обозначим 
, тогда 
. угол 
находится в первой четверти а угол в третьей. Для того чтобы получить угол необходимо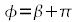 
, т.е. .
Рисунок 2.г. , 
и вектор в четвертой четверти плоскости. В этом случае 
. Обозначим 
, тогда . угол находится как и угол в четвертой четверти следовательно они равны, т.е. 
и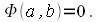 
Функция которая позволяет получить угол c учетом четверти комплексной плоскости в которой расположен вектор называется функция арктангенс-2 и обозначается 
. Функция арктангенс-2 присутсвует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.