 |
|
Та приклад розв’язку
Однією із найважливіших характеристик сукупності є середні. Середньою величиною встатистиці називається узагальнююча характеристика сукупності однотипних явищ за будь-якою кількісно варіюючою ознакою. Середня вказує на розмір цієї ознаки, віднесений до одиниці сукупності.
В залежності від характеру явищ, що вивчаються, завдань та цілей статистичного дослідження, а також від змісту конкретного вихідного матеріалу використовуються слідуючі види середніх величин (таблиця 6.2.1): арифметична  , квадратична
, квадратична 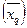 , гармонічна
, гармонічна  , геометрична
, геометрична 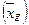 .
.
Таблиця 6.2.1
Види середніх величин
| Прості | Степеневі ← → середні форми | Зважені |
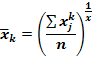
| Загальна формула степеневих середніх | 
|
| Види | ||

| Арифметична k=1 |

|
| Продовження таблиці 6.2.1 | ||

| Гармонічна k=-1 |
 , де , де

|

| Квадратич- на k=2 |
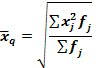
|

| Геометрична k=0 | 
|
Позначення:
 - значення варіант;
- значення варіант;
 - вага або частота;
- вага або частота;
 - загальна чисельність сукупності;
- загальна чисельність сукупності;
k – статистична розмірність ознаки.
Середня арифметична застосовується тоді, коли обсяг варіюючої ознаки утворюється як сума окремих варіант; середня квадратична - коли обсяг варіюючої ознаки утворюється як сума квадратів окремих варіант; середня гармонічна - коли обсяг варіюючої ознаки утворюється як сума обернених значень окремих варіант; середня геометрична - коли об'єм варіюючої ознаки утворюється як добуток окремих варіант.
Середні значення можна знаходити для статистичної сукупності, яка зведена в дискретний чи інтервальний статистичний ряд. При цьому треба зауважити, що інтервальний ряд треба перетворити в дискретний шляхом знаходження середин інтервалів.
Крім того, для інтервальних рядів найбільш раціональним способом пошуку середніх є метод моментів. Метод моментів будується на використанні математичних властивостей середньої арифметичної зваженої - це дозволяє значно спростити техніку розрахунку. Розрахунок проводиться за формулою:
 (6.3)
(6.3)
де 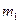 -момент першого порядку; А - стала величина, на яку зменшуються всі значення ознаки.
-момент першого порядку; А - стала величина, на яку зменшуються всі значення ознаки.
В варіаційних рядах з рівними інтервалами, в якості такої величини вибирають варіанту ряду з найбільшою частотою; і — величина інтервалу.
Для більш повної характеристики статистичної сукупності поряд з середніми значеннями ознаки знаходять, так звані, структурні середні - моду і медіану.
Мода  - це варіанта, яка найчастіше зустрічається в статистичному ряді розподілу.
- це варіанта, яка найчастіше зустрічається в статистичному ряді розподілу.
Медіана (Ме) - варіанта, яка ділить ранжований (впорядкований по зростанню чи спаданню значень варіант) ряд розподілу на дві рівні частини, тобто знаходиться в середині варіаційного ряду.
Мода використовується в тих випадках, коли потрібно охарактеризувати найбільш поширену величину ознаки. Медіана цікава тим, що показує кількісну межу значення варіюючої ознаки, якої досягла половина елементів сукупності.
Модою в дискретному варіаційному ряді буде варіанта, що має найбільшу частоту. Можуть бути розподіли, де всі варіанти зустрічаються однаково часто, в такому випадку моди немає або, інакше, можна сказати, що всі варіанти однаково модальні. В інших випадках не одна, а дві варіанти можуть мати найбільші частоти. Тоді будуть дві моди, розподіл буде бімодальним.
Для знаходження медіани в дискретному варіаційному ряді потрібно суму частот поділити пополам і до одержаного результату додати ½. Тоді медіаною буде та варіанта, якій відповідає сума накоплених частот (кумулятивна частота) рівна чи більша значення (Σƒ/2)+½  . Якщо Σƒ/2 - парне число, то (Σƒ/2)+½ - число дробове, а варіанти з дробовим номером не буває. Тому одержаний результат вказує, що медіана знаходиться між Σƒ/2 і (Σƒ/2)+1 варіантами.
. Якщо Σƒ/2 - парне число, то (Σƒ/2)+½ - число дробове, а варіанти з дробовим номером не буває. Тому одержаний результат вказує, що медіана знаходиться між Σƒ/2 і (Σƒ/2)+1 варіантами.
При розрахунку моди і медіани в інтервальному ряді користуються формулами:

де  - мінімальна межа модального інтервалу;
- мінімальна межа модального інтервалу;
 - величина модального інтервалу;
- величина модального інтервалу;
 - частота інтервалу, який передує модальному;
- частота інтервалу, який передує модальному;
 - частота наступного за модальним інтервалу.
- частота наступного за модальним інтервалу.

де 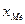 - початкове значення медіанного інтервалу;
- початкове значення медіанного інтервалу;
 - величина медіанного інтервалу;
- величина медіанного інтервалу;
 - сума частот ряду;
- сума частот ряду;
 - сума накопичених частот в інтервалах, які передують медіанному;
- сума накопичених частот в інтервалах, які передують медіанному;
 - частота медіанного інтервалу.
- частота медіанного інтервалу.
Визначення модального і медіанного інтервалів проводиться аналогічно визначенню моди імедіани для дискретного ряду розподілу.
Вивчення статистичної сукупності за допомогою середньої, моди чи медіани не дає повного уявлення про характер розподілу ознаки між одиницями сукупності. Для того, щоб оцінити на скільки середня є типовою для даної статистичної сукупності, застосовують цілий комплекс параметрів, які мають назву показники варіації.
Найбільш поширені показники варіації зведені в таблицю 6.2.2
Дисперсія має математичні властивості, які дозволяють спростити техніку її розрахунку. Найважливішими з них є слідуючі:
1. Якщо від всіх варіант відняти деяке стале число А, те дисперсія від цього не зміниться.

 (6.6)
(6.6)
2. Якщо всі значення варіант поділити на деяку сталу А, то середній квадрат відхилення зменшиться від цього в  разів, а середнє квадратичне відхилення зменшиться в А разів.
разів, а середнє квадратичне відхилення зменшиться в А разів.


 (6.7)
(6.7) 
3. Дисперсія від середньої завжди менше дисперсій розрахованих від будь-яких інших величин, тобто має властивість мінімальності.

Таблиця 6.2.2
Показники варіації
| Показник | Розрахункова формула за даними | Примітка | ||
| Незгрупованими | Згрупованими | |||
Розмах варіації – це різниця між найбільшим 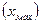 і наймен-шим і наймен-шим  зна-ченням ознаки. Характеризує межі, в яких змінюється значення ознаки зна-ченням ознаки. Характеризує межі, в яких змінюється значення ознаки
|

| В інтервальному ряді розподілу R визначається як різниця між верхньою межею останнього інтер-валу і нижньою межею першого або як різниця між середніми значеннями цих інтервалів. | ||
Середнє лінійне відхилення 
|

|
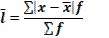
| n - число оди-ниць сукупності; x - значення варі-ант; f- частота;
 - середнє ариф-метичне значення варіюючої озна-ки. - середнє ариф-метичне значення варіюючої озна-ки.
| |
| Продовження таблиці 6.2.2 | ||||
Середнє квадратичне відхилення 
|

|

| R, I, σ мають одиниці виміру варіюючої озна-ки. Чим менша варіація, тим менше значення цих характерис-тик | |
| Середній квад-рат відхилення від середньої арифметичної – дисперсія |
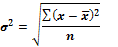
|

|  - безроз-мірна величина і самостійного економічного значення не має; потрібна для розрахунку - безроз-мірна величина і самостійного економічного значення не має; потрібна для розрахунку  . .
| |
| Коефіцієнт варіації: · лінійний · квадратич-ний Коефіцієнт осциляції |



|  -використову-ється для оцінки однорідності су-купності
(надійності і типовості се-редньої вели-чини). Коли -використову-ється для оцінки однорідності су-купності
(надійності і типовості се-редньої вели-чини). Коли  ≤33%, то вважають, що сукупність є однорідною, а середня є типовою. ≤33%, то вважають, що сукупність є однорідною, а середня є типовою.
| ||
На використанні цих властивостей базуються спеціальні методи обчислення дисперсії:
1. Середній квадрат відхилення дорівнює середньому квадрату значень ознаки мінус квадрат середнього значення ознаки, тобто
 (6.8)
(6.8)
2. Метод моментів. Для рядів розподілу з рівними інтервалами дисперсія, розрахована методом моментів, дорівнює квадрату величини інтервалу помноженому на різницю між моментом другого порядку і квадратом моменту першого порядку:
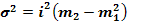 (6.9)
(6.9)

 (6.10)
(6.10)
 (6.11)
(6.11)
А - середина інтервалу (варіанта), якій відповідає найбільша частота,
і - величина інтервалу.
При вивченні варіації тієї чи іншої ознаки доводиться стикатися з необхідністю виявлення, впливу окремих факторів чи умов, що визначають дану варіацію в цілому, Виявити долю варіації визначену окремими факторами можна розбиваючи всю сукупність на групи за фактором (ознакою) вплив якого виймається,
У найпростішому випадку, коли сукупність розділена на групи за однією ознакою, в ній можуть розглядатися:
1. Загальна варіація сукупності, що є результатом дії всіх причин. Ця варіація вимірюється загальною дисперсією  , яка характеризує відхилення індивідуальних значень ознаки сукупності від загальної середньої:
, яка характеризує відхилення індивідуальних значень ознаки сукупності від загальної середньої:
 (6.12)
(6.12)
2. Варіація групових середніх, що відображає відхилення групових середніх від загальної середньої і визначає вплив того фактора, за яким проведене групування. Ця варіація вимірюється міжгруповою дисперсією:
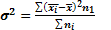 (6.13)
(6.13)
де  - групові середні;
- групові середні;
 - загальна середня для всій сукупності;
- загальна середня для всій сукупності;
 - чисельність окремих груп.
- чисельність окремих груп.
3. Залишкова (або внутрішньогрупова) варіація, що відображає відхилення окремих значень ознаки в кожній групі від їх групової середньої і, відповідно, визначає вплив всіх інших факторів, крім покладеного в основу групування.
Оскільки варіацію в кожній групі відображає групова дисперсія,
 (6.14)
(6.14)
то для всієї сукупності залишкову варіацію визначатиме середня з групових дисперсій, яку називають внутрішньогруповою дисперсією  , і визначають за формулою
, і визначають за формулою
 (6.15)
(6.15)
Очевидно, що загальна варіація ознаки в сукупності повинна визначатися як сума варіації групових середніх ( за рахунок одного виділеного фактора) і залишкової варіації (за рахунок решти факторів), тобто
 (6.16)
(6.16)
Ця рівність відома як правило додавання дисперсій.
Частка від ділення дисперсії групових середніх на загальну дисперсію називається коефіцієнтом детермінації. Він вказує на те, яка доля всієї варіації ознаки обумовлена ознакою покладеною в основу групування.
 (6.17)
(6.17)
Корінь квадратний з коефіцієнта детермінації дає кореляційне відношення (емпіричне), що показує тісноту зв'язку між ознаками групувальними і результативними.
 (6.18)
(6.18)
Ознаки, які мають одні одиниці і не мають інші, називаються альтеративними. Дисперсія альтеративної ознаки  дорівнює добутку долі одиниць, що мають дану ознаку, на доповнююче цю долю до одиниці число:
дорівнює добутку долі одиниць, що мають дану ознаку, на доповнююче цю долю до одиниці число:
 (6.19)
(6.19)
Корінь квадратний з цього показника відповідає середньому квадратичному відхиленню.