Приклади розв’язування задач.

Приклад 3.1. Однорідний ящик, що має форму куба, спирається одним ребром на підлогу, іншим - на вертикальну стіну. Коефіцієнт тертя між підлогою і ящиком, а також між ящиком і стіною дорівнює . При яких значеннях кута між підлогою і гранню ящика можлива його рівновага?

Рис. 3.1

Розв’язок. Це задача на статику твердого тіла, що не має закріпленої осі обертання. Виконуємо рисунок. Вважаючи ребро куба рівним , позначаємо прикладені до нього сили. З боку стінки на нього діють нормальна сила реакції опори і сила тертя спокою , що не дає ящику ковзати по стінці вниз. З боку підлоги на ящик діють реакція опори і сила тертя , що попереджує ковзання куба вправо, з боку Землі – сила тяжіння, рівна 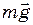, що проходить через центр куба.

Оскільки куб перебуває в стані спокою, сума моментів всіх сил відносно будь-якої точки повинна дорівнювати нулю. Щоб рівняння моментів було якомога простішим, вибираємо точку так, щоб через неї проходило найбільше число ліній дії сил. Такій умові в даній задачі задовольняють шість точок , ,…, . Через кожну з них проходить дві лінії дії сил. Візьмемо одну з них, наприклад, .

Відносно цієї точки моменти сил і дорівнюють нулю, оскільки плечі цих сил відносно точки дорівнюють нулю.

Знаходимо плечі сил 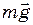, і відносно точки . З трикутників і вони рівні відповідно , і .

Враховуючи, що ящик стоїть під граничним кутом на межі ковзання і, отже, сили тертя спокою мають найбільші значення, рівні, відповідно і , а також знаки моментів, складаємо рівняння моментів:

(1)

З отриманого рівняння ми не можемо знайти кут нахилу, тому потрібно скласти рівняння рівноваги для проекцій.

Проведемо осі координат і , як показано на рисунку, і, оскільки всі сили напрямлені по цих осях, записуємо рівняння рівноваги ящика в проекціях:

На вісь

(2)

На вісь

(3)

Склавши рівняння рівноваги (1) – (3) і розв’язуючи їх відносно невідомого - мінімального кута нахилу ящика до горизонту, отримаємо:

Максимальний кут, під яким може стояти ящик, дорівнює, очевидно, ; таким чином,

Приклад 3.2П’ять куль, маси яких дорівнюють відповідно , , , , і , закріплені на стержні так, що їх центри знаходяться на відстані один від одного. Нехтуючи масою стержня, знайдіть центр ваги системи.

Рис. 3.2

Розв’язок. В основі розв’язку задач на визначення центра ваги системи матеріальних точок (системи тіл з відомим положенням центра ваги кожного тіла) лежить наступна обставина. Якщо в центрі ваги системи частинок, жорстко зв’язаних одна з одною, прикласти вертикально вгору рівнодійну силу , що дорівнює за модулем вазі всіх частинок, то система знаходитиметься в рівновазі. Сума моментів всіх сил (включаючи і рівнодійну силу) повинна в цьому випадку дорівнювати нулю відносно будь-якої точки.

Нехай маси частинок системи дорівнюють , ,….., і положення центра ваги ми будемо відраховувати по горизонталі (вісь ) від центра ваги крайньої лівої частинки (див. рисунок а). Тоді відстань від точки до лінії дії рівнодійної сили - координату центра ваги системи можна знайти з рівняння моментів, складеного відносно точки :

де , , і т.д. – плечі сил , , …, відносно центра ваги лівої частинки. Підставляючи в це рівняння замість модуля рівнодійної сили його вираз і розв’язуючи рівняння відносно , одержимо:

або, коротше:

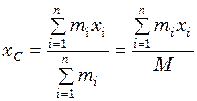де і - маса і координата і-ї частинки; - маса всіх частинок.

Аналогічно знаходиться - координата центра ваги системи матеріальних точок по осі .

Отримані вирази для і є одними з основних формул механіки, які дозволяють визначити координати центра ваги системи матеріальних точок на площині.

Розв’язок нашої задачі ґрунтується на щойно отриманому результаті.

Виконавши рисунок (рис. б), позначаємо всі сили, що діють на систему. Вибираємо точку відліку в центрі першої кулі і на довільній від неї відстані уявно прикладаємо до стержня рівнодійну силу , модуль якої дорівнює модулю сили тяжіння, що діє на всю систему:

Знаходимо плечі всіх сил відносно . Вони дорівнюють відповідно 0, , , та .

Визначаємо положення центра ваги:

Приклад 3.3Визначте положення центра ваги однорідної квадратної пластинки з стороною , в якій вирізано круглий отвір радіусом так, як показано на рисунку.

Рис. 3.3

Розв’язок. На прикладі задачі ми розглянемо, як визначається положення центра ваги однорідних плоских фігур, що мають отвір. Елементарними методами ці задачі розв’язуються тільки при умові, що положення центра ваги цілої фігури і центра тяжіння вирізаної частини відомо.

В задачах цього типу фігуру з отвором бажано зобразити так, щоб вісь симетрії була горизонтальна. В основі виведення розрахункового співвідношення лежить наступна обставина, що має загальний характер. Якщо вставити вирізану частину пластинки на попереднє місце, то силу тяжіння всього тіла, що рівна 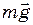(в даній задачі квадрата), можна представити як суму двох паралельних сил – сили тяжіння вирізаної частини (диска), що дорівнює , і сили тяжіння фігури, що залишилася (квадрата з отвором), що дорівнює 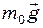. Перша з цих сил прикладена в центрі ваги не вирізаної фігури (квадрата), друга – в центрі ваги вирізаної частини (круга), третя – в невідомому поки що центрі тяжіння пластинки з отвором. Якщо відомі рівнодійна сила ( 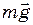), одна з паралельних сил ( ) і відстань між лініями дії цих сил, легко встановити положення лінії дії другої сили ( 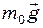), а отже і відстань між центрами ваги вирізаної і цілої фігур. Дійсно, відносно точки повинно бути

або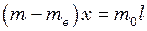

оскільки модуль сили тяжіння фігури, що залишилася, дорівнює:

З попередньої рівності знаходимо:

або остаточно:

Оскільки маса однорідної пластинки однакової товщини дорівнює , де - площа; - густина матеріалу.

В даній задачі площа вирізаної частини , площа всієї фігури 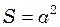. Відстань між центрами тяжіння вийнятого диска і квадрата дорівнює:

Підставляючи в розрахункову формулу числові значення, отримаємо:

Приклад 3.4На який кут нахилиться автомобіль при гальмуванні? Центр мас автомобіля розташований посередині колісної бази на висоті м на д землею, відстань між осями коліс , коефіцієнт тертя ковзання , пружність всіх чотирьох пружин підвіски однакова і така,, що їх прогин у нерухомого автомобіля см.

Вказівка: вважати, що гальмуються всі колеса.

Рис. 3.4

Розв’язок. При гальмуванні автомобіль нахиляється вперед (див. рисунок), внаслідок додаткового моменту сил тертя ковзання відносно центра мас .

В неінерціальній системі відліку, пов’язаній з автомобілем, суми проекцій всіх сил (сили тяжіння, реакцій опори, тертя і інерції) на вертикальну і горизонтальну координатні осі дорівнюють нулю, тобто

, ,

Крім того, сума моментів всіх сил відносно будь-якої точки, в тому числі і відносно точок опори 1 і 2, дорівнюють нулю, тобто

З цих рівнянь знаходимо величини сил реакцій опори:

, (1)

За умовою у нерухомого автомобіля всі пружини підвіски стиснуті на 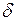і тому , де - коефіцієнт жорсткості кожної пружини. При гальмуванні пружини передньої підвіски додатково стискаються на величину , а стиснення задніх пружин зменшується на , як показано на рисунку. Тоді, якщо знехтувати вагою коліс, умови рівноваги в ресорах запишуться так:

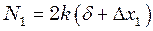, (2)

Порівнюючи формули (1) і (2), знаходимо:

або

Як видно з рисунку:

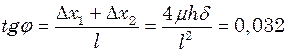, звідки .

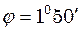Рис. 3.5

Приклад 3.5Вільний кінець ланцюжка масою і довжиною , що висів вертикально, прикріпили до стелі так, що ланцюжок провисає під стелею на відстань . Знайти силу натягу ланцюжка в точці , що в початковому стані знаходилася на тій же відстані від стелі.

Розв’язок. Виділимо нескінченно малий елемент ланцюжка довжиною і масою 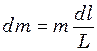. Прикладені до його кінців сили натягу напрямлені по дотичній до ланцюжка і різні за величиною.