Главная | Обратная связь

Теоретические основы

Лабораторная работа №1

Исследование характеристик дифференцирующей цепи

 

1. Цель работы: овладение методами измерения основных характеристик линейной цепи (звена).

 

Теоретические основы

 

Дифференцирующей называется электрическая цепь, в которой выходная величина пропорциональна производной от входной величины. Простейшими дифференцирующими цепями могут служить цепи с емкостью или индуктивностью (рис.2.1).

 

Рис.2.1 Простейшие дифференцирующие цепи

В цепи с емкостью

 

Принимая u_c (t) за входную величину, а ток i_c (t) – за выходную, получим дифференцирующую цепь.

В цепи с индуктивностью

Принимая i_L(t) за входную величину, а u_L(t) – за выходную, получим дифференцирующую цепь.

Использовать ток как входную или выходную величину практически затруднительно, так как в первом случае необходимо иметь стабильный источник тока, а во втором для его измерения необходимо включить последовательно дополнительное сопротивление, которое оказывает влияние на процесс. Следовательно, входной и выходной величинами целесообразно выбирать напряжения, при этом используются rC - и rL – цепи. На практике широкое распространение получила rC - цепь.

 

Условие, при котором rC-цепь выполняет операцию дифференцирования, вытекает из уравнения

Если принять

то

При синусоидальном входном напряжении уравнение цепи в комплексной форме

 

По условию дифференцирования

тогда

 

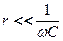или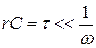

При несинусоидальной форме напряжения U₁(t) условие дифференцирования должно быть выполнено для всех гармонических составляющих входного сигнала. При этом условием дифференцирования является

где ω_В – частота наивысшей гармоники, которой нельзя пренебречь.

 

Идеальное дифференцирование прямоугольного импульса показано на рис. 2.2,а. Амплитуда выходного сигнала u₂(t)бесконечно велика.

 

 

Рис.2.2 Идеальное (а) и реальное (б) дифференцирование прямоугольного импульса

 

График напряжения u₂(t)на выходе реальной дифференцирующей цепи показан на рис.2.2,б. Напряжение u₂(t)представляет собой импульсы экспоненциальной формы с чередующейся полярностью.

За длительность выходного импульса принимают время, равное утроенному значению постоянной времени цепи . Амплитуда импульсов равна величине входного напряжения. Сравнение временных диаграмм реальной и идеальной дифференцирующей цепи (рис.1,а и 1,б) показывает, что при уменьшении τдлительность импульсов u₂(t)сокращается и кривая u₂(t)стремится по форме к производной входного напряжения. Величина τ называется постоянной времени цепи и соответствует изменению выходного напряжения на 63% от исходного (e^-1 = 0.37). Очевидно, что время изменения выходного напряжения зависит от сопротивления резистора и емкости конденсатора и, соответственно, постоянная времени цепи пропорциональна этим значениям, т. е. τ = RC (в секундах).

Дифференцирующая цепь называется еще укорачивающей, так как длительность выходных импульсов значительно меньше, чем входных.

 

Допустим, конденсатор разряжен. При подаче на вход RC-цепи импульса напряжения конденсатор сразу же начнет заряжаться током, проходящим через него самого и резистор. Сначала ток будет максимальным, затем по мере увеличения заряда конденсатора постепенно уменьшится до нуля по экспоненте. Когда через резистор проходит ток, на нем образуется падение напряжения, которое определяется, как U=i R, где i-ток заряда конденсатора. Поскольку ток изменяется экспоненциально, то и напряжение будет изменяться также - экспоненциально от максимума до нуля. Падение напряжения на резисторе как раз и является выходным, величину которого можно определить по формуле U_вых = U₀e^-t/τ.

Передаточная функция цепи (коэффициент передачи) - равна отношению комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе:

, где - фазово-частотная характеристика, - амплитудно-частотная характеристика цепи.

Импульсная характеристика g(t) -реакция цепи на действие сигнала в виде δ-функций, т. е. это сигнал на выходе, если сигнал на входе есть d-функция. при . При этом g(t) = 0 при t < 0 – выходной сигнал не может возникнуть ранее момента появления входного сигнала.

Импульсная характеристика цепи и передаточная функция связаны преобразованием Фурье:

Переходная характеристика цепи h(t) - является откликом на сигнал, называемый единичным скачком: h(t) = 1 при t >0, h(t) = 0 при t < 0, при этом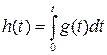

Для дифференцирующей цепи:

Комплексный коэффициент передачи: ,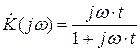

Передаточная функция:

ФЧХ: ; АЧХ:

Импульсная характеристика:

Рис.2.3 АЧХ (а) и ФЧХ (б) идеального дифференциатора

Условие хорошего дифференцирования сигнала: для синусоидального колебания с частотой w дифференцирование осуществляется при условии, что частота его много меньше величины 1/RC. Если на входе действует сложный сигнал, то он будет хорошо дифференцироваться, если наивысшая частота в спектре входного сигнала много меньше граничной частоты цепочки.

Подставляя в выражение для передаточной функции K(p) вместо р комплексную величину jω, мы получаем однозначную зависимость между передаточной функцией и частотными характеристиками звена. При этом комплексная величина K(jω) есть функция частоты, и называется амплитудно-фазовой характеристикой (АФХ). При построении K(jω) в прямоугольной системе координат - комплексной плоскости - получаем годограф амплитудно-фазовой характеристики, где частота ω входит как параметр. Примерный вид годографа АФХ показан на рис. 2.4. Каждой точке такого годографа соответствует определенная частота ω, как и помечено на рисунке.

Рис.2.4 Амплитудно-фазовая характеристика

 

АФЧХ реального дифференцирующего звена приведена на рис. 2.5.

Рис.2.5 Годограф АФЧХ реального дифференцирующего звена

 

Годограф описывает полуокружность с радиусом, стремящимся к ¥ при T стремящимся к 0. При этом годограф прижимается к положительной мнимой полуоси и становится практически неотличим от годографа идеального дифференцирующего звена.

Частота w*=1/T считается максимальной, при которой еще реальное дифференцирующее звено работает "почти как идеальное". При достаточно низких частотах реальное дифференцирующее звено близко к идеальному.