 |
|
Тригонометрическая форма числа
Глава 2
Комплексные числа
Понятие комплексных чисел
Основные понятия
Комплексным числом zназывается выражение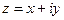 
, где x и y – действительные числа, i – мнимая единица, которая определяется соотношением:
При этом число a называется действительной частью числа z: x = Re z (Real), а y- мнимой частью:y = Im z (Imaginary).
Множество комплексных чисел обозначается С.
Если x =Re z =0, то число z будет чисто мнимым, если y = Im z = 0, то число z будет действительным.
Числа 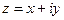и 
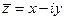называются комплексно – сопряженными.
Свойства комплексного сопряжения.
1°. 
.
2°. 
.
3°. Если 
, то 
.
4°. 
.
5°. 
– вещественное число.
Два комплексных числа 
и 
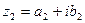называются равными, если соответственно равны их действительные и мнимые части:
Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части ( 
)
1.2. Геометрическая интерпретация комплексных чисел.
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа.
Пусть на плоскости задана прямоугольная система координат. Тогда 
Cможно поставить в соответствие точку на плоскости с координатами 
. Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые − на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.
Отметим, что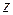 
и 
симметричны относительно оси Oy, а 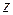и 
симметричны относительно Ox.
Каждому комплексному числу (т.е. каждой точке на плоскости) можно поставить в соответствие вектор с началом в точке O и концом в точке . Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу 
, обозначается той же буквой 
Длина вектора 
соответствующего комплексному числу , равна 
, причем 
, 
.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа
Наряду с длиной 
вектора 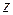введем в рассмотрение угол 
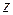между вектором и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается 
. Угол определяется не однозначно, а с точностью 
… . Для 
аргумент не определяется.
При этом
 ,  .
| (1) |
Следовательно, любое комплексное число 
можно представить в виде
 .
| (2) |
Формулы (2) задают так называемую тригонометрическую форму записи комплексного числа.
Из (1) следует, что если 
и 
то
 ,  .
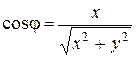| (3) |
Из (1) 
что по и комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу 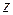его модуль находится однозначно, а аргумент 
, в силу (3), − с точностью 
. Также из (3) следует, что аргумент может быть найден как решение уравнения
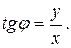
Однако не все решения этого уравнения являются решениями (3).
Среди всех значений аргумента комплексного числа выбирается одно, которое называется главным значением аргумента и обозначается 
. Обычно главное значение аргумента выбирается либо в интервале 
, либо в интервале 
В тригонометрической форме удобно производить операции умножения и деления.
Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.
