 |
|
Примеры решения задач по теме «Комплексные числа»
Пример 1.Вычислить 
Решение. Преобразуем данное выражение следующим образом:
Приведем комплексное число, стоящее в числителе к тригонометрической форме:
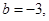
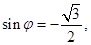следовательно, 
и 
Воспользуемся формулой Муавра: 
Совершенно аналогично преобразуем выражение, стоящее в знаменателе: приведем комплексное число, стоящее в знаменателе к тригонометрической форме:
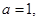
следовательно, 
и 
Воспользуемся формулой Муавра:
После этих преобразований наше выражение принимает вид:
В последнем выражении воспользуемся формулой деления комплексных чисел, записанных в тригонометрической форме, тогда имеем:
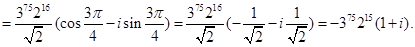
Пример 2. Решить уравнение x3+1+i=0.
Решение.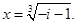 
Найдем тригонометрическую форму комплексного числа, стоящего под знаком корня:
следовательно, 
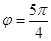и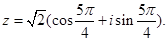 
Используя формулу извлечения корня n-ой степени из комплексного числа, получим:
где 
Подставляя значения k в последнюю формулу, получим три различных корня:
k=0, 
k=1, 
k=2, 
Пример 3.Решить уравнение x2+24-10i=0.
Решение. X2= -24+10i. Если x=a+bi, где a и b действительные числа, то x2= =-24+10i =(a+bi)2=a2-b2+2abi. Таким образом, сравнивая действительные и мнимые части, получим: a2-b2=-24, ab=5.
Решим полученную систему из двух уравнений с двумя неизвестными. Из второго уравнения выразим b и подставим в первое, тогда
b=5/a, a2-25/a2=-24.
Обозначив a2=v, получим квадратное уравнение v2+24v-25=0, из которого находим v1=-25, v2=1. Но так как a - вещественное число, то v 
0, значит, v=1, т. е. a= 
1 и b= 5. Тогда имеем два значения корня в алгебраической форме: x1=1+5i, x2=-1-5i.
Проверка: x12=x22=1-25+10i=-24+10i.
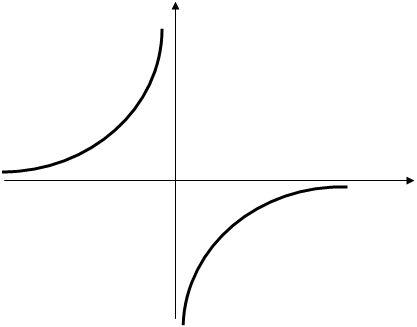
Пример 4.Найти и изобразить множество точек комплексной плоскости, удовлетворяющих условию Im(z2)=-2.
Решение. Пусть z=x+iy, тогда Im(z2)=2xy=-2, т. е. данным условием задается множество точек комплексной плоскости, лежащих на гиперболе, заданной уравнением xy=-1.
 |
Imz
0 Rez
Пример 5.Найти и изобразить множество точек комплексной плоскости, удовлетворяющих условию Rez+Imz=4.
Решение. Пусть z=x+iy, тогда данное выражение принимает вид x+y=4, т. е. множеством точек комплексной плоскости, удовлетворяющих условию Rez+Imz=4, являются все точки, расположенные на прямой x+y=4. Изобразим это на графике:
Im z
0 4 Re z
Пример 6.Найти и изобразить множество точек комплексной плоскости, удовлетворяющих условиям
.
Решение. Вычислив целую часть, получим следующую систему
.
Определим, какое множество точек комплексной плоскости задает неравенство системы:
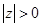- это все точки комплексной плоскости, кроме точки 0 (Imz=0, Rez=0);
- это внутренность круга с центром в точке 0, радиуса r=1, включая границу круга, т. е. окружность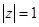 
.
Двойное неравенство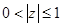 
, таким образом, задает множество точек комплексной плоскости, лежащих внутри круга и на его границе, но не включая центр круга (точку 0).
- это множество точек комплексной плоскости, лежащих на луче, исходящем из точки 0 и составляющем с положительной частью действительной оси Rez угол 200 по положительному направлению отсчета углов.
Таким образом, искомым множеством будет пересечение найденных множеств, т. е. часть луча, исходящего из точки 0 и составляющего с положительной частью действительной оси угол 200 по положительному направлению отсчета углов, содержащаяся внутри круга , исключая саму точку 0. Изобразим это на графике:
 |
Imz
1
1 Rez
Пример 7. Выразить cos10x, sin10x через cosx и sinx.
Решение. Рассмотрим сумму z= cos10x+isin10x. Тогда по формуле Муавра, имеем: cos10x+isin10x=( cosx+isinx)10. Используя формулу бинома Ньютона:
,
получим
Выделим мнимую и действительную части, тем самым получим искомые ответы.
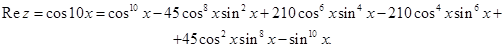
Замечание. Аналогичным образом можно найти cosnx, sinnx, используя формулы Муавра и бинома Ньютона. Действительно:
cosnx+isinnx=(cosx+isinx)n,
,
.
Пример 8. Найти суммы
S(x)=sinx-sin2x+…+sin99x, T(x)=cosx-cos2x+…+cos99x.
Решение. Вычислим сумму T(x)+iS(x).
T(x)+iS(x)=(cosx+isinx)-(cos2x+isin2x)+…+(cos99x+isin99x).
По формуле Муавра имеем:
T(x)+iS(x)=(cosx+isinx)-(cosx+isinx)2+…+(cosx+isinx)99.
Обозначим cosx+isinx=a и воспользуемся формулой n-го члена геометрической прогрессии, тогда
.
Учитывая наше обозначение и используя формулу Муавра, получим:
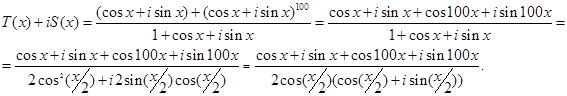
Умножим в полученном равенстве числитель и знаменатель на число, сопряженное знаменателю и раскроем скобки, используя формулу умножения комплексных чисел в тригонометрической форме:
Преобразуем полученное выражение, используя формулы суммы косинусов двух аргументов и суммы синусов двух аргументов, тогда
Таким образом, мы получили следующие значения искомых сумм:
