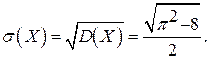Главная | Обратная связь

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

 

Функция распределения или плотность распределения полностью описывают случайную величину. Часто, однако, при решении практических задач нет необходимости в полном знании закона распределения, достаточно знать лишь некоторые его характерные черты. Для этого в теории вероятностей используются числовые характеристики случайной величины, выражающие различные свойства закона распределения. Основными числовыми характеристиками являются математическое ожидание, дисперсия и среднее квадратическое отклонение.

Математическое ожиданиехарактеризует положение случайной величины на числовой оси. Это некоторое среднее значение случайной величины, около которого группируются все ее возможные значения.

Математическое ожидание случайной величины X обозначают символами М(Х)или т. Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных значений случайной величины на вероятности этих значений:

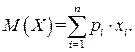
Математическое ожидание непрерывной случайной величины определяется с помощью несобственного интеграла:

Исходя из определений, нетрудно убедиться в справедливости следующих свойств математического ожидания:

1. (математическое ожидание неслучайной величины с равно самой неслучайной величине).

2. Если 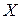³0, то ³0.

3. .

4. Есл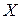и и независимы, то .

Пример 3.3. Найти математическое ожидание дискретной случайной величины, заданной рядом распределения:

X
p	0.2	0.4	0.3	0.1

Решение.

=0×0.2 + 1×0.4 + 2×0.3 + 3×0.1=1.3.

Пример 3.4. Найти математическое ожидание случайной величины, заданной плотностью распределения:

.

Решение.

Дисперсия и среднее квадратическое отклонениеявляются характеристиками рассеивания случайной величины, они характеризуют разброс ее возможных значений относительно математического ожидания.

Дисперсией D(X) случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания Для дискретной случайной величины дисперсия выражается суммой:

(3.3)

а для непрерывной – интегралом

(3.4)

Дисперсия имеет размерность квадрата случайной величины. Характеристикой рассеивания, совпадающей по размерности со случайной величиной, служит среднее квадратическое отклонение.

Свойства дисперсии:

1) – постоянные. В частности,

2)

3)

В частности,

(3.5)

Заметим, что вычисление дисперсии по формуле (3.5) часто оказывается более удобным, чем по формуле (3.3) или (3.4).

Величина называется ковариацией случайных величин .

Если , то величина

называется коэффициентом корреляции случайных величин .

Можно показать, что если , то величины линейно зависимы: где

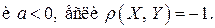
Отметим, что если независимы, то

и

Пример 3.5. Найти дисперсию случайной величины, заданной рядом распределения из примера 1.

Решение. Чтобы вычислить дисперсию, необходимо знать математическое ожидание. Для данной случайной величины выше было найдено: m=1.3. Вычисляем дисперсию по формуле (3.5):

Пример 3.6. Случайная величина задана плотностью распределения

Найти дисперсию и среднее квадратическое отклонение.

Решение. Находим сначала математическое ожидание:

(как интеграл от нечетной функции по симметричному промежутку).

Теперь вычисляем дисперсию и среднее квадратическое отклонение: