 |
|
Тема 4. Елементи комбінаторики в теорії ймовірностей: переставлення, розміщення та комбінації
Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів.
У противному разі множину називають невпорядкованою.
Переставлення.Переставленням із 
елементів називають такі впорядковані множини із елементів, які різняться між собою порядком їх розміщення.
Кількість таких упорядкованих множин обчислюється за формулою
, (3)
де набуває лише цілих невід’ємних значень.
Оскільки 
, то при 
маємо 1! = 0! Отже, 0! =1.
Приклад 1.На кожній із шести однакових карток записано одну з літер
Я, І, Р, Е, О,Т.
Яка ймовірність того, що картки, навмання розкладені в рядок, утворять слово
| Т | Е | О | Р | І | Я |
Розв’язання. Кількість усіх елементарних подій (елементів множини 
)
Кількість елементарних подій, що сприяють появі слова ТЕОРІЯ, m = 1. Позначивши розглядувану подію через В, дістанемо:
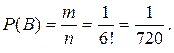
Приклад 2.Задано множину цілих чисел 
Її елементи навмання розставляють у рядок. Обчислити ймовірності таких випадкових подій:
A – розставлені в ряд числа утворюють зростаючу послідовність;
B – спадну послідовність;
C – цифра 1 стоятиме на першому місці, а 5 – на останньому ;
D – цифри утворять парне п’ятицифрове число.
Розв’язання. Простір елементарних подій для цього експерименту міститиме 
несумісних, рівно ймовірних елементарних подій.
Кількість елементарних подій, що сприяють появі А, дорівнює одиниці 
.
Кількість елементарних подій, що сприяють появі В, дорівнює одиниці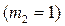 
.
Для випадкової події С 
Для випадкової події D 
Обчислюємо: 
Розміщення.Розміщенням із елементів по 
називаються такі впорядковані множини, кожна із яких містить 
елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.
Кількість таких множин обчислюється за формулою
(4)
Наприклад, 
Приклад 1.Маємо дев’ять однакових за розміром карток, на кожній з яких записано одну з цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9. Навмання беруть чотири картки і розкладають в один рядок. Яка ймовірність того, що при цьому дістанемо
Розв’язання. Кількість елементарних подій множини буде 
Кількість елементарних подій, що сприяють появі 1, 9, 7, 3, дорівнює одиниці 
. Позначимо цю випадкову подію через В. Тоді
Приклад 2.У кімнаті перебувають 10 студентів. Яка ймовірність того, що два і більше студентів не мають спільного дня народження?
Розв’язання. Вважаємо, що рік має 365 днів. Для кожного студента в загальному випадку існує 365, а для 10 студентів – 36510 можливих днів народження. Отже, маємо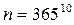 
елементарних подій множини . Позначимо через В випадкову подію, яка полягає в тому, що дні народження студентів не збігаються. Кількість елементарних подій, що сприяють появі В, 
Остаточно маємо: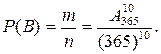 
Комбінації.Комбінаціями з елементів по називаються такі множини з 
елементів, які різняться між собою хоча б одним елементом.
Кількість таких множин
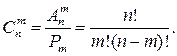(5)
Приклад 1.У цеху працює 10 верстатів-автоматів, кожний із яких може з певною ймовірністю перебувати в робото здатному стані або в стані поломки. Яка ймовірність того, що під час роботи верстатів-автоматів із ладу вийдуть три з них?
Розв’язання. Оскільки кожний верстат-автомат може перебувати у двох несумісних станах – робото здатному або не робото здатному, то кількість усіх елементарних подій множини буде 
Позначимо через А випадкову подію – із ладу вийде три верстати з десяти. Тоді кількість елементарних подій, що сприяють появі А, буде
Отже, 
Приклад 2.У шухляді міститься 10 однотипних деталей, 6 із яких є стандартними, а решта бракованими. Навмання із шухляди беруть чотири деталі. Обчислити ймовірність таких випадкових подій:
А – усі чотири деталі виявляються стандартними;
В – усі чотири деталі виявляються бракованими;
D – із чотирьох деталей виявляються дві стандартними і дві бракованими.
Розв’язання. Кількість усіх елементарних подій множини
кількість елементарних подій, що сприяють події А:
кількість елементарних подій, що сприяють появі В:
кількість елементарних подій, що сприяють появі D:
Обчислимо ймовірності цих подій:
При розв’язуванні задач комбінаторики використовуються такі правила:
Правило суми.Якщо деякий об’єкт 
може бути відібраний із сукупності об’єктів k способами, а другий об’єкт 
може бути відібраний s способами, то відібрати або , або можна k + s способами.
Правило добутку.Якщо об’єкт можна вибрати із сукупності об’єктів k способами і після кожного такого відбору об’єкт можна вибрати s способами, то пара об’єктів 
у зазначеному порядку може бути вибрана 
способами.
Задача.Банк протягом місяця може видати в кредит позику п’ятьом своїм клієнтам, у той час як поступили замовлення на кредит від 15 клієнтів першого району і 10 клієнтів другого району. Для збереження клієнтів банк розглядає як тимчасову вимушену міру – розігрування випадковим чином п’яти позик серед тих, від кого поступило замовлення. Знайти ймовірність того, що число клієнтів першого району, яким дістанеться позика, дорівнює: а) 5; б) 0; в) 3.
Випробування – проведення розігрування серед клієнтів банку. Наслідок випробування – п’ятірка клієнтів. Число наслідків випробування дорівнює числу все можливих п’ятірок, які можна утворити із сукупності чисельністю 25 елементів (клієнтів банку).
Для таких груп елементів характерним є те, що вони відрізняються одна від одної хоча б одним елементом. Крім того, як основна сукупність елементів (з 25 клієнтів), так і утворені групи по 5 елементів складаються з різних елементів (відсутність повторів). Це дає підстави зробити висновок, що такі групи є комбінаціями. І їх число для всіх трьох підзадач дорівнює:
а) А – власниками кредиту є п’ять клієнтів першого району. Число наслідків випробування, для яких відбудеться подія А, дорівнює числу всеможливих п’ятірок клієнтів, котрі можна утворити із загального числа 15 клієнтів першого району. Ці п’ятірки знову є комбінаціями і їх загальне число
За класичним означенням ймовірності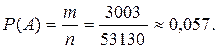 
б) В – власниками кредиту є п’ять клієнтів другого району. Число наслідків випробування , для яких відбудеться подія В, дорівнює числу всеможливих п’ятірок клієнтів, що можна утворити із 10 клієнтів другого району. Знову ж ці п’ятірки є комбінаціями і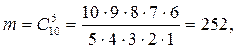 
а 
в) С – власниками кредиту є три клієнти першого району і два клієнти другого району. Всеможливі трійки першого району можна утворити 
способами, а все можливі двійки клієнтів другого району - 
. Використавши правило добутків, отримаємо 
звідки 