 |
|
Теорема Четаева о неустойчивости
Если уравнения возмущённого движения таковы, что можно указать ограниченную в области  функцию
функцию  , принимающую в некоторой области
, принимающую в некоторой области  вместе со своей производной значения одного знака, обращающуюся в нуль в начале координат и такую, что при всех значениях
вместе со своей производной значения одного знака, обращающуюся в нуль в начале координат и такую, что при всех значениях  выполняются неравенства
выполняются неравенства  , то тривиальное решение рассматриваемой системы неустойчиво.
, то тривиальное решение рассматриваемой системы неустойчиво.
Доказательство.В области  выберем начальные значения
выберем начальные значения  , такие что
, такие что  , где
, где  - сколь угодно мало. Покажем, что как бы мало ни были числа
- сколь угодно мало. Покажем, что как бы мало ни были числа  , наступит момент времени
, наступит момент времени  , когда по крайней мере одна из величин
, когда по крайней мере одна из величин  . (т.е. изображённая точка покинет окрестность
. (т.е. изображённая точка покинет окрестность  ).
).
Т.к. при  , то имеем
, то имеем

Но при условии  согласно условию теоремы имеем
согласно условию теоремы имеем  . Интегрируя, найдём
. Интегрируя, найдём 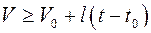 . Т.о. если предположить, что не наступит
. Т.о. если предположить, что не наступит  , когда изображающая точка покинет
, когда изображающая точка покинет  - окрестность, то придётся допустить, что
- окрестность, то придётся допустить, что  . Последнее противоречит условию теоремы об ограниченности V.
. Последнее противоречит условию теоремы об ограниченности V.
Примеры.
1.)Вращение тела с неподвижной точкой в случае Эйлера вокруг одной из главных осей инерции.
Запишем уравнения Эйлера

Рассмотрим частное решение  , соответствующее вращению вокруг оси
, соответствующее вращению вокруг оси  . Составим уравнения возмущённого движения, положив
. Составим уравнения возмущённого движения, положив 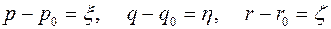 .
.

В качестве функции Ляпунова возьмём функцию
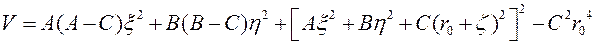 ,
,
которая при  и
и  будет определённо положительной. Составим производную от неё в силу уравнений возмущённого движения
будет определённо положительной. Составим производную от неё в силу уравнений возмущённого движения

Согласно теореме Ляпунова, вращение вокруг меньшей оси устойчиво. Аналогично доказывается устойчивость вращения вокруг вертикальной оси с наибольшим моментом инерции, т.е. случай  . В этом случае функция Ляпунова следует взять в виде
. В этом случае функция Ляпунова следует взять в виде 

2) Неустойчивость вращения вокруг вертикальной оси, для которой  . Применим теорему Четаева. Возьмём функцию Четаева V в виде
. Применим теорему Четаева. Возьмём функцию Четаева V в виде  . Найдём производную
. Найдём производную

В области  и
и 
 определим отрицательной при любых значениях
определим отрицательной при любых значениях  .
.
Согласно теореме Четаева следует неустойчивое вращение вокруг средней оси эллипсоида инерции.
 Замечание.
Замечание.  - знакопостоянна (во всей окрестности), а не знакоопределённа, как требуется в теореме Ляпунова. Действительно, при
- знакопостоянна (во всей окрестности), а не знакоопределённа, как требуется в теореме Ляпунова. Действительно, при  , т.е. эта функция удовлетворяет теореме Ляпунова.
, т.е. эта функция удовлетворяет теореме Ляпунова.
Лекция 10.
§ Обращение теоремы Лагранжа.
Как мы видим, теорема Лагранжа даёт лишь достаточный критерий устойчивости равновесия, утверждая, что устойчивость имеет место лишь при наличии изолированного минимума у потенциальной энергии системы в положении равновесия. Т.о. ничего не говорится об устойчивости или неустойчивости в случае отсутствия такового. При этом отсутствию минимума может соответствовать либо наличие изолированного максимума, либо наличие минимакса.
В связи с этим, начиная с самого Лагранжа, усилия многих механиков было направлено на доказательство неустойчивости равновесия при отсутствии минимума. Эта задача и называется задачей об обращении теоремы Лагранжа. В общем виде эта задача до сих пор не разрешена. Мы здесь рассмотрим два случая обращения, данные Ляпуновым и Четаевым.
Теорема Ляпунова. Если в положении равновесия консервативной механической системы потенциальная энергия имеет изолированный максимум и это определяется совокупностью членов наинизшего порядка в разложении потенциальной энергии в ряд, то равновесии неустойчиво.
Итак, пусть мы имеем механическую систему со стационарными связями, и, следовательно,

а потенциальная энергия имеет вид

где, например,

Для того, чтобы максимум потенциальной энергии определялся по членам наинизшего порядка, т.е. по форме  , последняя должна быть определённо отрицательной функцией (мы будем предполагать, что все координаты обращаются в нуль в положении равновесия). Тогда по доказанной ранее лемме для знакоопределённых форм функция П в достаточно малой окрестности равновесия будет также знакоопределенной отрицательной.
, последняя должна быть определённо отрицательной функцией (мы будем предполагать, что все координаты обращаются в нуль в положении равновесия). Тогда по доказанной ранее лемме для знакоопределённых форм функция П в достаточно малой окрестности равновесия будет также знакоопределенной отрицательной.
Разлагая коэффициенты  в ряд по степеням
в ряд по степеням  в положении равновесия, получим
в положении равновесия, получим
 , где
, где 
Постоянные  обозначим через
обозначим через  , а весь остальной ряд через
, а весь остальной ряд через  . Очевидно все
. Очевидно все  уничтожаются в начале координат и при достаточно малых по модулю
уничтожаются в начале координат и при достаточно малых по модулю  могут быть сделаны сколь угодно малыми. Итак,
могут быть сделаны сколь угодно малыми. Итак,

Для доказательства неустойчивости возьмём функцию Ляпунова в виде

и составим её полную производную в силу дифференциальных уравнений Лагранжа

Получим

Из уравнений Лагранжа имеем  и, следовательно, первая сумма даст
и, следовательно, первая сумма даст

Используя ещё теорему Эйлера, будем иметь

Подставляя это в выражение для  , получим
, получим


В механике доказывается, что форма  - определённо положительная и, следовательно, выбором достаточно малой окрестности начала координат
- определённо положительная и, следовательно, выбором достаточно малой окрестности начала координат  можно всё выражение {…}, входящее в
можно всё выражение {…}, входящее в  , сделать знакоопределённой (положительным) функцией скоростей. Такой же будет и функция
, сделать знакоопределённой (положительным) функцией скоростей. Такой же будет и функция  , а, значит, все выражение для
, а, значит, все выражение для  будет определённо положительной функцией.
будет определённо положительной функцией.
Поскольку выражение

является знакоопределённой функцией, то и саму функцию  можно сделать положительной и, следовательно, на основании теоремы Ляпунова заключить о неустойчивости равновесия.
можно сделать положительной и, следовательно, на основании теоремы Ляпунова заключить о неустойчивости равновесия.
Теорема Четаева. Если в положении равновесия консервативной системы потенциальная энергия не имеет минимума и является формой произвольной степени, то положение равновесия неустойчиво.
Для простоты доказательства перейдём от фазовых переменных  к каноническим сопряжённым переменными
к каноническим сопряжённым переменными  . Тогда при стационарных связях кинетическая энергия будет квадратичной формой обобщённых импульсов
. Тогда при стационарных связях кинетическая энергия будет квадратичной формой обобщённых импульсов 
 .
.
Как и в предыдущем случае, представим кинетическую энергию в виде

где по-прежнему  - постоянные, а
- постоянные, а  - уничтожаются в положении равновесия.
- уничтожаются в положении равновесия.
Тогда функция Гамильтона будет  , где
, где
 .
.
Рассмотрим функцию 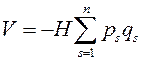 .
.
Т.к. по условию 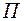 не имеет максимума, то
не имеет максимума, то 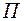 может принимать отрицательные значения. Тогда в окрестности начала координат фазового пространства
может принимать отрицательные значения. Тогда в окрестности начала координат фазового пространства  обязательно существует область, где
обязательно существует область, где
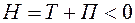
для чего надо взять импульсы настолько малыми, чтобы  . В области выполнения этого неравенства выделим ещё область, где
. В области выполнения этого неравенства выделим ещё область, где  , что всегда возможно сделать, придавая соответствующие значения переменным
, что всегда возможно сделать, придавая соответствующие значения переменным  . Итак, в области
. Итак, в области  будем иметь
будем иметь  . Те же неравенства, взятые со знаком равенства, определяют границу области
. Те же неравенства, взятые со знаком равенства, определяют границу области  .
.
Составим производную от V в силу уравнений Гамильтона
 ,
,  .
.
Получим


Используем теперь полученное ранее выражение для 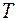
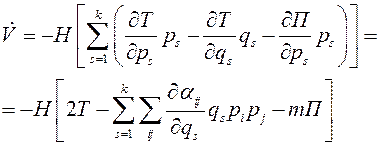

Первые слагаемые в квадратных скобках представляют по доказанному выше определённо-положительную функцию импульсов  , а величина
, а величина  в выбранной области. Поскольку в выбранной области
в выбранной области. Поскольку в выбранной области  , то
, то  является знакоопределённой положительной функцией в этой области и, следовательно, условия теоремы Четаева выполнены.
является знакоопределённой положительной функцией в этой области и, следовательно, условия теоремы Четаева выполнены.
Пример

 ,
,  ;
;
 ,
, 
Тогда неравенство  определит область
определит область  . Область
. Область  ограниченна слева и снизу осями
ограниченна слева и снизу осями  и
и  . Пунктирной линией показана область одновременного выполнения неравенств
. Пунктирной линией показана область одновременного выполнения неравенств  ,
,  .
.
Можно доказать и более общее предложения, также принадлежащие Четаеву:
Если в положении равновесия консервативной механической системы потенциальная энергия, являющаяся аналитической функцией координат, не имеет минимума, то положение равновесия неустойчиво.
Примечание. Все доказанные предложения применимы и к неустойчивости стационарных движений, если исходная система является гироскопически несвязанной. В этом случае в качестве потенциальной энергии должна фигурировать измененная потенциальная энергия – потенциал Рауса.
Т.о. можно сказать, что если потенциал Рауса является аналитической функцией позиционных координат, то наличие минимума для рассматриваемого состояния стационарного движения является необходимым и достаточным условием устойчивости стационарного движения.
Пример Устойчивость круговых орбит стационарного спутника.
Потенциал Рауса в этой задаче имеем вид
 ,
, 
и являлся аналитической функцией координат при условии 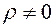 . Раскладывая его в ряд по степеням возмущений
. Раскладывая его в ряд по степеням возмущений
 ,
, 
получим


где 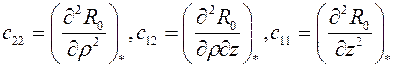
Необходимые и достаточные условия знакоопределённости квадратичной формы, стоящей в квадратных скобках, привели нас к неравенствам
 ,
,  ,
,
которые выражали условия положительности диагональных миноров дискриминанта формы  . Из этих неравенств вытекает одно
. Из этих неравенств вытекает одно  . Невыполнение его означает, что квадратичная форма знакопеременна, несмотря на знак
. Невыполнение его означает, что квадратичная форма знакопеременна, несмотря на знак  (а значит таковым будет и весь ряд
(а значит таковым будет и весь ряд  ).
).
Наличие maxim у квадратичной формы определяется неравенствами
 и
и 
что означает:  и
и  , что невозможно. Следовательно, здесь теорема Ляпунова об обращении неприменима.
, что невозможно. Следовательно, здесь теорема Ляпунова об обращении неприменима.
При отсутствии min форма  знакопеременна, что означает
знакопеременна, что означает  а
а  . Всевозможные варианты знаков такие:
. Всевозможные варианты знаков такие:
1. 
2.  - невозможен
- невозможен
3, 4.  - знакопеременность
- знакопеременность 
Из двух последних вытекает, что при отсутствии min  следует неустойчивость.
следует неустойчивость.
К тому же заключению можно придти, рассматривая уравнения в вариациях для позиционных координат  и
и 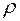 . В этом случае функция Рауса, заменяющая формулу Лагранжа имеет вид
. В этом случае функция Рауса, заменяющая формулу Лагранжа имеет вид
 , где
, где  ,
, 
Составим уравнения в вариациях, полагая  . Разлагая в ряд функцию Рауса
. Разлагая в ряд функцию Рауса  , получим
, получим
 , где
, где

 ...
...
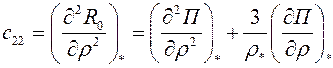 ,
, 
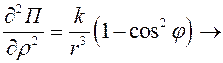


 (в случае минимума)
(в случае минимума)

Из уравнений  , получим
, получим
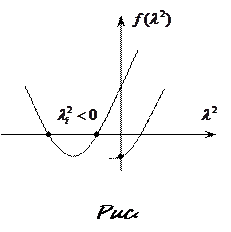
 ,
, 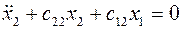 .
.
Полагая  , будем иметь
, будем иметь

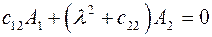

В случае минимума 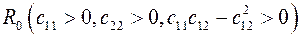 относительно
относительно  многочлен имеет два отрицательных
многочлен имеет два отрицательных  корня и, следовательно, относительно
корня и, следовательно, относительно  будет две пары чисто мнимых корней. В случае
будет две пары чисто мнимых корней. В случае  многочлен имеет вид
многочлен имеет вид  и независимо от знаков
и независимо от знаков  и
и 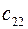 (т.е. либо maxim, либо знакопеременность) обязательно имеет один положительный (относительно
(т.е. либо maxim, либо знакопеременность) обязательно имеет один положительный (относительно  ) корень, и, следовательно, положительный корень относительно
) корень, и, следовательно, положительный корень относительно  .
.
Но 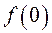 есть дискриминант квадратичной формы
есть дискриминант квадратичной формы  , и, следовательно, условие
, и, следовательно, условие  является необходимым и достаточным условием устойчивости для уравнений первого приближения. Оно является необходимым и достаточным для полных уравнений, т.к. его невыполнение означает отсутствие минимума.
является необходимым и достаточным условием устойчивости для уравнений первого приближения. Оно является необходимым и достаточным для полных уравнений, т.к. его невыполнение означает отсутствие минимума.
Заметим, что исследование по первому приближению не только является более громоздким, но ещё и ничего не говорит apriory о неустойчивости при учёте нелинейных членов.
Лекция 11.
Критерии устойчивости по первому приближению для установившихся
движений.
При рассмотрении уравнений возмущённого движения для установившихся движений

где  не зависят от времени, а
не зависят от времени, а 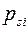 - некоторые постоянные, интересно поставить задачу: когда из устойчивости (неустойчивости) укороченной системы
- некоторые постоянные, интересно поставить задачу: когда из устойчивости (неустойчивости) укороченной системы
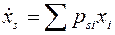
можно судить об устойчивости (неустойчивости) некоторой системы. Интерес к этой задаче прежде всего объясняется тем, что линейные уравнения всегда могут быть проинтегрированы и, следовательно, для них задача об устойчивости может быть разрешена. Однако может оказаться, что задача об устойчивости нулевого решения для линеаризованной системы может не иметь ничего общего с задачей об устойчивости для исходной системы.
Ляпуновым впервые были установлены строгие критерии устойчивости исходной системы по устойчивости линеаризованной системы. Им же было показано, что в ряде случаев, которые он назвал особенными или критическими, задача об устойчивости исходной системы не решается с помощью линеаризованных уравнений. Прежде чем прийти к доказательству и формулированию этих критериев рассмотрим свойства решений линеаризованной системы.
§1. Уравнения первого приближения.
Как известно, для получения решения этих уравнений необходимо рассмотреть определитель
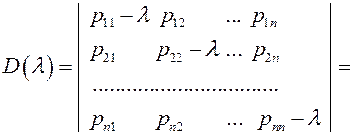

Здесь  - коэффициенты
- коэффициенты  являющиеся функциями постоянных
являющиеся функциями постоянных 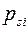 . Решение этого уравнения даст и значения для
. Решение этого уравнения даст и значения для  :
:  , среди которых могут быть кратные. Если все
, среди которых могут быть кратные. Если все  - различные, то мы получим
- различные, то мы получим  частных решений вида
частных решений вида


где постоянные  удовлетворяет системе уравнений
удовлетворяет системе уравнений


Общее решение системы запишется в виде
 ,
, 
В случае кратных корней частные решения системы имеют более сложный вид. Пусть один из корней  имеет
имеет  -ую кратность. Тогда ему кроме указанного решения
-ую кратность. Тогда ему кроме указанного решения

будут отвечать частные решения вида

где  - полиномы от
- полиномы от  , степень которых не превышает
, степень которых не превышает  . Построение всех частных решений такого рода зависит от ранга определителя при значении
. Построение всех частных решений такого рода зависит от ранга определителя при значении  . Пусть ранг этого определителя
. Пусть ранг этого определителя  , т.е. не обращается в нуль по крайней мере один из миноров
, т.е. не обращается в нуль по крайней мере один из миноров  порядка. Тогда все
порядка. Тогда все  частных решений получаться по формулам
частных решений получаться по формулам
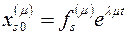




Все эти частные решения линейно независимы. Говорят, что в этом случае кратному корню  отвечает одна группа решений.
отвечает одна группа решений.
Может, однако, оказаться, что для рассматриваемого кратного корня все миноры  порядка определителя
порядка определителя 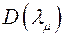 равны нулю. Пусть хотя бы один минор
равны нулю. Пусть хотя бы один минор  -го порядка не обращаются в нуль. Тогда все решения, соответствующие этому корню состоят из двух видов частных решений, получаемых из выражений
-го порядка не обращаются в нуль. Тогда все решения, соответствующие этому корню состоят из двух видов частных решений, получаемых из выражений
 и
и 
где  и
и  - полиномы от
- полиномы от  степеней
степеней  и
и  , причём
, причём  . Среди чисел
. Среди чисел  (и
(и  ) обязательно есть хотя бы одно (назовём его соответственно
) обязательно есть хотя бы одно (назовём его соответственно  и
и  ), наибольшее, такое что
), наибольшее, такое что  . Отсюда следует, что в каждой строчке
. Отсюда следует, что в каждой строчке

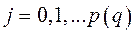
есть хотя бы одно 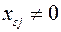 .
.
Таким образом, всего в двух группах будет 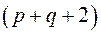 решений. Но поскольку
решений. Но поскольку  , то всего решений оказывается
, то всего решений оказывается  . Все решения получаются следующим образом
. Все решения получаются следующим образом





Таким образом, и в этом случае корни  отвечают
отвечают  частных решений, но они распадаются на 2 группы.
частных решений, но они распадаются на 2 группы.
Если миноры до  - го порядка (не считая самого
- го порядка (не считая самого  - го) обращаются в нуль, то корню
- го) обращаются в нуль, то корню  будет соответствовать
будет соответствовать  подобных групп решений. Очевидно, число
подобных групп решений. Очевидно, число  не может превышать кратности корня
не может превышать кратности корня  . В этом случае каждая группа будет иметь по одному решению вида
. В этом случае каждая группа будет иметь по одному решению вида



Все  групп решений можно записать в виде (
групп решений можно записать в виде (  )
)

Число таких групп равно  , т.е.
, т.е.  . В каждой группе имеется
. В каждой группе имеется 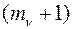 частных решений с наивысшей степенью многочлена
частных решений с наивысшей степенью многочлена  , причём
, причём

При  (т.е. когда не обращается в нуль лишь миноры
(т.е. когда не обращается в нуль лишь миноры  порядка) получаем
порядка) получаем  групп решений. В каждой группе по одному решению с наивысшей степенью многочлена, равной нулю, т.е.
групп решений. В каждой группе по одному решению с наивысшей степенью многочлена, равной нулю, т.е.  решений вида
решений вида
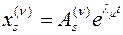 ,
, 
Все приведённые рассуждения справедливы как для вещественных, так и для мнимых корней. Если корни комплексно сопряжённые, т.е.  , то все
, то все 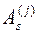 , а также функции
, а также функции  будут комплексно-сопряжёнными
будут комплексно-сопряжёнными
 ,
, 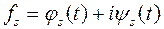
Тогда, в случае простых корней, решение будет вида
 ,
,  ,
, 
В случае кратных корней эти решения будут

Из указанного анализа легко сделать заключение об устойчивости нулевого решения линейной системы.
1. Вещественные части всех корней отрицательны (  ).
).
В этом случае все координаты  при
при  невзирая на кратность корней ибо функция вида
невзирая на кратность корней ибо функция вида

при любой степени полинома  является исчезающей при
является исчезающей при  . Следовательно модули всех
. Следовательно модули всех  стремятся к нулю. Движение асимптотически устойчиво.
стремятся к нулю. Движение асимптотически устойчиво.
2. Среди корней  есть по крайней мере один с положительной вещественной частью.
есть по крайней мере один с положительной вещественной частью.
Пусть  ,
, 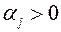 . Тогда по крайней мере одна из функций
. Тогда по крайней мере одна из функций  для соответствующего частного решения будет по модулю неограниченно возрастать при
для соответствующего частного решения будет по модулю неограниченно возрастать при  , поскольку хотя бы в одной паре
, поскольку хотя бы в одной паре  и
и  есть отличные от нуля. Это безграничное возрастание будет при любых начальных условиях (и при сколь угодно малых).
есть отличные от нуля. Это безграничное возрастание будет при любых начальных условиях (и при сколь угодно малых).
3. Характеристическое уравнение имеет нулевые корни или чисто мнимые (т.е. с нулевыми вещественными частями) с числом групп решений, равным кратности корней. При этом вещественные части других корней могут быть отрицательны. Тогда система будет иметь частные решения вида (для нулевых корней)
 ,
, 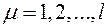 ,
,  - кратность корня
- кратность корня
или вида (для корней вида  )
)

Общее решение системы будет линейной комбинацией постоянных  или тригонометрических функций. Отсюда следует что при достаточно малых по модулю начальных возмущениях (а, следовательно, и малых констант
или тригонометрических функций. Отсюда следует что при достаточно малых по модулю начальных возмущениях (а, следовательно, и малых констант  ) модули возмущений
) модули возмущений  во всё последующее время также не будет превышать сколь угодно малых по модулю чисел
во всё последующее время также не будет превышать сколь угодно малых по модулю чисел  .
.
4. Характеристическое уравнение, не имея корней с положительными вещественными частями, имеет кратные нулевые или чисто мнимые корни с числом групп решений, меньшим их кратности. Тогда при нулевых корнях будут частные решения вида.
 , где
, где  полиномы степени
полиномы степени 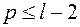 (
(  - кратность коня), а при чисто мнимых решения вида
- кратность коня), а при чисто мнимых решения вида

Отсюда видно, что какими бы малыми мы ни выбирали начальные значения  при
при  , модули
, модули  будут неограниченно возрастать и, следовательно, нулевое решение будет неустойчиво.
будут неограниченно возрастать и, следовательно, нулевое решение будет неустойчиво.
Пример: Двойной нулевой корень.
Рассмотрим две системы уравнений
1)  2)
2) 
В первом случае характеристический определитель будет (  )
)
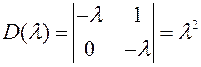 ;
; 
Подставляя это значение  в каждый из миноров первого порядка, видим, что один из них не равен нулю, т.е. ранг
в каждый из миноров первого порядка, видим, что один из них не равен нулю, т.е. ранг  равен
равен  . Следовательно, в этом случае двойному нулевому корню будет соответствовать только одна группа частных решений, имеющая вид
. Следовательно, в этом случае двойному нулевому корню будет соответствовать только одна группа частных решений, имеющая вид
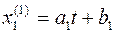 ,
, 
 ,
, 
Подставляя это решение в уравнение, найдём, что  ,
,  . Итак
. Итак
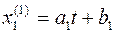 ,
, 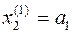
 ,
, 
Числа  и
и  могут выполнять роль произвольных постоянных. Очевидно
могут выполнять роль произвольных постоянных. Очевидно  ,
,  и, если
и, если  , то при
, то при  модуль
модуль  будет неограниченно возрастать. Следовательно, в этом случае движение неустойчиво.
будет неограниченно возрастать. Следовательно, в этом случае движение неустойчиво.
По-другому обстоит дело во втором случае. Здесь характеристический определитель имеет вид
 ,
, 
Все миноры  первого порядка (
первого порядка (  -го) равны нулю и, следовательно ранг определителя равен
-го) равны нулю и, следовательно ранг определителя равен 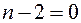 . Число групп решений, соответствующее указанному нулевому корню будет равно его кратности. Общее решение системы имеет вид
. Число групп решений, соответствующее указанному нулевому корню будет равно его кратности. Общее решение системы имеет вид  ,
,  , в котором
, в котором 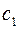 и
и  представляют начальные значения координат
представляют начальные значения координат  и
и 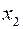 . Эти значения могут быть выбраны меньше любого заданного малого числа
. Эти значения могут быть выбраны меньше любого заданного малого числа  и, следовательно, движение устойчиво, но не асимптотически.
и, следовательно, движение устойчиво, но не асимптотически.
Из проведённого исследования приходим к заключению, что вопрос об устойчивости линейной системы полностью определяется характером корней определяющих уравнения. Мы можем сформулировать следующие предложения.
1. Для асимптотической устойчивости тривиального решения линейной системы необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательны.
2. Если среди корней есть хотя бы один с положительной вещественной частью, то тривиальное решение неустойчиво.
3. Тривиальное решение будет устойчиво, но не асимптотически, если характеристическое уравнение, не имея корней с положительными вещественными частями, имеет корни с нулевыми вещественными частями, если эти корни простые, а, если они кратные, то число групп решений должно быть равно их кратности.
4. Тривиальное решение неустойчиво, если число групп решений, соответствующим кратным корням с нулевыми вещественными частями, меньше их кратности.
Таким образом, для решения вопроса об устойчивости линейной системы не нужно знать самих корней, а достаточно лишь определить знаки вещественных частей.
§2. Критерий отрицательности вещественной части корней
характеристического уравнения.
Наиболее общие критерии отрицательных вещественных частей были получены Раусом и Гурвицом. Это критерии получаются в виде неравенств, накладываемых на коэффициенты характеристического уравнения. Для уравнения

составим матрицу, в которой по диагонали стоят коэффициенты  до
до  , а в сторонах соответственно коэффициенты с нечётными и чётными индексами. Если рядом стоящий номер превышает
, а в сторонах соответственно коэффициенты с нечётными и чётными индексами. Если рядом стоящий номер превышает  или должен быть отрицательным, то соответственно элемент заменяется на 0.
или должен быть отрицательным, то соответственно элемент заменяется на 0.

Чтобы все корни имели отрицательные вещественные части необходимо и достаточно, чтобы все диагональные миноры (при  ) были положительными, т.е.
) были положительными, т.е.
 ,
,  ,
,  ,
, 
Если знак хотя бы одного из миноров при  будет отрицательным , то среди корней есть хотя бы один с положительной вещественной частью. Можно также показать, что для выполнения указанных неравенств необходимо, чтобы все коэффициенты
будет отрицательным , то среди корней есть хотя бы один с положительной вещественной частью. Можно также показать, что для выполнения указанных неравенств необходимо, чтобы все коэффициенты  были положительными (но этого недостаточно), т.е. если среди
были положительными (но этого недостаточно), т.е. если среди  есть хотя бы один отрицательный, то вещественные части всех корней не могут быть отрицательны.
есть хотя бы один отрицательный, то вещественные части всех корней не могут быть отрицательны.
Рассмотрим частные случаи.
I. Система 1-го порядка.
 ,
,  ,
,  (
(  !)
!)
II. Система 2-го порядка
 ,
, 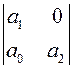 Диагональные миноры:
Диагональные миноры:

 , т.е.
, т.е.  ,
, 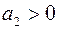 .
.
III. Система 3-го порядка


Диагональные миноры:
 ,
,  ,
, 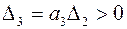 , следовательно
, следовательно 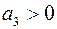 .
.
Окончательно получаем
 ,
,  ,
, 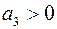 .
.
IV. Система 4-го порядка.

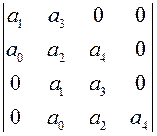
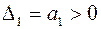 ,
, 
 ,
, 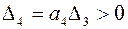 , отсюда
, отсюда  .
.
Если использовать условия 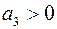 , то неравенство
, то неравенство  становится следствием неравенства
становится следствием неравенства  . Т.о. для этого случая можно записать
. Т.о. для этого случая можно записать
 ,
, 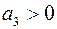 ,
,  ,
, 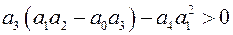 ,
, 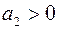 .
.
Использование критерия Гурвица для  приводит к быстро нарастающей громоздкости неравенств и практически становиться мало удобным. При больших
приводит к быстро нарастающей громоздкости неравенств и практически становиться мало удобным. При больших  используется ЭВМ и некоторые другие методы (метод
используется ЭВМ и некоторые другие методы (метод  - разбиваний, критерий Михайлова и т.д.)
- разбиваний, критерий Михайлова и т.д.)
Пример 1. Определить область асимптотической устойчивости для параметров  и
и  системы уравнений.
системы уравнений.
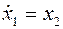 ,
,  ,
, 
Составим характеристический определитель  :
:

Раскрывая по элементам 1-ой строки, получим
 или
или  .
.
Все коэффициенты положительны, следовательно, условия необходимые выполнены. Составим матрицу Гурвица

Отсюда находим  ;
;  ,
, 

Область асимптотической устойчивости имеет вид: см. рис. 34.
Пример 2.
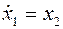 ,
,  ,
,  ,
, 





По Гурвицу должны выполняться неравенства  ,
,  ;
;  .
.
Из последнего неравенства имеем  . Что невозможно при положительном
. Что невозможно при положительном  и
и  .
.
Матрица Гурвица: 
 .
.
Лекция 12.
§ Теоремы Ляпунова об устойчивости по первому приближению.
Рассмотрим нелинейную систему уравнений возмущённого движения

где  - некоторые аналитические функции, разложение которых в ряды по
- некоторые аналитические функции, разложение которых в ряды по  начинаются членами не ниже первого порядка, т.е.
начинаются членами не ниже первого порядка, т.е.  .
.
Доказанные в предыдущем параграфе теоремы позволяют сформулировать необходимые и достаточные условия устойчивости нелинейной системы на основании рассмотрения только свойств решений уравнений первого приближения, т.е. уравнений
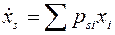 .
.
Имеют место следующие теоремы об устойчивости по первому приближению.
Теорема 1. Если все корни характеристического уравнения имеют отрицательные вещественные части, то невозмущённое движение асимптотически устойчиво, каковы бы ни были члены высших порядков в уравнениях возмущённого движения.
Теорема 2. Если среди корней характеристического уравнения системы первого приближения есть хотя бы один с положительно вещественной частью, то тривиальные решения неустойчиво при любом выборе членов выше первого порядка в уравнениях возмущённого движения.
Устойчивость по первому приближению
I. Устойчивость. Рассмотрим случай различных корней. Пусть первые  пар комплексно сопряжённые
пар комплексно сопряжённые

 , а остальные вещественные
, а остальные вещественные

 .
.
Пусть все  и
и  .
.
Тогда всю систему можно записать в виде
 ,
, 



где  - комплексно-сопряжённые переменные, а
- комплексно-сопряжённые переменные, а  - вещественные;
- вещественные;  и
и  - нелинейные члены, представимые рядами.
- нелинейные члены, представимые рядами.
Рассмотрим определённо положительную функцию
 .
.
Её производная  равна
равна

 .
.
Величина  - вещественная, и, значит такова же
- вещественная, и, значит такова же ⇐ Предыдущая12