 |
|
Алгоритм простого деления
Алгоритмы формирования таблиц простых чисел
Цель работы
Освоить современные методы и базовые алгоритмы формирования таблиц простых чисел.
Порядок выполнения работы
1. Повторить основные термины арифметики и теории чисел, связанные с понятиями простого, составного и взаимно-простого числа, разложением числа на множители, кратностью.
2. Провести поиск в Интернет и в литературных источниках, найти понятие и описание способов получения таблиц простых чисел. В качестве базовых предлагаются методы простого перебора (простого деления); алгоритмы Эратосфена; Сундарама и Аткина. Можно предложить иной современный или самостоятельно разработанный алгоритм.
3. Используя выбранный (по таблице вариантов или самостоятельно найденный) алгоритм, составить таблицу простых чисел для заданного интервала и подсчитать их количество.
3. Подготовить отчет, содержащий:
1) Титульный лист
2) Введение (о применении простых чисел в защите информации);
3) Основной раздел, в котором:
- дать определения всем перечисленным в п.1 понятиям (простое число, составное число, число кратное заданному и т.д.);
- словесно описать схему получения таблиц простых чисел выбранным методом;
- составить алгоритм (отобразить блок-схему) формирования таблицы простых чисел для заданного интервала и подсчета количества таких чисел;
- привести программу работы алгоритма (выбор языка - произвольный);
- показать результаты работы программы, сформировать таблицу простых чисел в заданном интервале (от m до n) и подсчитать их количество;
- определить количество операций сложения (вычитания) и умножения (деления) либо сдвига, необходимых для получения результата (вычислительную сложность метода), отразить в отчете.
4) Выводы.
Таблица 1. Варианты заданий
| № п\п | m | n | Базовый алгоритм |
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена | |||
| Сундарама | |||
| Аткина | |||
| перебора | |||
| Эратосфена |
Алгоритмы поиска простых чисел (базовые сведения)
Решето Эратосфена
Вполне вероятно, что алгоритм, придуманный более 2000 лет назад греческим математиком Эратосфеном Киренским, был первым в своем роде. Его единственная задача – нахождение всех простых чисел до некоторого заданного числа N. Термин «решето» подразумевает фильтрацию, а именно фильтрацию всех чисел за исключением простых. Так, обработка алгоритмом числовой последовательности оставит лишь простые числа, все составные же отсеются.
Рассмотрим в общих чертах работу метода. Дана упорядоченная по возрастанию последовательность натуральных чисел. Следуя методу Эратосфена, возьмем некоторое число P изначально равное 2 – первому простому числу, и вычеркнем из последовательности все числа кратные P: 2P, 3P, 4P, …, iP (iP≤N). Далее, из получившегося списка в качестве P берется следующее за двойкой число – тройка, вычеркиваются все кратные ей числа (6, 9, 12, …). По такому принципу алгоритм продолжает выполняться для оставшейся части последовательности, отсеивая все составные числа в заданном диапазоне.
В приведенной таблице записаны натуральные числа от 2 до 100. Красным помечены те, которые удаляются в процессе выполнения алгоритма «Решето Эратосфена».
Программная реализация алгоритма Эратосфена потребует:
1. организовать логический массив и присвоить его элементам из диапазона от 2 до N логическую единицу;
2. в свободную переменную P записать число 2, являющееся первым простым числом;
3. исключить из массива все числа кратные P2, ступая с шагом по P;
4. записать в P следующее за ним не зачеркнутое число;
5. повторять действия, описанные в двух предыдущих пунктах, пока это возможно.
Обратите внимание: на третьем шаге мы исключаем числа, начиная сразу с P2, это связано с тем, что все составные числа меньшие P будут уже зачеркнуты. Поэтому процесс фильтрации следует остановить, когда P2 станет превышать N. Это важное замечание позволяет улучшить алгоритм, уменьшив число выполняемых операций.
Так будет выглядеть псевдокод алгоритма:
P←2
пока P2≤N выполнять
{
i←P2
если B[P]=true то
пока i≤N выполнять
{
B[i]←false
i←i+P
}
P←P+1
}
Он состоит из двух циклов: внешнего и внутреннего. Внешний цикл выполняется до тех пор, пока P2 не превысит N. Само же P изменяется с шагом P+1. Внутренний цикл выполняется лишь в том случае, если на очередном шаге внешнего цикла окажется, что элемент с индексом P не зачеркнут. Именно во внутреннем цикле происходит отсеивание всех составных чисел.
Решето Эратосфена для выявления всех простых чисел в заданной последовательности ограниченной некоторым N потребует O(Nlog (log N)) операций. Поэтому уместнее использовать данный метод чем, например, наиболее тривиальный и затратный перебор делителей.
Решето Сундарама
Решето Сундарама – алгоритм поиска всех простых чисел в некотором заданном диапазоне. Он был разработан в 1934 году ныне безызвестным студентом из Индии С. П. Сундарамом.
Принцип работы алгоритма Сундарама сводится, как и в его знаменитом предшественнике, к последовательному отсеиванию всех ненужных чисел. Но у него есть одна небольшая особенность: результатом работы алгоритма будет последовательность простых чисел из диапазона от 2 до удвоенного значения граничного числа. Допустим необходимо получить все простые числа до некоторого N, тогда выходными данными будут все простые числа от 2 до 2N+1.
Решето Сундарама из ряда натуральных чисел, не превышающих N, исключает числа вида 2ij+i+j. Результат данного выражения, ни при каких значениях входящих в него переменных, не превышает N (2ij+i+j≤N). Соблюдая это условие, а также то, что i всегда меньше или равно j, переменные i и j пробегают все натуральные значения из множеств:

После исключения всех ненужных чисел необходимо увеличить каждое оставшиеся число в два раза и прибавить единицу (2i+1). Итоговое множество будет содержать числа: 2, 3, …, 2N+1.
Решето Аткина.
Описание алгоритма:
Алгоритм состоит из следующих шагов.
1. Выписываются все натуральные числа из диапазона от 1 до n.
2. Перебираются все возможные пары чисел x, y, где x<=sqrt(n) и y<=sqrt(n). Т.е. (1,1), (1,2),…, (1,sqrt(n)), (2,1), (2,2),…, (sqrt(n),sqrt(n)).
3. Для каждой пары чисел вычисляются значения следующих трех уравнений:
a) 4*x^2+y^2;
b) 3*x^2+y^2;
c) 3*x^2-y^2, значение вычисляется только при x>y.
4. Для каждого вычисленного значения уравнений вычисляются остатки от деления на 12, причем
a) если остаток равен 1 или 5 для значения первого уравнения;
b) если остаток равен 7 для значения второго уравнения;
с) если остаток равен 11 для значения третьего уравнения.
То в исходном ряду чисел от 1 до n число помечается как простое.
Замечание: если какое-то число Z присутствует в значениях нескольких уравнений (допустим a и b), и остаток от деления на 12 этого числа удовлетворяет условиям обоих групп, то число помечается два раза: сначала как простое, а потом как составное.
5. На последнем этапе проверяется кратность помеченных чисел квадратам простых чисел из диапазона от 5 до sqrt(n). Если число кратно квадрату, то оно помечается как составное.
Пример работы алгоритма для n = 40.
1. Выписываем все натуральные числа из диапазона от 1 до 40.

2. Перебираются все возможные пары чисел от (1,1) до (6,6) (Т.к. sqrt(40) ~ 6).
2. Вычисляем значения уравнений для каждой пары чисел x и y.

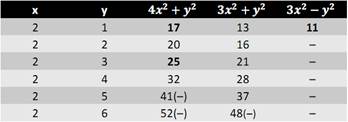

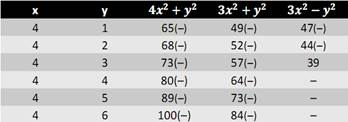
4. Вычисляем остаток от деления на 12 и помечаем простые числа.

5. Проверяем кратность помеченных чисел квадратам простых из диапазона от 5 до 6.
5 — простое число, 6 — составное, значит проверяем на кратность 5^2=25 помеченные числа. В результате 25 — нужно вычеркнуть. В итоге остаются только простые числа от 1 до 40.

Алгоритм имеет асимптотическую сложность  и требует
и требует  бит памяти. На входных значениях порядка
бит памяти. На входных значениях порядка 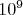 решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до
решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до 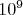 :
:

В результате можно наблюдать следующую скорость выполнения:
| 10 000 000 | 0.15 сек. |
| 100 000 000 | 2.16 сек. |
| 1 000 000 000 | 48.76 сек. |
Алгоритм простого деления
Описание алгоритма:
(http://algolist.manual.ru/maths/teornum/factor/trial.php)
Это самый простой, наивный метод - метод простого деления. Практически при любом алгоритме факторизации оптимально использовать этот способ до некоторой границы B, чтобы убрать малые делители.
Наиболее наивный подход - просто делить на все числа подряд до корня из N.
Пусть мы хотим поделить N на все простые числа до корня из N. Для этого мы можем иметь или не иметь в своем распоряжении достаточно большую таблицу простых чисел. Если это не так, то, очевидно, мы можем делить N на числа d в заданных классах эквивалентности, например, 1 и 5 по модулю 6, или 1,7,11,13,17,19,23,29 по модулю 30. Тогда мы проделаем много бессмысленных делений (на составные числа), однако результат останется верным. Таким образом, можно составить следующий алгоритм:
Предположим, что у нас уже есть таблица простых чисел: p[1] = 2, p[2] = 3, ... , p[k], где k > 3, массив t := [6,4,2,4,2,4,6,2], и индекс j, такой что если p[k] mod 30 равно 1,7,11,13,17,19,23 или 29, то j := 0,1,2,3,4,5,6 или 7 соответственно.
Выберем некоторую верхнюю грань B, такую что B >= p[k], чтобы не тратить на этот алгоритм слишком много времени.
Получив на входе положительное целое число N, этот алгоритм пытается разложить его на множители, и, если это не получается, то N - число без простых делителей, меньших либо равных B.
1. [Инициализация]
Если N <= 5, вывести разложение 1 = 1, 2 = 2, 3 = 3, 4 = 22, 5 = 5 в зависимости от N и выйти. Иначе, i := -1, m := 0, L := [ N1/2 ]
2. [Cледующее простое]
Пусть m := m + 1. Если m > k, то i : = j - 1 и идти к шагу 5, иначе d : = p[m].
3. [Простое деление]
Пусть r : = N mod d. Если r = 0, то вывести d как нетривиальный делитель N и выйти ( или N := N / d, L : = [ N1/2 ] и повторить шаг 3, если мы хотим продолжить нахождение делителей N).
4. [Простое?]
Если d >= L, то в случае N > 1 вывести сообщение, что оставшаяся часть N - простое и выйти. Иначе, если i < 0 идти на шаг 2.
5. [Следующий делитель]
Пусть i := i + 1 mod 8, d := d + t[i]. Если d > B, то вывести сообщение о том, что оставшиеся простые делители N больше B, иначе идти на шаг 3.
Заметим, что i = -1 пока мы используем нашу таблицу простых и i >= 0 если нет.
Метод весьма полезен для удаления малых множителей, однако его не следует использовать для полной факторизации, кроме тех случаев, когда N - очень маленькое ( например, N < 108).