Пересечение и объединение множеств.

Упражнение 1.

А) Объясните, из каких элементов состоят множества N, Z, Q, R.

Б) Назовите несколько чисел, являющихся элементами для каждого множества.

В) Назовите числа, которые являются элементами одного из множеств и не являются

элементами остальных трёх.

Г) Нарисуйте диаграмму, показывающую взаимосвязь этих множеств между собой.

Решение.

В) Такие элементы есть только во множестве R. Например, ÎR , но ÏN, ÏZ, ÏQ. Элементы любого из множеств N, Z, Q обязательно входят и в множество R.

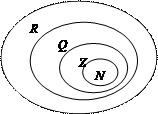Г) N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

R – множество действительных чисел.

Учителю. Рассматривая материал, мы не выходим за множество действительных чисел.

Задание 1. Задайте множество:

А) учителей математики вашей школы;

Б) нечётных чисел;

В) корней уравнения х² + 5 = 0;

Г) решений неравенства х > 4;

Ответ: Б) {х çх = 2n - 1; n Î Z }; В) Æ; Г) (4; +¥).

Учителю. При необходимости можно повторить запись числовых множеств решений неравенств разного вида (приложение «Таблица»).

Равные множества.Множества, состоящие из одних и тех же элементов, считают равными.

Например, А = {1, 2, 3}; В ={ х ç(х - 1)(х - 2)(х - 3) = 0 }. А = В.

Отношение равенства для множеств, как и отношение равенства для чисел, обладает свойствами рефлексивности, симметричности и транзитивности.

То есть для любых множеств А и В справедливо:

· А = А (рефлексивность);

· Если А = В, то В = А (симметричность);

· Если А = В и В = С, то А = С (транзитивность).

Мощность множества.Для множества, имеющего конечное число элементов, мощностью называется количество его элементов.

А = {а; b; c; d}. Его мощность çАç= 4.

Если два множества имеют одинаковую мощность, говорят, что они равномощны.

Множество А равномощно множеству времён года.

Интересно, что сначала человек научился сравнивать множества по количеству элементов, а позднее – считать предметы. Сравнить два множества по количеству элементов можно так: каждому элементу одного множества ставить в соответствие элемент второго. Если все элементы «встанут» по парам, то множества равномощны. Если же при сопоставлении некоторые элементы одного из множеств останутся без пары, то оно содержит больше элементов.

Все конечные множества можно мысленно рассортировать, относя в один и тот же класс все множества с одинаковым количеством элементов. И каждому классу поставить в соответствие как характеристику этого множества некоторое число. Таким образом, натуральное число 1 - это общая характеристика всех множеств, имеющих один элемент, натуральное число 5 - это общая характеристика всех множеств, имеющих пять элементов.

Взаимно-однозначное соответствие можно установить и для бесконечных множеств.

Например, запишем в один ряд все натуральные числа, а в другой – все чётные, элемент под элементом.

1 2 3 4 5 6 7 8 9 10 11 12 . . .

2 4 6 8 10 12 14 16 18 20 22 24 . . .

Мы видим, что все числа первого множества имеют однозначно определённую пару во втором множестве и наоборот. То есть множество натуральных чисел имеет столько же элементов, сколько и множество натуральных чётных. То есть они равномощны.

Множества, равномощные множеству натуральных чисел N, называются счётными. Интересно, что счётным является, например, множество положительных рациональных чисел.

Мощность множества всех действительных чисел называется мощностью континуума. Мощность континуум имеют также все множества, равномощные интервалу (0,1). Таким образом, множество всех действительных чисел равномощно интервалу (0,1).

Отношение равномощности также обладает свойствами рефлексивности, симметричности и транзитивности.

То есть для любых множеств А и В справедливо:

· çАç = çАç

· Если çАç = çВç, то çВç = çАç;

· Если çАç = çВç и çВç = çСç, то çАç = çС ç.

Задание 2. Найдите мощность множеств:

Т - множество трёхзначных натуральных чисел;

К – множество граней куба;

Р – множество натуральных чисел, кратных 7.

Ответ: çТç= 900; çКç= 6; множество Р – счётное.

Упражнение 2. Приведите примеры множеств, равномощных множествам Т, К, Р из задания 2.

Ответ: например,

|T| = |L|, где L = {х ç-450 ≤ х < 450, xÎ Z};

|K| = |D|, где D – дни недели, кроме воскресенья;

|P| = |N|.

Учителю. Заострите внимание учащихся на различии понятий равенство множеств и равномощность множеств.

Задание 3. Заданы следующие множества: А – множество букв слова «КОЛЬЦО», В – множество букв слова «ЦОКОЛЬ», С - множество букв слова «УЛИЦА». Укажите равные и равномощные множества.

Решение. А = {К, О, Л, Ь, Ц}, В = {Ц, О, К, Л, Ь}, С = {У, Л, И, Ц, А}. Мощность каждого из этих множеств равна 5, значит, они равномощны.

А=В, т.к. порядок следования элементов является несущественным.

Ответ: А = В, çАç = çВç = çСç.

Подмножества.

Определение.Множество В называется подмножеством множества А (множество В включается в множество А), если каждый элемент множества В является элементом множества А. Символически это записывается так: В Í А.

Само множество А и пустое множество также являются подмножествами множества А:

А Í А; Æ Í А.

Определение. Множество В называется собственным подмножеством множества А,

если B Í A, но B ≠ A. В этом случае говорят, что множество В строго включается в множество А и записывают так: B Ì A.

Учителю. Для собственных подмножеств могут использоваться оба знака включения, то есть можно записать N Ì Z или N Í Z. В школе обычно используют знак строгого включения для обозначения зависимости между множеством и его подмножеством.

Упражнение 3. Приведите примеры подмножеств для множеств Т, К, Р из задания 2.

Ответ: Например:

Е = {х ç150 < х < 500, x Î N}; E Ì T

O – множество граней куба, имеющих указанную общую вершину; О Ì К

В = {7, 70, 700, 7000}; В Ì Р

Задание 4. Приведите примеры подмножеств для числовых промежутков:

А) [4,5; 11); Б) ( ; ); В) (-0,999; 0]; Г) ( ; ].

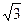Ответ: разные варианты, например ( ; ].

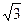Упражнение 4. Исследуйте, обладают ли отношения включения и строгого включения свойствами рефлексивности, симметричности и транзитивности.

Учителю. Разбейте учеников на несколько групп и предложите самостоятельно сделать выводы. Пусть на обсуждении каждая группа представит своё решение.

Решение. Отношение включения обладает свойством рефлексивности, а отношение строгого включения нет:А Í А; А Ë A.

Отношение включения обладает свойством симметричности в случае, если А= В, в остальных нет, а отношение строгого включения никогда не симметрично.

Транзитивностью обладают и отношения включения и строгого включения.

А Í В и В Í С, то А Í С.

А Ì В и В Ì С, то А Ì С.

Универсальное множество. Часто бывает, что все множества из какой-то группы рассматриваемых множеств являются подмножествами какого-то одного множества. Например, множество ромбов, множество трапеций, множество прямоугольников, множество квадратов являются подмножествами множества четырехугольников. Числовые множества являются подмножествами множества действительных чисел.

Такие множества, включающие в себя другие множества, называются универсальными и обозначаются обычно буквой U.Часто универсальное множество не указывается явно, но из текста бывает понятно, о каком универсальном множестве идёт речь. Например, для множеств, рассматриваемых при решении задач на делимость, универсальным будет множество целых чисел.

Задание 5.Возьмите в качестве универсального множества множество четырёхугольников.

С помощью диаграмм Эйлера-Венна изобразите внутри него следующие множества: выпуклых четырёхугольников, прямоугольников, ромбов, параллелограммов, квадратов, трапеций.

Ответ:

Пересечение и объединение множеств.

Определение.Пересечением множеств А и В называется множество А Ç В, содержащее те и только те элементы, которые входят одновременно и в множество А и в множество В.

А Ç В ={ х çхÎА и хÎ В}.

Определение.Объединением множеств А и В называется множество АÈВ, состоящее из тех и только тех элементов, которые входят хотя бы в одно из множеств А или В.

АÈВ={ х çхÎА или хÎ В}.

Например, А = {1; 3; 5; 6}; B = {2; 4; 6}.

Тогда, А Ç В = {6}; А È В = {1; 2; 3; 4; 5; 6}.

Объединение и пересечение множеств на диаграммах:

Задание 6.Покажите на диаграммах пересечение и объединение множеств А и В,

если 1) А Ì В, 2) АÇ В = Æ

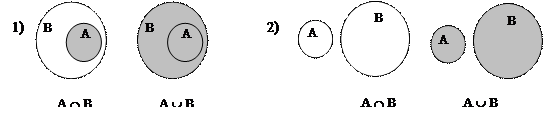Решение.

Операции пересечения и объединения множеств обладают многими свойствами, напоминающими свойства умножения и сложения действительных чисел. Перечислим основные свойства операций над множествами.

1) Коммутативность объединения и пересечения (переместительное свойство):

А È В = В È А, А Ç В = В Ç А.

2) Ассоциативность объединения и пересечения (сочетательное свойство):

(А È В) È С = А È (В È С), (А Ç В) Ç С = А Ç (В Ç С).

3) Дистрибутивность пересечения относительно объединения (распределительное свойство):

А Ç (В È С) = (А Ç В) È (А Ç С).

4) Выполняются равенства А È Æ = А, А Ç Æ = Æ, то есть роль нуля в алгебре множеств играет пустое множество.

5) Для множеств есть второй «распределительный закон», аналога которому нет для чисел. Он выражается формулой:

А È (В Ç С) = (А È В) Ç (А È С).

Упражнение 5. Сделайте иллюстрации к этим свойствам с помощью диаграмм Эйлера-Венна.

Учителю. Обратите внимание, что можно рассматривать разные варианты, которые зависят от связи множеств между собой.

Различных вариантов много, можно разбить учащихся на несколько групп и предложить

каждой группе свою картинку. Например:

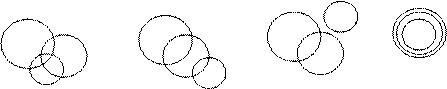
Если у вас есть возможность поработать в каком-либо графическом редакторе с показом на экране, можно провести демонстрацию, последовательно показывая результат операции над множествами.

Например: (А È В) È С = А È (В È С)

Рассмотрим некоторые свойства операций над множествами, связанные с понятием подмножества.

1) Пересечение любых множеств А и В включается в каждое из них, а каждое из этих множеств включается в их объединение:

(А Ç В) Ì А, (А Ç В) Ì В, А Ì (А È В), В Ì (А È В).

2) Для любых множеств А и В, где А есть подмножество множества В, их пересечение равно более «узкому», а объединение – более «широкому» из них:

А Ç В = А, А È В =В.

Упражнение 6. Сделайте иллюстрации к этим свойствам с помощью диаграмм Эйлера-Венна.

Рассмотрим ещё одну операцию над множествами.

Определение. Разностью множеств А и В называется множество А \ В, содержащее те и только те элементы, которые входят в множество А, но не входят в множество В.

А \ В ={ х çхÎА и х В}.

Упражнение 7. Изобразите на диаграммах все возможные варианты для множеств А и В и закрасьте разность А\ В.

Задание 7. Запишите элементы множеств А Ç В, А È В, А\ В, если:

А) А = {э, й, л, е, р}; B = {а, о, е, ё, э, и, ы, у, ю, я}.

Б) А = {3, 4, 5, 6, 7, 8}; B = {34, 56, 78}.

В) А = {7, 14, 21, 28, 35}; B = {х ç10 < х < 30, x Î N};

Г) А = {л, а, ш, м}; B = {л, м, а, ш}.

Д) А = {х ç12 ≤ х ≤ 21}; B = {х ç13 ≤ х ≤ 20}.

Ответ: А) А Ç В ={э, е}; А È В = {а, о, е, ё, э, и, ы, у, ю, я, л, р}, А\ В ={л, р};

Б) А Ç В = Æ, А È В = {3, 4, 5, 6, 7, 8, 34, 56, 78}; А\ В = {3, 4, 5, 6, 7, 8};

В) А Ç В = {14, 21, 28}; А È В = {7, 11, 12, …,28, 29, 35}; А\ В = {7, 35};

Г) А Ç В = {ш, м, л, а}, А È В = {ш, м, л, а}, А\ В = Æ, заметим, что А = В.

Д) А Ç В = {х ç13 ≤ х ≤ 20}, А È В = {х ç12 ≤ х ≤ 21}, А\ В ={х ç12 ≤ х < 13 и 20 < х ≤ 21}.

Задание 8. Приведите примеры пересечения, объединения и разности множеств для числовых промежутков.

Задание 9.

А) А = {1; 3; 5; 6}; B = {2; 4; 6}. Найдите мощность множеств А, В, А Ç В, А È В.

Б) Выведите формулы нахождения мощности пересечения и объединения множеств в различных случаях.

Ответ:А) ú Аú = 4, ú Вú = 3, ú А Ç Вú = 1, ú А È Вú = 6.

Б). Если множества не имеют общих элементов:

ú А Ç Вú = 0, ú А È Вú = ú Аú +ú Вú.

Если множество А – подмножество множества В:

ú А Ç Вú =ú Аú , ú А È Вú = ú Вú.

Если множества имеют общие элементы, но не равны:

ú А È Вú = ú Аú +ú Вú -ú А Ç Вú.

ú А Ç Вú - количество общих элементов.

Формула расчёта мощности объединения трёх множеств:

ú АÈВÈСú =ú Аú +ú Вú +ú Сú - ú АÇВú - ú АÇСú - úВÇСú +úАÇВÇСú.

Задание 10. В спортивных соревнованиях участвует школьная команда из 20 человек, каждый из которых имеет спортивный разряд по одному или нескольким из трёх видов спорта: лёгкой атлетике, плаванию и гимнастике. Известно, что 12 из них имеют спортивные разряды по лёгкой атлетике, 10 – по гимнастике и 5 – по плаванию. Сколько школьников из этой команды имеют разряды по всем видам спорта, если по лёгкой атлетике и плаванию разряды имеют 2 человека, по лёгкой атлетике и гимнастике – 4 человека, по плаванию и гимнастике – 2 человека?

Решение.Пусть А – множество учащихся, имеющих разряды по лёгкой атлетике,

В – множество учащихся, имеющих разряды по гимнастике,

С – множество школьников, имеющих разряды по плаванию. Нарисуем диаграмму.

По условию задачи имеем: ú АÈВÈСú = 20, ú Аú = 12, ú Вú = 10,

ú Сú = 5, ú АÇВú = 4, ú АÇСú = 2, ú ВÇСú = 2.

Надо найти úАÇВÇСú.

По формуле для числа элементов в объединении трёх множеств имеем:

ú АÇВÇСú = ú АÈВÈСú – ú Аú – ú Вú – ú Сú + ú АÇВú + ú АÇСú + úВÇСú =

= 20 – 12 – 10 – 5 + 4 + 2 + 2 = 28 – 27 = 1.

Таким образом, из 20 школьников, участвующих в спортивных соревнованиях, имеет разряды по всем видам спорта только один человек.

Ответ:Один человек.

Задание 11.Среди абитуриентов, поступивших в технический вуз, набрали на ЕГЭ больше 90 баллов: по математике - 48 человек, по физике – 37, по литературе – 42, по математике или физике – 75, по математике или литературе – 76, по физике или литературе – 66, по всем трём предметам – 4. Сколько абитуриентов набрали больше 90 баллов по одному предмету? Ровно по двум предметам? По меньшей мере по одному предмету?

Решение.Используем диаграммы. Через М, Ф и Л обозначим множества абитуриентов, набравших высокие баллы соответственно по математике, физике и литературе; эти множества по условию имеют соответственно 48, 37 и 42 элемента. Общая часть всех трёх множеств содержит 4 элемента. Обозначим через a, b, c, x, y, z число абитуриентов, которые набрали высокие баллы только по одному или двум из трёх предметов соответственно (см. рисунок). Пусть а – количество абитуриентов, набравших высокие баллы только по математике, b – только по физике, с – только по литературе, х – только по математике и физике, z – только по физике и литературе, у – только по математике и литературе.

С помощью рисунка условия задачи можно представить следующими уравнениями:

Получилась система шести уравнений с шестью неизвестными. Но нам нужны не неизвестные a, b, c, x, y, z, а суммы a+b+c и x+y+z. Для их нахождения сложим сначала три первых, а затем три последних уравнения системы:

Рассматривая последнюю систему уравнений как систему с двумя неизвестными, найдём из неё интересующие нас суммы: a+b+c = 65, x+y+z = 25. По меньшей мере по одному предмету набрали высокие баллы (a+b+c)+( x+y+z)+ 4 = 94.

Ответ:65, 25, 94.

Для того чтобы пользоваться теорией множеств при решении задач, встречающихся на олимпиадах, необходимо дать ученикам понимание того, что некоторые текстовые задачи имеет смысл переводить на язык множеств, пользоваться законами алгебры множеств, изображать множества с помощью диаграмм Эйлера-Венна: всё это помогает в рассуждениях при решении задач.

Задание 12.Дано: все пушистые кошки с глазами разного цвета чёрны, а все чёрные кошки с глазами разного цвета пушисты. Следует ли отсюда, что у всех пушистых чёрных кошек глаза разного цвета?

Решение. Если мы изобразим помощью кругов Эйлера множества пушистых кошек, чёрных кошек и кошек с глазами разного цвета, переводя первое и второе утверждение на язык множеств, то мы увидим, что круг, изображающий множество кошек с глазами разного цвета, находится внутри круга, изображающего чёрных пушистых кошек. То есть возможен вариант,

что у чёрных пушистых кошек глаза одинакового цвета.

Ответ: нет.

Рассмотрим уравнения с множествами. Это поможет привить некоторые навыки применения законов алгебры множеств.

Задание 13.Найдите множество Х, если Х Ç А = Х È А, где А – данное множество.

Решение.На основании свойств операций над множествами (Х Ç А) Ì Х Ì (Х È А).

Учителю. Полезно пояснять решение с помощью диаграмм для более наглядного восприятия формул.

Но так как здесь крайние множества Х Ç А и Х È А совпадают, то совпадают все три множества: Х Ç А = Х = Х È А. Когда выполняется равенство Х Ç А = Х ? Так как (ХÇА) Ì Х, то подставляя сюда вместо ХÇА множество Х, получим, что Х Ì А.

А когда выполняется равенство Х È А = Х ? Так как А Ì (Х È А), то А Ì Х.

Но включения Х Ì А и А Ì Х выполняются одновременно только тогда, когда Х = А.

Строго говоря, ещё нужно сделать проверку полученного ответа. При Х = А на основании свойств Х Ç А = А, Х È А = А, а тогда данное уравнение превращается в тождество.

Ответ:Х = А.

Задание 14.Найдите множества Х и Y из системы уравнений, где А – данное множество.

Решение.Из первого уравнения системы следует, что Х Ì А. Но тогда Х Ç А = Х, а значит, второе уравнение принимает вид Х=Y. В таком случае из первого уравнения получаем: Х=Y=A. Проверка показывает, что найденные нами значения Х=А и Y=A удовлетворяют данной системе уравнений.

Ответ:Х=Y=A.

Задание 15.Известно, что для множеств А, В и С выполняются включения

Следует ли отсюда, что А = В = С ?

Решение.Так как , то отсюда .

Так как , то .

Поскольку 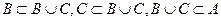, то . Из включений АÌ В и ВÌА вытекает, что А=В, а из включений С Ì А и А Ì С ,что А= С.

Значит, все три множества А, В и С равны.

Ответ:следует.

Дополнительные задачи для работы в классе – из дистанционных олимпиад прошлых лет.

Задание 16.Среди философов каждый седьмой – математик, а среди математиков каждый девятый – философ. Кого больше: математиков или философов?

А) математиков B) философов C) поровну

D) математиков в два раза больше E) определить нельзя

Решение.Пусть математиков всего было m (множество М), а философов – n (множество N). Нарисуем диаграмму для данных множеств.

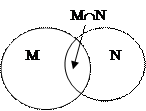m/9 – столько философов среди математиков, n/7 – математиков среди философов. Так как речь идёт о количестве элементов одного и того же множества (MÇN), то приравниваем эти количества.

m/9= n/7, то есть m = 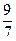n, значит математиков больше, но не в 2 раза.

Ответ: A.

Задание 17.Множество из букв какого слова не является подмножеством объединения множеств букв, из которых состоят слова «песок» и «пластичность»?

А) точность; Б) стекло; В) новость; Г) личность; Д) кость.

Ответ: В) новость.

Задание 18.В международной конференции участвуют 120 человек. Из них 60 владеют русским языком, 48 – английским, 32 – немецким, 21 – русским и английским, 19 – английским и немецким, 15 – русским и немецким, а 10 человек владеют всеми тремя языками. Сколько участников конференции не владеют ни одним из этих языков?

А) 25; B) 12; C) 18; D) 50; E) 32.

Решение.Прибавим к 60 участникам конференции, владеющим русским языком, 48 участников, владеющих английским. При этом 21 участник будет посчитан дважды, так как знает два языка и попадает в оба множества (множество участников, владеющих русским языком и множество участников владеющих английским языком), поэтому 21 человек отнимаем: 60+48 - 21=87.

Далее прибавляем 32 участника, владеющих немецким языком, при этом вычитаем 19 владеющих и немецким, и английским, и 5 (15-10), которые знают русский и немецкий, но не знают английский: 87+32 – 19 - 5=95.

95 человек знают не менее одного из трех языков (английский, немецкий, французский), остальные 25 не знают ни одного из этих языков.

Очень удобно решать эту задачу, используя диаграммы.

По условию задачи и наглядному изображению множеств легко посчитать, сколько участников знают только:

русский и английский – 11 (21-10);

английский и немецкий – 9 (19–10);

русский и немецкий – 5 (15-10);

русский – 34 (60-11-5-10);

английский - 18 (48-11-9-10);

немецкий – 8 (32-9-5-10).

По рисунку легко посчитать, что знающих хотя бы один язык – 95.

Ответ: A.

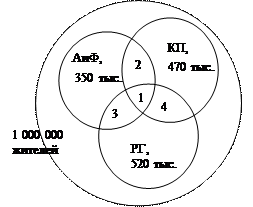
Задание 19. Из одного миллиона жителей Новосибирска 350 тысяч читают «Аргументы и факты», 520 тысяч – «Российскую газету», 470 тысяч – «Комсомольскую правду», 50 тысяч читают все три газеты, 100 тысяч - «Аргументы и факты» и «Российскую газету», 150 тысяч - «Аргументы и факты» и «Комсомольскую правду», 200 тысяч - «Комсомольскую правду» и «Российскую газету». Сколько жителей Новосибирска не читают этих газет вообще?

А) 260 тысяч В) 210 тысяч С) 160 тысяч

D) 110 тысяч E) 60 тысяч

Решение.Пересечение множеств «АиФ» и «КП» - 150 тыс., «АиФ» и «РГ» - 100 тыс., «КП» и «РГ» - 200 тыс.

Пересечение множеств «АиФ», «КП» и «РГ» - 50 тыс.

Всего читателей АиФ, КП и РГ: 350 + 520 + 470 = 1340(тыс.). Вычтем подмножества 2, 3 и 4, посчитанные дважды: 1340 – (100+150+200) = 890.

В объединение множеств подмножество 1 вошло 3 раза, но 3 раза было и вычтено.

Добавим его: 890 + 50 = 940(тыс.).

Значит, не читают этих газет: 1000 – 940 = 60 (тыс.).

Ответ:Е.