 |
|
Уравнения гидростатики
Внутри покоящейся жидкости мысленно выделим бесконечно малый прямоугольный кусочек объёмом  (рис. 1.6). Его масса
(рис. 1.6). Его масса 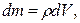 где
где  – плотность. На кусочек со стороны окружающей жидкости действуют сжимающие поверхностные силы давления, которые обозначим
– плотность. На кусочек со стороны окружающей жидкости действуют сжимающие поверхностные силы давления, которые обозначим  Пусть на него действует также массовая сила
Пусть на него действует также массовая сила 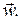 В соответствии с (1.1) общая массовая сила, действующая на массу
В соответствии с (1.1) общая массовая сила, действующая на массу  равна
равна  Так как кусочек неподвижен, сумма всех сил равна нулю:
Так как кусочек неподвижен, сумма всех сил равна нулю:
 (а)
(а)
Введём систему координат 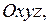 как показано на рис. 1.6. Тогда
как показано на рис. 1.6. Тогда

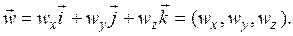
В проекциях на оси координат уравнение (а) запишется так:

Следовательно,
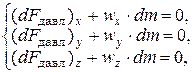 (б)
(б)
где  – координаты вектора
– координаты вектора 
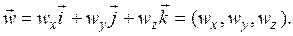
Ввиду одинаковости вида этих выражений займёмся каким-нибудь одним из них, например, вторым:
 (в)
(в)
Силы, действующие в направлении оси  давят на левую и правую грани. Обозначим
давят на левую и правую грани. Обозначим  давление жидкости на левую грань. Площадь левой грани
давление жидкости на левую грань. Площадь левой грани  поэтому на неё действует сила
поэтому на неё действует сила 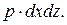 Давление на правую грань может отличаться от
Давление на правую грань может отличаться от 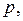 поэтому обозначим его
поэтому обозначим его  где
где  добавка к
добавка к  (частный дифференциал, или приращение давления при смещении на расстояние
(частный дифференциал, или приращение давления при смещении на расстояние  На правую грань действует сила
На правую грань действует сила  (рис. 1.6). Равенство (в) запишется так:
(рис. 1.6). Равенство (в) запишется так:


Рис. 1.6
Раскроем скобки и преобразуем левую часть. Будем иметь


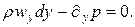 (г)
(г)
Так как добавка 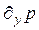 определяется по формуле
определяется по формуле
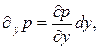
то подстановка в (г) даст
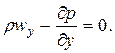
Аналогичные равенства получаются при преобразовании первого и третьего выражений в (б). В итоге получим систему дифференциальных уравнений:

|
| Уравнения гидростатики в скалярной форме |
(1.2)
Эти уравнения можно записать в компактном виде. Умножим первое уравнение на вектор 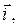 второе – на
второе – на  третье – на
третье – на  Сложим полученные равенства. Получится
Сложим полученные равенства. Получится



Раскроем скобки и перегруппируем члены

Следовательно,
 или
или

|
| Уравнения гидростатики в векторной форме |
Подробно о градиенте 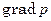 и набла-операторе
и набла-операторе  сказано в Приложении.
сказано в Приложении.
З а д а ч а 1. Найти  если
если 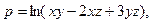

Найдём частные производные
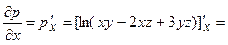
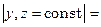
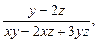
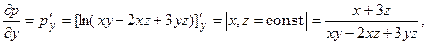
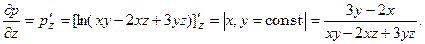
В точке М они равны:

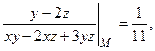


Значит, градиент в точке М равен
 <
<