Главная | Обратная связь

Оператор Гамильтона

 

Введём специальный символ

(6.1)

называемый оператором Гамильтона,или оператором набла[2].

Оператор преобразует, переводит величину в другую величину, Он обладает свойствами и вектора, и производной. Применение оператора к какой-либо величине назовём «умножением» оператора на эту величину.

1. «Умножение» на числовую функцию даст градиент этой функции:

(6.2)

¨ ■

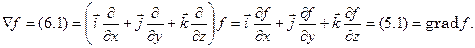2.Скалярное «умножение» на векторную функцию даст её дивергенцию:

(6.3)

¨ ■

3.Векторное «умножение» на векторную функцию даст её ротор:

 

(6.4)

 

¨ ■

 

 

Вычисление расхода через произвольную поверхность

 

Расход жидкости, или поток поля скоростей сквозь поверхность вы можете найти по формуле

в которой – уравнение поверхности, – нормальный вектор поверхности, – проекция поверхности на плоскость

Если поверхность замкнутая, то расход можно найти по формуле Остроградского-Гаусса:

где – область внутри

 

 

Циркуляция векторного поля

Вообразим, что в векторном поле имеется замкнутая линия

ЦиркуляциейЦ векторного поля по контуру называется величина

Циркуляция – это работа силы , совершаемая при движении вдоль

Пусть бесконечно малая площадка ограничена замкнутой ли­нией Циркуляцию вдоль обозначим

Величина называется плотностью циркуляции(циркуляция на единицу площади) вокруг элементарной площадки .

Формула Стокса

 

Теорема. Если поверхность натянута на контур то

(П.9.1)

¨ Мысленно разобьём на кусочки и пронумеруем их. Получим кусочки ограниченные контурами ориентированными против часовой стрелки. У каждого кусочка ( номер кусочка, ) имеется вектор площадки где – единичный вектор, нормальный к и согласованный с ориентацией контура (рис. 9.1).

Так как циркуляция аддитивна, то левая часть формулы (П.9.1) запишем так:

Правую часть формулы (П.9.1) запишем так:

Поэтому если докажем, что

(а)

то формула (П.9.1) будет доказана.

 

Рис. 9.1 Рис. 9.2

 

Построим цилиндр с основанием и высотой параллельной (рис. 9.2). Обозначим поверхность этого цилиндра. Его объём равен 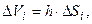поэтому Преобразуем левую часть формулы (а):

(П.1.5)

Поверхность цилиндра состоит из двух оснований и боковой поверхности. Поэтому интеграл разбивается на сумму трёх интегралов:

Следовательно,

(б)

Здесь 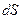– площадь элемента боковой поверхности В качестве возьмём лежащий на прямоугольник площадью (рис. 8.2), в котором – длина вектора лежащего на линии и ориентированного по этой линии. Тогда

Вектор перпендикулярен обоим векторам и (рис. 8.2), поэтому направлен вдоль единичного вектора Значит,

В итоге равенство (б) запишется так:

Получилась формула (а), и вместе с ней формула Стокса[3]. ■