Завдання до практичного заняття №2

2.1.Батарея з трьох гармат зробила залп, причому два снаряди потрапили в ціль. Знайти імовірність того, що перша гармата влучила, якщо імовірності влучення в ціль першою, другою і третьою гарматами відповідно дорівнюють 0,4; 0,3; 0,5.

2.2.Ви посадили квітку. Наскільки успішно вона зійде залежить від трьох факторів, а саме: 1) чи хороше насіння ви купили (ймовірність купити непридатне для посадки насіння – 0,3); 2) наскільки удобрену землю ви купили для посадки (рівноможливі як удобрену так і не удобрену); 3) чи не забули ви його полити (забули з вірогідністю 0,1). Отже, посаджена квітка зійде якщо насіння проклюнеться, ви купите удобрену землю і поллєте. Знайти ймовірність що квітка зійде.

2.3.ВТК перевіряє вироби на стандартність. Імовірність того, що виріб стандартний дорівнює 0,8. Знайти імовірність того, що з двох перевірених виробів обидва виявляться стандартними.

2.4.ВТК перевіряє вироби на стандартність. Імовірність того, що виріб стандартний, дорівнює 0,9. Знайти імовірність того, що з двох перевірених виробів тільки один стандартний.

2.5.Два з трьох незалежно працюючих елементів обчислювального пристрою відмовили. Знайти імовірність того, що відмовили перший і другий елементи, якщо імовірності відмовлення першого, другого і третього елементів відповідно дорівнюють 0,2; 0,3; 0,4.

2.6.Два літаки скидають по одній бомбі на військовий об’єкт. Імовірність ураження цілі першою бомбою – 0,5, а другою – 0,7. Знайти імовірність того, що ціль уразить тільки одна бомба.

2.7.Для повідомлення про аварію встановлено два незалежно працюючих сигналізатора-автомата. Ймовірність того, що при аварії спрацює, перший сигналізатор, дорівнює 0,95, а другий – 0,9. Знайти ймовірності того, що при аварії поступить сигнал: а) хоча б від одного сигналізатора; б) тільки від одного сигналізатора.

2.8.Екзаменаційний білет містить три питання. Імовірності того, що студент відповість на перший, на другий і на третій питання відповідно дорівнюють 0,7; 0,8; 0,8. Знайти імовірність того, що студент відповість на всі три питання.

2.9.Екзаменаційний білет містить три питання. Імовірності того, що студент на перше та друге питання відповість відповідно дорівнюють по 0,8, а на третє – 0,5. Знайти імовірність того, що студент здасть іспит, якщо для цього необхідно відповісти хоча б на два питання.

2.10.Імовірність влучення в ціль кожним із двох стрільців дорівнює 0,6. Стрільці стріляють по черзі, причому кожний повинний зробити не більше двох спроб. Перший, який поцілить одержує приз. Знайти ймовірність того, що приз одержить той, що стріляв першим.

2.11.Імовірність ліквідації заборгованості за користування електроенергією першим підприємством становить 0,6; другим – є додатним коренем рівняння 5р² – 4р = 0, а третім – 50% від суми двох перших ймовірностей. Визначити ймовірність того, що лише два підприємства ліквідують заборгованість.

2.12.Імовірність уражання цілі 1-м стрільцем при одному пострілі дорівнює – 0,8, а другим – 0,6. Знайти імовірність того, що ціль буде уражена одним стрільцем.

2.13.Інвестор вирішив внести порівну коштів у три підприємства за умов повернення йому кожним підприємством через визначений строк 150% від внесеної суми. Ймовірність банкрутства кожного з підприємств 0,2. Знайти ймовірність того, що після закінчення терміну кредитування інвестор одержить назад хоча б внесену суму.

2.14.Інженер розшукує формулу в двох довідниках. Імовірність того, що вона міститься в першому довіднику дорівнює 0,7; у другому – 0,8. Знайти імовірність того, що вона міститься тільки в одному довіднику.

2.15.По одній цілі з двох позицій пускають по одній ракеті. Імовірність ураження з першої позиції дорівнює 0,7; з другої – 0,6. Знайти імовірність того, що ціль буде уражена однією ракетою.

2.16.Покупець придбав телевізор і радіоприймач. Ймовірність того, що протягом гарантійного терміну телевізор не вийде з ладу 0,85; а приймач – 0,98. Знайти ймовірність того, що хоча б один з них витримає гарантійний термін.

2.17.Робітник обслуговує три верстати. Імовірність того, що протягом зміни зажадає його уваги перший верстат дорівнює 0,8; другий – 0,7; третій – 0,6. Знайти імовірність того, що протягом зміни зажадає його уваги тільки один верстат.

2.18.Робітник обслуговує три верстати. Імовірність того, що протягом зміни перший верстат зажадає уваги робітника дорівнює – 0,2; другий – 0,3; третій – 0,5. Знайти імовірність того, що протягом зміни тільки два верстати зажадають уваги робітника.

2.19.Студент розшукує потрібну формулу в трьох довідниках, імовірності того, що формула міститься в 1-му, 2-му і 3-му довідниках відповідно дорівнюють 0,7; 0,8; 0,5. Яка імовірність того, що вона міститься у всіх трьох довідниках.

2.20.Три автомашини направлені на перевезення вантажу. Ймовірність справного стану першої з них складає 0,7; другої – 0,8 і третьої – 0,5. Знайти ймовірність того, що всі три автомашини знаходяться у експлуатації.

2.21.У автогосподарстві є дві автоцистерни. Ймовірність технічної справності цих машин складає, відповідно, 0,9 та 0,8. Знайти ймовірність виконання автоцистерною роботи замовнику, що зробив напередодні замовлення на автоцистерну.

2.22.У дитячій групі вихователь відлучився до телефону. Ймовірність того, що протягом цього часу п’ять граючих дітей не зажадає увага вихователя, дорівнюють 0,7; 0,8; 0,9; 0,85; 0,75. Знайти ймовірність того, що за час відсутності вихователя жодна дитина не зажадає його уваги.

2.23.У ящику лежать однотипні деталі, причому 30% пофарбовані, а інші – ні. Визначити імовірність того, що вийняті випадково дві деталі будуть одного кольору (тобто пофарбовані).

2.24.Учень 6б класу Костя Гарбузенко і його приятель, зайнявши вигідну позицію поблизу шкільних дверей, обстрілювали сніжками усіх дівчаток, що виходили звідти. Коли двері в черговий раз відкрилися, два сніжки одночасно полетіли в голову застиглого на порозі завуча – Маргарити Вікентіївни. Яка імовірність того, що ціль була уражена, якщо відомо, що Костя звичайно попадає вісім разів з 10, а його приятель тільки сім?

2.25.32 букви російського алфавіту написані на картках розрізної абетки. П’ять карток виймають навмання послідовно одну за іншою і укладають на стіл. Знайти імовірність того, що вийде слово "АУДИТ".

2.26.Відомо, що 3% випущених деталей для телевізора є бракованими, а 80% небракованих деталей – першосортними. Яка ймовірність того, що навмання взята деталь є першосортною?

2.27.Два спортсмени незалежно друг від друга виконують одне і теж завдання. Імовірність зробити помилку для першого 0,2 і другого 0,3. Знайти імовірність того, що хоча б один з них не зробить помилки.

2.28.Для деякої місцевості середнє число ясних днів у липні дорівнює 21. Знайти імовірність того, що перші три дні липня будуть ясними.

2.29.Для руйнування моста досить влучення однієї бомби. Знайти імовірність того, що міст буде зруйнований, якщо на нього скинути три бомби, імовірності влучення яких відповідно дорівнюють 0,5; 0,7; 0,8.

2.30.Є п’ять різних ключів, з яких тільки одним можна відімкнути замок дверей. Навмання вибирається ключ і робиться спроба відімкнути замок. Ключ, що не підходить більше не використовується. Знайти ймовірність того, що: а) замок буде відімкнений першим ключем; б) для відімкнення замка буде використано не більше двох ключів.

2.31.З чотирьох букв розрізної абетки складене слово “мама”. Дитина, що не вміє читати, розсипала ці букви і потім зібрала в довільному порядку. Знайти імовірність того, що в неї знову вийде слово “мама”.

2.32.Імовірність банкрутства для однієї фірми становить 0,4, а для іншої – на 25% менше. Визначити ймовірність того, що збанкрутує хоча б одна з них.

2.33.Імовірність ураження цілі дорівнює 0,4. Знайти імовірність того, що ціль буде уражена після трьох пострілів.

2.34.На стелажі бібліотеки у випадковому порядку розставлено 14 підручників. Причому 9 з них у плетінні. Бібліотекар бере випадково 4 підручники. Знайти імовірність того, що хоча б один з узятих підручників буде в плетінні.

2.35.Одна фірма може отримати запланований прибуток з ймовірністю 0,8, а для другої фірми ця ймовірність є коренем рівняння 5р² + 2р – 3 = 0. Визначити ймовірність того, що прибуток отримає принаймні одна фірма.

2.36.Підприємство виготовляє 95% виробів стандартних, причому з них 86% – першого сорту. Знайти ймовірність того, що узятий наугад виріб, виготовлений на цьому підприємстві, виявиться першого сорту.

2.37.Студент знає 20 з 25 питань програми. Залік зданий, якщо студент відповість не менше ніж на три з чотирьох питань у білеті. Поглянувши на перше питання, студент виявив, що знає його. Яка ймовірність, що студент здасть залік?

2.38.Студент повинен скласти іспит з вищої математики. До іспиту студент допускається, якщо здані два модульних контролі. Імовірності здати перший та другий контроль для студента дорівнює 0,7 та 0,6 відповідно. При цьому студент може виконати індивідуальне завдання і захистити його з ймовірністю 0,8. В даному випадку він отримує позитивну оцінку із іспиту автоматом. Якщо індивідуальне завдання не виконується, студент може допускається до іспиту і може його скласти з ймовірністю 0,9. Яка ймовірність, що студент отримає позитивну оцінку з вищої математики?

2.39.Студент філфаку Петро уклав парі з приятелем, що, вивчивши 12 білетів з 30, він здасть залік принаймні з другого разу. Чи стоїть його приятелю битися об заклад? (Указівка: знайти відношення ймовірностей сприятливого і несприятливого для Петра подій.)

2.40.Студентка Люся до заліку устигла вивчити тільки 10 питань з 20, але сподівається, що у випадку невдачі умовить професора Аркадія Аристарховича задати їй друге питання. За багаторічними спостереженнями професора можна розжалити у двох випадках із трьох, і це співвідношення не міняється з роками. Які шанси у Люсі здати залік?

2.41.Студентка Люся знає до заліку тільки 15 питань з 30. Вона вважає, що якщо піде відповідати друга, то її шанси витягнути щасливий білет збільшаться. Чи права вона? Доведіть.

2.42.Три підприємства заключають договір про постачання певної продукції. Ймовірність виконання договору першим підприємство становить 0,9; другим – на 20% менше, а третім – 50% від суми двох перших ймовірностей. Визначити ймовірність того, що договір виконає хоча б одне підприємство.

2.43.Три підручники з економічної теорії та два з менеджменту довільно розміщено на книжковій полиці. Яка ймовірність того, що всі підручники з одного предмета виявляться поруч?

2.44.Троє незалежно вимірюють величину. Імовірність помилки першого дорівнює 0,1. Для другого і третього ця імовірність відповідно дорівнює 0,15 і 0,2. Знайти імовірність того, що при однократному вимірі хоча б один з дослідників припуститься помилки.

2.45.У деякій корпорації протокол прийняття найважливіших рішень передбачає таку процедуру. Пропозиція прямує у відділ реєстрації. У разі схвалення пропозиція прямує у відділи узгодження і контролю, а також до віце-президента Петрову. У разі схвалення віце-президентом пропозиція прямує президенту корпорації Іванову. Сюди пропозиція потрапляє і в тому випадку, якщо після його схвалення хоча б одним з відділів перевірки або контролю його схвалить віце-президент Шматко. Намалювати схему ухвалення рішення. Вважаючи, що всі інстанції ухвалюють рішення незалежно одна від одної, і що відділ реєстрації, віце-президент Петров і віце-президент Шматко схвалять пропозицію з ймовірністю 0,6, а відділи узгодження і контролю і президент Іванов – з ймовірністю 0,5, визначити ймовірність ухвалення пропозиції адміністрацією.

2.46.Числа 1,2,3,4,5 написані на п’ятьох картках. Випадково послідовно одну за іншою виймають три картки і вийняті в такий спосіб цифри ставлять зліва направо. Знайти імовірність того, що отримане тризначне число виявиться парним.

2.47.Числа 1,2,4,5,6 написані на п’ятьох картках. Випадково послідовно одну за однією виймають три картки і вийняті в такий спосіб цифри ставлять зліва направо. Знайти імовірність того, що отримане тризначне число виявиться непарним.

2.48.Яка ймовірність того, що при випадковому розміщенні в ряд карток розрізної азбуки, на яких написано букви «і», «я», «д», «е», «н», «п», «с», «т», «и», дістанемо слово «СТИПЕНДІЯ».

Контрольні питання

1. Поняття сумісних подій.

2. Поняття несумісних подій.

3. Поняття залежних подій.

4. Поняття незалежних подій.

5. Теорема додавання несумісних подій.

6. Теорема множення ймовірностей незалежних подій.

7. Теорема додавання ймовірностей сумісних подій.

8. Ймовірність появи хоча б однієї події.

9. Принцип протилежності подій.

ПРАКТИЧНЕ ЗАНЯТТЯ №3
Тема: Гіпотези. Схема незалежних випробувань

6. Формула повної ймовірності. Теорема гіпотез. Формула Байєса.Література: [15], розд. ІІІ, §8-9, с. 41-44.

Розглянемо задачу. Знайти ймовірність деякої події А, що може відбутися разом з однією з подій Н₁, Н₂, …, Н_n, що утворюють повну групу подій. Будемо називати ці події гіпотезами, тоді ймовірність події А обчислюється як сума добутків ймовірності кожної гіпотези на ймовірність події за умови, що ця гіпотеза відбулася, тобто

. (3.1)

Приклад 3.1На першому заводі на кожні сто лампочок виробляється в середньому 90 стандартних, на другому – 95, на третьому – 85, а продукція їх складає відповідно: 50%, 30%, 20% усіх електроламп, що поставляються в крамниці цього району. Знайти ймовірність придбання стандартної електролампочки ?

Розв’язання. Позначимо події: А – придбана стандартна електролампочка; Н₁ – придбана електролампочка заводу №1; Н₂ – придбана електролампочка заводу №2; Н₃ – придбана електролампочка заводу №3. Отже, відповідні ймовірності гіпотез Н_і будуть P(H₁) = 0,5; P(H₂) = 0,3; P(H₃) = 0,2; імовірності придбання стандартної електролампочки для кожного заводу відповідно ; ; .

Тоді ймовірність придбання стандартної електролампочки будь-якого заводу з (3.1) .

Наслідком теореми добутку та формули повної ймовірності є теорема Байєса.

Нехай є повна група несумісних гіпотез Н₁, Н₂, …, Н_n. Імовірності цих гіпотез до випробування відомі та дорівнюють відповідно P(H₁), P(H₂), …, P(H_n). Проведено дослідження, в результаті якого спостережена поява деякої події A. Запитується, як зміняться ймовірності гіпотез у зв’язку з появою цієї події? Формула Байєса дає відповідь на це питання.

Теорема.Ймовірність гіпотези за умови, що подія А відбулася, дорівнює відношенню добутку ймовірності даної гіпотези на умовну ймовірність появи події А при даній гіпотезі до повної ймовірності появи події А, тобто

, (3.2)

де .

Рис. 1.2

Приклад 3.2Фірма має три джерела постачання комплектуючих: А, В, С. На фірму А припадає 50% загального обсягу постачань, на В – 30% і на С – 20%. З практики відомо, що 10% деталей, які поставляються фірмою А, браковані, фірмою В – 5%, фірмою С – 6%. Яка ймовірність того, що взята навмання деталь була отримана від фірми А, та яка ймовірність того, що взята навмання бракована деталь була отримана від фірми А? Може В?

Розв’язання.Оскільки 50% комплектуючих деталей постачається фірмою А, то ймовірність того, що взята навмання деталь буде від фірми А: P(A) = 0,5.

Для вирішення другого питання розглянемо дерево ймовірностей (рис. 1.2). Імовірність того, що деталь вироблена фірмою А і при цьому бракована буде 0,5 × 0,1, для фірми В ймовірність буде 0,3 × 0,05, а для фірми С – 0,2 × 0,06.

Нехай подія D – бракована деталь будь-якої фірми, тоді D = A + B + C. Імовірність цієї події

P(D) = P(A) + P(B) + P(C) = 0,05 + 0,015 + 0,012 = 0,077.

Обчислимо частку фірми A в загальній кількості бракованих деталей

Таким чином імовірність того, що обрана деталь була отримана від фірми A за умови, коли вона виявилася бракованою змінилася з 0,5 до 0,65.

7. Повторення дослідів. Формула Бернуллі. Найімовірніше число настання події.Література: [15], розд. ІІІ, §10-11, с. 44-48.

Теорема.Якщо ймовірність р настання події А в кожному випробуванні стала, то ймовірність того, що в n незалежних випробуваннях подія A настане рівно m раз, обчислюється за формулою

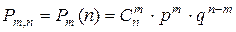, (3.3)

де q = 1 – p, .

Приклад 3.3Для нормальної роботи автобази на лінії має бути не менше восьми машин, а їх є десять. Імовірність невиходу кожної машини на лінію – 0,1. Знайти ймовірність нормальної роботи автобази в найближчий день.

Розв’язання. Позначимо події А – на лінії вісім машин; В – на лінії дев’ять машин; С – на лінії десять машин; F = A+ B+ C – нормальна робота автобази. Тоді P(F) = P(A + B + C) = P(A) + P(B) + P(C), де з (3.3) знаходимо:

; ;

; .

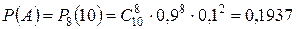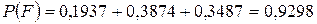Приклад 3.4 Серед вироблюваних робітником деталей у середньому 40% браку. Яка імовірність того, що серед узятих на випробування п’яти деталей, не знайдеться жодної бракованої?

Розв’язання. Позначимо A – жодної бракованої з п’яти деталей. За умовою задачі 40% браку означає, що ймовірність вироблення робітником будь-якої бракованої деталі дорівнює 0,4. Отже, можна скористатися формулою Бернуллі (3.3): .

Приклад 3.5Чінгачгук та його блідолиций брат, засівши у вежі з круговим обстрілом, відбивають напад п’яти французьких солдатів. У кожного з героїв у карабіні по п’ять куль, і поки вони можуть стріляти, підступитися до них неможливо. У французів велика кількість патронів. Крім того, у них досить зручна позиція за скелями, і імовірність потрапити в кожного з них дорівнює ½. Яка імовірність того, що французи будуть цілком розбиті?

Розв’язання. Позначимо А – французи розбиті. Розглянемо протилежну подію 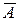– витрачено 10 куль, але принаймні один француз живий, тобто з 10 пострілів або 0 вдалих, або 1, або 2, або 3, або всього 4 вдалих. Оскільки ці події несумісні, то ймовірність суми даних подій за формулою Бернуллі (3.3) буде такою:

Þ P(A) = 1 – 386/1024 = 0,62.

Кількість настання події m₀ в n незалежних випробуваннях називається найімовірнішим, якщо ймовірність здійснення події найбільша.

При розрахунку m₀, якщо k = (n + 1) × p не ціле, існує, причому тільки одне, найімовірніше число m₀ настання події А в n незалежних випробуваннях, у кожному з яких воно може наступити з постійною ймовірністю p. Ним є найближче до числа k і менше його ціле число: m₀ = [(n + 1) × p].

Якщо ж k – ціле, тоді існує два найімовірніших числа настання події А. Ними будуть власне число k та попереднє число k – 1.

Приклад 3.6 Схожість насіння складає приблизно 80%. Знайти найімовірніше число схожого насіння серед 9.

Розв’язання. Ймовірність схожості для кожного насіння p = 0,8, тоді підрахуємо добуток (n + 1) × p, тобто k = (1 + 9) × 0,8 = 8, оскільки число вийшло ціле, існує два найімовірніших числа схожості насіння m₀ = 8або 7.

8. Локальна і інтегральна теореми Муавра-Лапласа. Формула Пуассона.Література: [15], розд. ІІІ, §12-14, с. 48-54.

Якщо число n випробувань велике для обчислення ймовірності P_m_,_n, тоді необхідно користуватися формулами Муавра-Лапласа і Пуассона.

Теорема.Якщо ймовірність p настання події A в кожному випробуванні постійна і відмінна від нуля й одиниці, а n достатньо велике, то ймовірність появи події A у n незалежних випробуваннях саме m разів за формулою Муавра-Лапласа приблизно дорівнює:

(3.4)

де ; q = 1 – p; .

Для спрощення розрахунків, пов’язаних із застосуванням формули, складена таблиця значень функції f(x) (див. Додаток А).

Користуючись цією таблицею, необхідно пам’ятати властивості функції f(x):

1) функція – парна, тобто f(–x) = f(x);

2) функція – монотонно спадаюча при додатних (від’ємних) значеннях x, тобто ;

3) якщо x > 4, то можна вважати, що f(x) » 0, тому таблицю значень f(x) наведено тільки для x Î [0; 4].

Приклад 3.7 Ймовірність народження хлопчика q = 0,515. Знайти ймовірність того, що з 200 новонароджених 95 будуть дівчата.

Розв’язання. З умови визначено n = 200, m = 95, при чому ймовірність народження дівчинки p = 1 – 0,515 = 0,485. За формулою Муавра-Лапласа (3.4) обчислимо Þ f(x) = 0,3833 Þ

Якщо ймовірність p настання події в окремому випробуванні близька до нуля, то навіть при великому числі випробувань, але при не великому розмірі добутку n×p необхідно використовувати формулу Пуассона.

Теорема.Якщо ймовірність р настання події А в кожному випробуванні стала, але мала, а число n достатньо велике, але число n×p = l невелике, то ймовірність того, що в цих випробуваннях подія A настане m раз, обчислюється за формулою

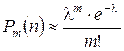. (3.5)

Для спрощення розрахунків, пов’язаних із застосуванням формули Пуассона, теж існує таблиця значень функції Пуассона (див. Додаток Б).

Приклад 3.8Ймовірність виготовлення нестандартної деталі дорівнює 0,004. Знайти ймовірність того, що серед 1000 деталей виявиться п’ять нестандартних.

Розв’язання. Оскільки ймовірність дуже мала р = 0,004, а кількість випробувань велика n = 1000, зробимо обчислення за формулою Пуассона:

l = n × p = 1000 × 0,004 = 4 Þ P₅(1000) = = 0,1563.

Зауваження. Розподіл Пуассона використовується для спрощення обчислення ймовірності при n ³ 30, p £ 0,1 та np £ 5.

Приклад 3.9 Відомо, що на 100 булочок з ізюмом трапляється одна, у якій ізюму немає взагалі. Учень 6б класу Костя Гарбузенко ставить одну жуйку Dirol проти однієї приятельської жуйки, що з купленої в шкільному буфеті булочки він виколупає хоча б чотири ізюминки. Чи справедливо таке парі? (Указівка: вважати, що число ізюминок у булочці підкоряється закону Пуассона.)

Розв’язання.Оскільки відомо, що число ізюминок в булочці підкоряється закону Пуассона (3.5), то за умовою задачі знайдемо l: P₀(100) = Þ l = ln 100. Тепер перейдемо до протилежної події і знайдемо ймовірність того, що у булочці може бути або 0, або 1, або 2, або 3 ізюминки. Тобто ймовірність цих несумісних подій за формулою Пуассона буде такою: P₀(100) +
+P₁(100)+ P₂(100) + P₃(100) = = 0,325. Звідки одержимо ймовірність, що в булочці знайдеться хоча б 4 ізюминки, тобто 1 – 0,325 = 0,675 – це означає, що парі вигідніше для Кості.

Приклад 3.10 У щоденнику учня 6б класу Кості Гарбузенка 60 сторінок і тільки одна з них без єдиного зауваження, що є чистою випадковістю. Скільки в щоденнику сторінок із трьома зауваженнями? (Указівка: знайти імовірність того, що на довільній сторінці є три зауваження, вважаючи, що число зауважень на сторінці підкоряється закону Пуассона.)

Розв’язання. Число сторінок без зауважень буде дорівнювати N₀=60 × P₀(n) = =60 × =1. Звідки знаходимо середнє число зауважень на сторінці l= 4,09. Очікуване число сторінок з трьома зауваженнями дорівнює N₀=60 × P₀(n) = 60 ´
´ = 11,4.

Часто на практиці необхідно знати ймовірність настання події не одну визначену кількість разів, а кількість разів, що знаходиться в деяких межах.В цьому випадку використовують інтегральну формулу Муавра-Лапласа.

Теорема. Якщо ймовірність р настання події А в кожному випробуванні стала і відмінна від нуля та одиниці, а кількість випробувань достатньо велика, то ймовірність того, що в n незалежних випробуваннях, подія А здійсниться кількість разів, що знаходиться в межах від a до b, обчислюється за формулою

P_n(a £ m £ b) » 0,5 × [F(x₂) – F(x₁)], (3.6)

де – називається функцією Лапласа;

; q = 1 – p.

Функція F(x) має таблицю значень, при чому для [0; 4] (див. Додаток В)і володіє такими властивостями.

1) Ф(x) – непарна ,тобто Ф(–x)= –Ф(x);

2) Ф(x) монотонно зростаюча, тобто при x₂ > x₁ Þ F(x₂) > F(x₁);

3) границя функції Ф(x) при x ® ¥ дорівнює одиниці ;

4) для всіх значень x строго більше 4 можна вважати, що F(x) » 1. Отже, таблиця Додатку В розглядає значення від 0 до 4.

Зауваження. В окремому випадку, коли границі припустимих значень числа наступу події А симетричні відносно добутку np, формула спрощується і тут використовують два наслідки інтегральної теореми Лапласа.

Наслідок 1. Якщо ймовірність р настання події А в кожному випробуванні постійна, а кількість випробувань достатньо велика, то ймовірність того, що в n незалежних випробуваннях абсолютна величина відхилення кількості настання події А від добутку np не перевищить позитивного числа r, обчислюється приблизно так:

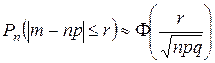. (3.7)

Наслідок 2. Ймовірність того, що в n незалежних випробуваннях абсолютне значення відхилення частоти від ймовірності події А не перевищить даного додатного числа D, приблизно дорівнює:

. (3.8)

Приклад 3.11 Електростанція обслуговує мережу з 10000 ламп, ймовірність включення кожної з них ввечері дорівнює 0,6. Визначити ймовірність того, що кількість водночас включених ламп буде між 5900 і 6100.

Розв’язання. Скористуємось інтегральною теоремою Муавра-Лапласа, тут а = 5900; b = 6100; n = 10000; p = 0,6; q = 0,4. Знаходимо: n × p = 10 000 × 0,6 = = 6 000, . Оскільки інтервал (5900; 6100) симетричний відносно 6000, то для визначення P(5900 £ m £ 6000) скористуємось формулою (3.7) наслідку 1:

Приклад 3.12 У магазині 10000 книжок. Ймовірність продажу кожної з них протягом місяця дорівнює 0,8. Яка максимальна кількість книжок буде продана протягом місяця з ймовірністю 0,999?

Розв’язання. Нехай b – максимальне число книжок, що продані протягом місяця. За умовою задачі P(0 £ m £ b) = 0,999. З іншого боку з (3.8):

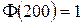, тоді .

З таблиці Додатку В знаходимо, що 0,998 = F(3,09).

Отже 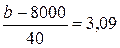, звідси b = 8124.

Таким чином, максимальне число книг, яке може бути продане протягом місяця з ймовірністю 0,999 дорівнює 8124.

Приклад 3.13 У страховій компанії 10 тис. клієнтів, що застрахували свою нерухомість. Страховий внесок складає 2 000 грош. од., ймовірність страхового випадку 0,005, страхова виплата клієнту при страховому випадку складає 200 тис. грош. од. Визначити розмір прибутку страхової компанії з ймовірністю 0,9.

Розв’язання. Прибуток компанії залежить від числа k страхових виплат при страхових випадках. Його величина дорівнює різниці між сумами страхових внесків і страхових виплат: П = 20 – 0,2k.

Наша задача складається з того, що потрібно знайти таке число N, щоб ймовірність страхового випадку P₁₀ ₀₀₀(N < k) була не більше заданої величини 1 – p, або повинна виконуватися умова: P₁₀ ₀₀₀(N < k < 10 000) £ 1 – p.

Тоді з ймовірністю p прибуток компанії складе 20 – 0,2N млн. грош. од. Таким чином, за формулою (3.8) одержимо:

З Додатку В знаходимо, що 0,8 відповідає значення аргументу функції F(x): F(1,29) = 0,8. Оскільки функція F(x) є монотонна зростаючою, то нерівність між значеннями функції F(x) переходить у нерівність того ж змісту і для відповідних аргументів: 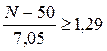. Звідки одержуємо, що N ³ 50 + 7,05 × 1,29 або N ³ 60. В цьому випадку з ймовірністю 0,9 страховій компанії гарантований прибуток П = 20 – 0,2 × 60 = 8 млн. грош. од.

Зауваження. Якщо для розглянутої прикладу 8.7 провести аналогічні обчислення визначення розміру прибутку з ймовірністю 0,995, то одержимо, що N ³ 69, а гарантований прибуток складе П = 20 – 0,2 × 69 = 6,2 млн. грош. од. Таким чином, збільшення ризику страхування може призвести до збільшення прибутку компанії. Тобто це є реалізація відомого принципу у підприємницькій діяльності: менш ризиковані, але більш надійні фінансові операції не приносять надприбутки.

⇐ Предыдущая 123 4 Следующая ⇒