 |
|
Вынужденные колебания, резонанс
Вынужденные механическиеколебания ― это колебания возникающие под действием внешней периодически изменяющейся силы. Дифференциальное уравнение, описывающее вынужденные механические колебания имеет вид:
,
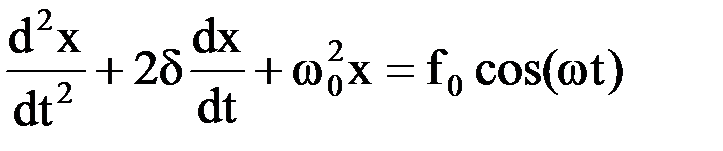где ω0 — собственная частота колебаний; δ ― коэффициент затухания; 
— внешняя периодическая сила, действующая на материальную точку и вызывающая вынужденные колебания, 
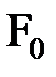― амплитудное значение этой силы; 
.
Амплитуда вынужденных механических колебаний:
.
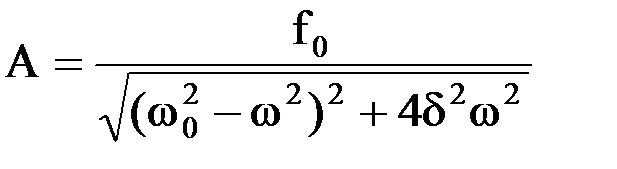Начальная фаза вынужденных механических колебаний:
.
Пример 14.13. Колебания материальной точки, происходящее под действием внешней периодически изменяющейся силы, описывается дифференциальным уравнением:
где δ – коэффициент затухания; ω0 – циклическая частота собственных колебаний; ω – циклическая частота вынужденных колебаний; f0 – амплитуда вынуждающей силы, отнесенная к массе тела. Зависимость смещения x материальной точки от времени изображена на рисунке … £ 1 R 2 £ 3 £ 4
Решение: уравнение вынужденных колебаний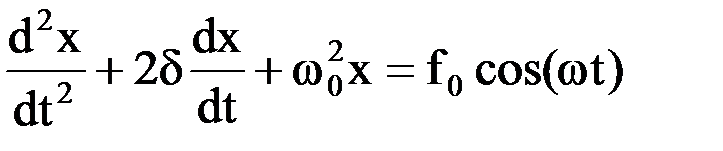 
— это линейное неоднородное дифференциальное уравнение, решение которого равно сумме общего решения однородного уравнения 
и частного решения неоднородного уравнения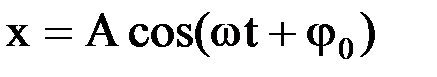 
. Общее решение играет существенную роль только в начальной стадии процесса установления гармонических колебаний с частотой ω вынуждающей силы. Из графика видно, что амплитуда вынужденных колебаний постепенно нарастает, и затем устанавливается гармоническое колебание с частотой вынуждающей силы.
Механический резонанс ―это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте равной или близкой собственной частоте колебательной системы.
Резонансная частота и резонансная амплитуда
и 
.
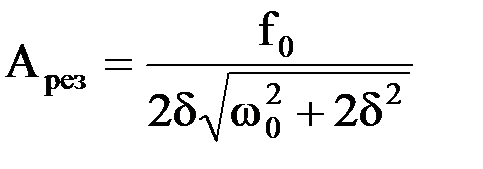Пример 14.14. Пруженный маятник с жесткостью пружины 
совершает вынужденные колебания со слабым коэффициентом затухания (δ«ω0), которые подчиняются дифференциальному уравнению 
. Амплитуда колебаний будет максимальна. Если массу груза увеличить в _______ раз(-а).
£ 3 R 9 £ 0,3 £ 0,9
Решение: явление резонанса наблюдается, когда частота вынуждающей силы равна или близка собственной частоте колебательной системы. По условию задания частота вынуждающей силы ω = 10 с-1. Известно, что для пружинного маятника 
. Из уравнения видно, что 
. Тогда реальная масса пружинного маятника 
. Условия резонанса: 
будут выполнены, если масса пружинного маятника составит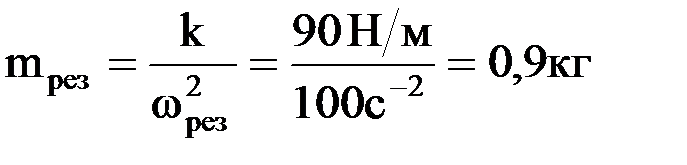 
. Следовательно, амплитуда колебаний будет максимальна (явление резонанса), если масса груза увеличить в 
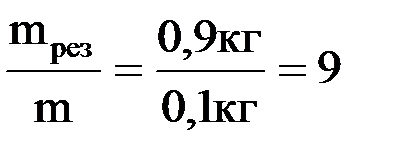раз. 
Вынужденные электромагнитные колебания ― колебания, возникающие под действием внешней, периодически изменяющейся по гармоническому закону, э.д.с.: 
Дифференциальное уравнение, описывающее вынужденные электромагнитные колебания имеет вид:
,
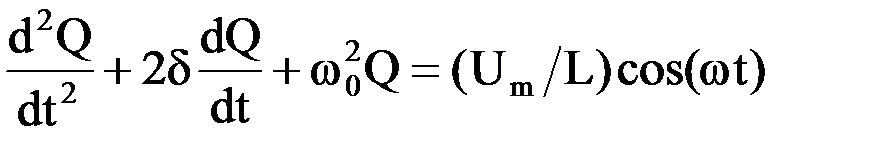где ω0 — собственная частота колебаний; δ ― коэффициент затухания; 
— внешняя периодическая сила, действующая на материальную точку и вызывающая вынужденные колебания, 
― амплитудное значение внешней, периодически изменяющейся по гармоническому закону, э.д.с.; Q — заряд конденсатора; L ― индуктивность контура.
Амплитуда вынужденных электромагнитных колебаний
.
Начальная фаза вынужденных электромагнитных колебаний
.
Пример 14.15. Вынужденные колебания заряда конденсатора в колебательном контуре описывается уравнением …
£ 
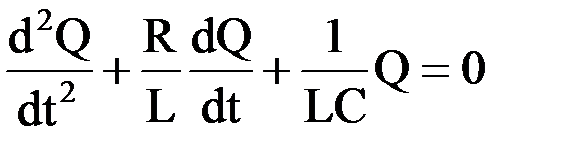
R 
£ 
Решение: дифференциальное уравнение, описывающее вынужденные электромагнитные колебания имеет вид:
,
где 
— внешняя периодическая сила, действующая на материальную точку и вызывающая вынужденные колебания, 
― амплитудное значение внешней, периодически изменяющейся по гармоническому закону, э.д.с.; Q — заряд конденсатора; L ― индуктивность контура; С — емкость конденсатора
Уравнение 
— описывает затухающие колебания контура, а уравнение 
— является дифференциальным уравнением свободных колебаний контура.
Электрический резонанс ―это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающего переменного напряжения к частоте равной или близкой собственной частоте колебательной системы.Резонансная частота и резонансная амплитуда (при малом затухании δ2«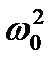 
)
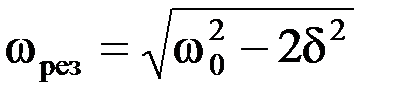и 
.
Пример 14.16. ЭДС в контуре меняется по закону: 
Зависимость силы тока от циклической частоты приведена на рисунке. Найдите значения электрического сопротивления колебательного контура во время электрического резонанса.
R 50 Ом £ 15 Ом
£ 0,2 Ом £ 2 Ом
Решение: резонансная амплитуда силы тока в колебательном контуре определяется по формуле: 
. Согласно условию задания 
. Используя график, определим 
.Тогда 
1.Уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х
или 
,
где 
— смещение точек среды с координатой х в момент времени t; A ― амплитуда; 
— фаза; 
― начальная фаза; 
— круговая частота; n=1/Т – частота; Т – период колебаний;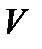 
― скорость распространения колебаний в среде (фазовая скорость); 
— волновое число 
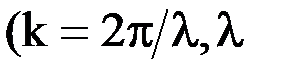― длина волны).
Пример 15.1. На рисунке представлен профиль поперечной бегущей волны, которая распространяется со скоростью 
. Амплитуда скорости колебаний точек среды (в м/с) равна …
£ 0,05 м/с R 6,28 м/с
£ 12,56 м/с £ 200 м/с
Решение:уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х: 
. В этом уравненииА — амплитуда волны, а амплитуда скорости колебаний точек среды, соответственно составит Vm = Aω. Из рисунка можно определить λ=10 м. Известно соотношение между длиной волны λ и циклической частотой: 
. Амплитуду волны определим по рисунку: А=0,05 м. Следовательно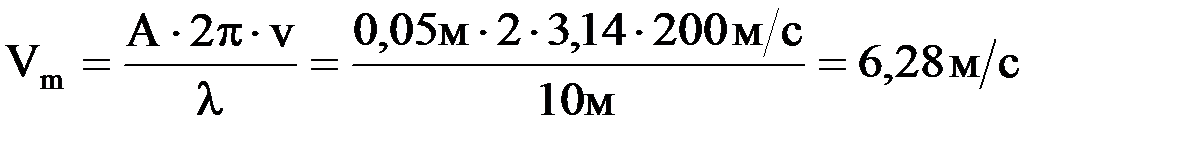 
.
Пример 15.2. На рисунке представлен профиль поперечной упругой бегущей волны. Согласно рисунку значение волнового числа равно …
£ 2,512 м-1 R 0,628 м-1£ 1,256 м-1 £ 0,314 м-1
Решение: уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х: 
. Из рисунка можно определить λ=10м. Волновое число 
.с периодом и частотой
2.Взаимосвязь длины волны, периода и частоты: 
, 
.
3. Разность фаз колебаний двух точек среды : 
,
Где Dх – расстояние между колеблющимися точками (разность хода).
4. Фазовая скорость волны:
а) продольных волн (распространяющихся в упругой среде и твердых телах): 
, гдеЕ — модуль Юнга; ρ ― плотность вещества;
б) поперечных волн:
,где G — модуль сдвига;
в) в газах: 
,где γ — показатель адиабаты (γ = ср / сv); R ― универсальная газовая постоянная; T— термодинамическая температура; μ ― молярная масса вещества.
5. Плотность энергии упругой волны: 
.
6. Средняя по времени плотность энергии волны: 
.
Пример 15.3. В упругой среде плотностью 
распространяется плоская синусоидальная волна с частотой 
и амплитудой 
. При переходе волны в другую среду, плотность которой в 2 раза меньше, амплитуду увеличивают в 4 раза, тогда объемная плотность энергии, переносимой волной, …
£ увеличится в4 раза, R увеличится в 8 раз,
£ уменьшится в 2 раза, £ не изменится.
Решение: среднее значение объемной плотности энергии равно: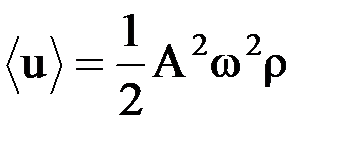 
. За счет уменьшения плотности среды объемная плотность энергии уменьшится в 2 раза, а за счет увеличения амплитуды – увеличится в 16 раз, следовательно, объемная плотность энергии увеличится в 8 раз.
7. Плотность потока энергии волны (вектор Умова)
а) мгновенное значение 
,
где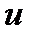 
— плотность энергии упругой волны, 
― фазовая скорость (скорость распространения волны).
б) среднее значение 
,
где 
—средняя по времени плотность энергии волны, 
― фазовая скорость.
Пример 15.4. В физиотерапии используется ультразвук частотой 800 кГц и интенсивностью 1 Вт/м2. При этом скорость ультразвуковых волн в теле человека равна 1500 м/с. При воздействии таким ультразвуком на мягкие ткани человека плотностью 1060 кг/м3 амплитуда колебаний молекул будет равна …
R 2,2 Å £ 0,22 Å £ 44 Å £ 4,4 Å
Решение: Интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова) 
, где 
—средняя по времени плотность энергии волны, A ― амплитуда; 
― фазовая скорость, 
— круговая частота; ρ ― плотность вещества (среды). Тогда из соотношения 
можно определить амплитуду 
= 2,2 Å.
Пример 15.5. Плоская электромагнитная волна распространяется в диэлектрике с проницаемостью 
. Если амплитудное значение электрического вектора волны 
, то интенсивность волны равна …( 
.)
£ 
R 
£ 
£ 
Решение: интенсивностью волны называется скалярная величина, равная модулю среднего значения вектора плотности потока энергии (вектора Умова – Пойнтинга) 
, где 
—средняя по времени плотность энергии волны, 
― фазовая скорость. Среднее значение объемной плотности энергии электромагнитной волны определяется выражением 
, а скорость волны в среде 
, где 
― абсолютный показатель преломления среды, причем 
. Для неферромагнитных сред 
. Таким образом, выражение для интенсивности электромагнитной волны можно представить в виде
8. Уравнение стоячей волны : 
.