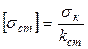Главная | Обратная связь

Поняття про стійкість форми стиснених стержнів. Критична сила.

В попередній розділах були розглянуті методи визначення напруг та деформацій при розтязі, стискові, крученні, згині та складному опорі. Міцність у всіх цих випадках визначалась величиною діючої напруги, а жорсткість-величиною деформації. При цьому малось на увазі, що дана система, деформуючись, може мати тільки одну, заздалегідь відому стійку форму рівноваги. Між іншим рівновага деформованого тіла може бути не тільки стійкою, але і не стійкою.

Для прикладу візьмемо дерев’яну лінійку для креслення і стиснемо її з двох сторін силою. При деякому значені сили лінійка залишається прямою. Збільшуючи поступово навантаження, помітимо, що в якийсь момент лінійка зігнеться. Кривизна лінійки швидко збільшується і лінійка зламається.

При цьому виявляється ,що якщо визначити напругу стиску, то вона буде в багато разів менше ніж границя міцності матеріалу з якого вона зроблена .

Звідси виходить що причиною руйнування лінійки є не порушення міцності при стискові, а втрата прямолінійної форми, тобто втрата стійкості, що викликала додаткові напруги від згину .

Із сказаного видно, що для надійної роботи конструкції крім міцності її елементів необхідно, щоб вони були стійкими .Тому стиснуті стержні, крім перевірки на міцність, перевіряють на стійкість. Вияснимо умови при яких порушується стійкість прямолінійної форми стиснутого стержня .

Нехай довгий та тонкий стержень, шарнірно закріплений на опорах, завантажений осьовою силою F, що поступово зростає (рис. 113,а) При досить малій величині сили стержень буде зберігати прямолінійну форму. Якщо такий стержень завантажити деякою поперечною силою F₁ (рис. 113,б), він зігнеться . Але якщо цю силу забрати, стержень зробить декілька коливань і знову повернеться в початкове положення. Такий стан рівноваги стиснутого стержня називається стійким.

При поступовому збільшенні сили F, ми можемо помітити що в якийсь момент стержень після зняття сили F₁ уже не повернеться в початкове положення, а залишається криволінійним, хоча до прикладання сили F₁ він був прямим. Такий прямолінійний стан рівноваги стиснутого стержня називається нестійким .

Рис.113

 

Між стійкою та нестійкою рівновагою стиснутого стержня, напевно, існує стан при якому, після зняття поперечної сили F₁,стержень може повернутись в початкове положення, а може і не повернутися. Назвемо цей стан критичним, а стискуючу силу F ,яка викликає цей стан — критичноюсилою. Тобто критична сила — це найбільша стискуюча сила, при якій ще зберігається стійка рівновага стержня, та позначається F_к .

Деформація стержня, що виражається викривленням його під дією стискуючих сил, що діють вздовж його осі, називається поздовжнім згином.

При цьому ми бачимо, що втрата стійкості відбувається в площині його найменшої жорсткості.

Теоретично дія однієї точно центральної поздовжньої стискуючої сили, що за величиною дорівнює критичній на точно вертикальний стержень із абсолютно однорідного матеріалу не повинна ні викривляти, ні руйнувати його, якщо тільки напруги в перерізі не перевищують границю текучості.

Але так як такі умови роботи стержня не реальні, навантаження, що близькі до критичної сили викликають втрату стійкості стержня. Тому в практичних розрахунках критичну силу розглядають як руйнівне навантаження.

 

§58. Формула Ейлера. Вплив кінцевих закріплень на величину критичної сили.

Встановивши поняття про критичну силу як про, "руйнівне" навантаження, що виводить стержень із стану його нормальної роботи, ми можемо скласти умову для перевірки на стійкість, аналогічну умову міцності.

Критична сила викликає в стиснутому стержні напругу, що називається "критичною напругою та позначається буквою . Критична напруга є небезпечною напругою для стиснутого стержня.

Для знаходження критичної напруги потрібно визначити критичну силу Fк, тобто найменше осьове навантаження, що здатне втримати в рівновазі трохи викривлений стиснутий стержень .

Це завдання вперше розв’язав академік Петербурзької академії наук Л. Ейлер в 1744 році.

Зазначимо, що постановка задачі інша, ніж у всіх раніш розглянутих розділах курсу. Якщо раніше ми визначали деформацію при заданих зовнішніх навантаженнях, то тут ставиться протилежне завдання: задивитись викривленням осі стиснутого стержня, потрібно визначити, при якому значенні осьової сили F таке викривлення можливе.

Розглянемо прямий стержень постійного перерізу, що шарнірно спирається своїми кінцями; одна із опор допускає можливість поздовжнього переміщення кінця стержня (рис. 114). Власною вагою стержня нехтуємо.

 

Рис114

 

Завантажимо стержень поздовжньою центрально стискуючою силою F=F_к і дамо йому досить мале викривлення в площині найменшої жорсткості; стержень утримується у викривленому стані, що можливо, так як F=F_к.

Передбачаємо, що вигин стержня досить невеликий, тому для розв’язування поставленої задачі можна скористатися наближеним диференційним рівнянням зігнутої осі стержня. Вибравши початок координат в точці А, а напрям координатних осей, як показано на рис. 114, маємо

Візьмемо переріз на відстані z від початку координат; ордината зігнутої осі в цьому перерізі буде у,а згинальний момент дорівнює .

За схемою, зображеною на рис. 114, згинальний момент виходить від’ємним, а ординати при вибраному напрямку осі у виявляються додатними. (Якби стержень вигнувся випуклістю вниз, то момент був би додатній, а у — від’ємним) .

Наведене диференційне рівняння приймає вигляд:

(135)

поділивши обидві частини рівняння на ЕІ та позначивши дріб через k², приведемо його до виду:

Загальний інтеграл цього рівняння має вигляд:

у=а sin kz + в cos kz (136)

Цей розв’язок містить в собі три невідомих: постійні інтегрування а і b, а також так як величина критичної сили нам невідома.

Умови на кінцях стержня дають два рівняння:

в точці А при z =0 прогин у = 0

в точці В при z =l прогин у = 0

Із першої умови виходить (так як sin kz=0 і cos kz=1)

0 = b.

Таким чином, зігнута вісь є синусоїдою з рівнянням

у=а sin kz. (137)

Застосувавши другу умову, підставимо в це рівняння у = 0 і z = l; маємо

0 = а sin kl (138)

Звідси виходить, що або а, або kl дорівнює нулю. Якщо а дорівнює нулю, то із рівняння (137) випливає, що прогин в любому перерізі стержня дорівнює нулю, тобто стержень залишається прямолінійним. Це суперечить вихідній передумові нашого висновку. Отже, sin kl = 0, а величина kl може мати, слідуючий нескінченний ряд значень:

kl = 0, , 2 ,3n,.....,n ;

де n- будь-яке число.

 

Звідси, , а так як , то

і (139)

Інакше кажучи, навантаження, що здатне утримати злегка викривлений стержень в рівновазі, теоретично може мати цілий ряд значень. Але так як знаходиться, та представляє інтерес з практичної точки зору, найменше значення осьової стискуючої сили, при якій стає можливим поздовжній згин, то потрібно приймати n=n_min.

Перший корінь n = 0 вимагає, щоб F_к дорівнювала нулю, що не відповідає вихідним даним задачі; тому цей корінь повинен бути відкинутим та найменшим коренем приймається значення n = 1

Тоді отримаємо:

F_к= 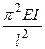(140)

(тут І — менший момент інерції поперечного перерізу стержня)

Отриманий вираз називається формулою Ейлера для стисненого стержня з шарнірно закріпленими кінцями .

Для інших способів закріплення кінців стержня формула зміниться . Випадок закріплення стиснутого стержня з шарнірно закріпленими кінцями будемо вважати першим (основним) випадком закріплення. Інші випадки закріплення будемо приводити до основного випадку. Формула Ейлера для стержня з любим закріпленням кінців має вигляд

F_к= (141)

В цій формулі коефіцієнт називається коефіцієнтом приведення довжини, який залежить від способу закріплення кінців стержня .

Всі можливі випадки закріплення кінців стержня, що зустрічається в будівельних конструкціях, можна привести до чотирьох видів (рис. 115).

 

Рис.115

 

Тобто при шарнірному закріпленні кінців (основний випадок) = 1;

при одному вільному і другому жорстко закріпленому кінцях = 2;

при одному жорстко закріпленому і другому шарнірному кінцях 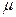≈ 0,7;

при обох жорстко закріплених кінцях = 0,5.

Величина добутку коефіцієнта приведення довжини на дійсну довжину стержня l називається приведеною, або розрахунковою довжиною стержня та позначається l_розр, тобто l_розр= l.

Таким чином, формулу (141) можна представити у вигляді

F_к= 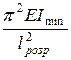(141^/)

та нею можна користуватися для визначення величини критичної сили для всіх випадків закріплення кінців стержня

Поняття про приведену довжину стержня ввів у 1892р. професор Петербурзького інституту інженерів шляхів сполучення Ф.С. Ясінський.

 

§59. Критична напруга. Гнучкість стержня. Границі застосування формули Ейлера.

Для забезпечення стійкості стержня потрібно щоб стискуюча сила F була меншого ніж критична F_к, або щоб робочі напруги в поперечних перерізах не перевищували напруг від дії критичної сили.

Напруги в поперечних перерізах стиснутого стержня від дії критичної сили F_к називаються критичними напругамита позначаються

Тобто,

Так як для стиснутого стержня критичні напруги є небезпечними, то для забезпечення стійкості прямолінійної форми стержня, потрібно до умови міцності на стиск додати ще умову стійкості

(142)

де - допустима напруга на стійкість, що дорівнює критичній напрузі, поділеній на коефіцієнт запасу стійкості k_ст, тобто

Знайдемо величину критичної напруги:

Вираз має свою, окрему назву:

- радіус інерції перерізу.

Із цього можна написати тоді

Якщо перенести величину 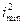в знаменник, отримаємо

(а)

Відношення розрахункової (приведеної) довжини стержня до меншого радіусу інерції називається гнучкістю стержнята позначається 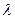, тобто

.

Підставивши значення гнучкості у формулу (а), отримаємо

(143)

Тобто, критична напруга прямо пропорційна модулю поздовжньої пружності та обернено пропорційна квадрату гнучкості стержня. Формула (143) дозволяє також встановити границі застосування формули Ейлера. Ця формула була виведена за умови, що при любому значенні F стержень працює в межах пружних деформацій. Тому її не можна застосувати у випадках, коли критичні напруги стають більшими ніж границя пропорційності.

Тому, якщо формула Ейлера справедлива,якщо то не справедлива. Очевидно, що границею застосування формули Ейлера буде випадок, коли Для практичного застосування зручно виразити границі застосування формули Ейлера через гнучкість .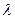

Замінимо у формулі (143) на ;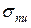

звідки визначимо граничне значення гнучкості стержня:

Прийнявши для сталі Ст.3 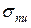=200МПа: і Е=2 , отримаємо

тобто, якщо гнучкість стержня , то формула Ейлера справедлива, якщо 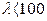, то не справедлива.

Досліди показують, що в тих випадках, коли критична напруга більша за границю пропорційності, то дійсні критичні сили виявляються набагато менші обчислених за формулою Ейлера. Ця формула, на практиці виявилась, може застосовуватись для певної категорії стержнів – тонких та довгих, тобто з великою гнучкістю, в той час як конструкції часто містять стержні з малою гнучкістю.

Тому виникла необхідність в розробці методів визначення критичних напруг і для випадків, коли вони перевищують границю пропорційності матеріалу, наприклад для будівельної сталі при гнучкості від 0 до 10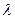0 ( =0 100). Вирішальним у цьому питанні є результати експериментальних досліджень, хоча розв’язок цієї задачі можливий і теоретичним шляхом.

Найбільш багатий дослідний матеріал був зібраний професором Ф.С. Ясінським, яким складена спеціальна таблиця критичних напруг в залежності від гнучкості для багатьох матеріалів.

На основі дослідних даних Ф.С. Ясінським була запропонована емпірична формула для визначення критичної напруги в перерізах стержнів деяких конструкційних матеріалів;

(144)

де a і b – коефіцієнт, що визначаються дослідним шляхом.

Для сталі Ст.3 формула (144) має вигляд

=338,7-1,483 ; (145)

для дерева (хвойні породи)

=29,3 – 0,194 λ МПа

Визначивши величину критичної напруги, можна знайти критичну силу за формулою

.

Формула Ф.С. Ясінського придатна не при всіх значеннях гнучкості 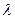. На рис.116 зображений графік залежності критичної напруги від гнучкості для сталі Ст.3. Гіпербола Ейлера, побудована за рівнянням (143) при показана пунктиром в межах =60 100, так як нею користуватися на цій ділянці не можна.

 

Рис.116

 

Для гнучкості від 0 до 60 критична напруга приблизно постійна: = або = і тому стержні розраховують не на стійкість, а на міцність. Стержні, що мають гнучкість в межах розраховується за формулою Ф.С. Ясінського.

Перейдемо тепер до питання про допустиму напругу при поздовжньому згині, яку можна визначити при великих гнучкостях ( ) по формулі (143), а при малих гнучкостях – по формулі (144), розділивши знайдені значення критичної напруги на коефіцієнт запасу стійкості k_ст.

Коефіцієнт запасу стійкості k_ст приймають в межах:

для сталі – від 1,8 до 3;

для дерева – від 2,8 до 3,2.

Отже, для кожного значення гнучкості 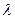можна знайти своє значення допустимої напруги при поздовжньому згині: