 |
|
Теорема Лагранжа (Жозеф Луи Лагранж, француз, 1736 – 1813 г.р.)
П. 8. Основные теоремы дифференциального исчисления
Теорема Ферма (Пьер Ферма, француз, 1601–1665 г.р.)
Пусть функция 
определена на интервале 
и в некоторой точке 
принимает наибольшее или наименьшее значение. Тогда, если в точке х0 существует конечная производная, то она равна нулю: 
Доказательство.
Пусть функция в точке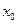 
принимает наибольшее значение, т.е. 
для любой точки 
. Это означает, что для любой точки 
справедливо неравенство 
.
Тогда, если 
, т.е. x > x0, то 
,
если 
, т.е. x < x0, то 
По условию теоремы производная в точке х0 существует. Это возможно лишь в том случае, когда справедливо равенство 
, при этом получили, что 
, 
, т.е. равенство будет справедливо лишь в одном случае, когда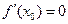 
.
(что и требовалось доказать)
Замечания.
1.Геометрический смысл теоремы: касательная к графику функции в точке M(x0,f(x0)) параллельна оси (Ох).
2. Нельзя в формулировке теоремы рассматривать не интервал , а отрезок 
.
Например, рассмотрим функцию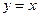 
на отрезке [0,1]. На нем функция принимает наименьшее значение y = 0 в точке х = 0, а наибольшее y = 1 в точке х = 1. Но 
и 
, так как 
для всех х.
Теорема Ролля (Ролль Мишель, француз, 1652 – 1719 г.)
Пусть на отрезке определена функция , причем
1) непрерывна на отрезке ,
2) дифференцируема на интервале ,
3) 
,
тогда существует точка 
, в которой 
Доказательство.
Пусть непрерывна на отрезке , тогда по второй теореме Вейерштрасса она достигает на этом отрезке своего максимального и минимального значений, т.е. существуют точки х1 и х2 , принадлежащие отрезку 
такие, что 
, причем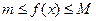 
.
Могут представиться два случая:
1) m = M, следовательно, m = M = f(x) = const = C, тогда 
в любой точке .
2) m < M, при этом , тогда хотя бы одно из двух значений m или M не принимается на концах , т.е. существует точка , в которой функция принимает либо наименьшее, либо наибольшее значение f(c). А так как функция дифференцируема на интервале , то по теореме Ферма
(что и требовалось доказать)
Замечания.
1.Геометрический смысл теоремы: у графика функции, удовлетворяющей всем трем условиям теоремы Ролля, существует точка M(с, f(с)), в которой касательная параллельна оси (Ох).
2. Все три условия теоремы существенны. Например, рассмотрим функцию 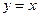на отрезке [0,1]. Данная функция непрерывна на отрезке 
, дифференцируема на интервале 
, но 
, поэтому не существует точки 
, в которой
Теорема Лагранжа (Жозеф Луи Лагранж, француз, 1736 – 1813 г.р.)
Пусть на отрезке определена функция , причем
1) непрерывна на отрезке ,
2) дифференцируема на интервале ,
тогда существует точка такая, что 
Доказательство.
Для доказательства введем в рассмотрение на следующую вспомогательную функцию:
, про которую можно сказать, что:
1) F(x) непрерывна на отрезке как разность двух непрерывных функций f(x) и 
,
2) F(x) дифференцируема на интервале : 
,
3) 
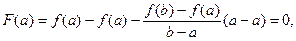
, т.е. F(a) = F(b)
Вывод: функция y = F(x) удовлетворяет всем трем условиям теоремы Ролля, следовательно, существует точка такая, что 
, т.е.
, отсюда следует утверждение теоремы, что
(что и требовалось доказать)
Замечания.
1.Величина 
угловой коэффициент секущей (М1, М2), проходящей через точки M1(a, f(a)) и M2(b, f(b)) к кривой ,
угловой коэффициент касательной l к графику функции в точке M(с, f(с)),
а так как 
, то обязательно существует точка такая, что касательная l к кривой в точке M(с, f(с)) параллельна секущей (М1, М2).
Таких точек с может быть несколько, но, по крайней мере, одна существует.
2. Равенство 
называется формулой конечных приращений Лагранжа.