Главная | Обратная связь

Общие понятия из теории устойчивости сжатых стержней

Стержни подверженные центральному сжатию при нагрузке, не превышающей некоторого опасного (критического) значения, испытывают только продольные деформации. В этом случае устойчива прямолинейная форма равновесия стержня с прямолинейной осью.

Устойчивой формой равновесия упругой системы, нагруженной внешними силами, называют такую форму равновесия, при которой, после приложения к системе некоторого малого дополнительного воздействия, система отклонится от состояния равновесия, а после снятия дополнительного воздействия возвратится к исходной форме равновесия.

Значение силы, нагрузки и напряжения, при которых первоначальная форма равновесия упругой системы становится неустойчивой, называют критической силой, критической нагрузкой и критическим напряжением.

Когда нагрузка достигнет критической величины, то стержень окажется в состоянии безразличного равновесия, прямолинейная форма равновесия становится неустойчивой, может произойти выпучивание стержня, то есть появится качественно новая, изогнутая форма равновесия стержня. При этом изгиб происходит в плоскости с меньшей изгибной жёсткостью. Появление качественно новых изгибных деформаций обусловлено дополнительными изгибающими моментами от сжимающей силы, при этом нарушается линейная зависимость между нагрузками и деформациями. Происходит существенное нарастание прогибов при небольших увеличениях сжимающей силы. Переход в критическое состояние, как правило, сопровождается потерей несущей способности стержня и называется потерей устойчивости.

Потерю устойчивости прямолинейной формы равновесия центрально сжатого стержня с прямолинейной осью называют продольным изгибом. Это одна из важнейших задач, связанных с проблемой устойчивости. Она впервые была рассмотрена Эйлером, поэтому иногда говорят «устойчивость по Эйлеру».

Для определения критической силы рассмотрим изогнутое состояние центрально сжатого стержня (рис.1).

Рис. 1. Изогнутое состояние стержня при центральном сжатии

Выпишем приближённое дифференциальное уравнение изогнутой оси стержня:

. (1)

Выражение для изгибающего момента имеет вид

. (2)

Подставив соотношение (2) в уравнение (1), получим

. (3)

Введя обозначение

, (4)

из уравнения (3) получим

. (5)

Уравнение (5) это обыкновенное дифференциальное уравнение с постоянными коэффициентами. Его решение отыскивают с помощью характеристического уравнения

.

Общее решение уравнения (5) имеет вид

, (6)

где и - произвольные постоянные интегрирования. Найдём их из условий закрепления стержня. Поскольку в начале стержня шарнирно неподвижная опора, то .

Из соотношения (6) получаем:

.

В конце стержня опора запрещает перемещение вдоль оси , следовательно, из равенства (6) получим:

.

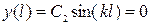Если равно нулю , то 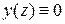и изгиба нет, что противоречит рассматриваемому изогнутому состоянию. Следовательно, равен нулю другой сомножитель .

Откуда получаем

, . (7)

Подставив в соотношение (7) выражение для параметра из равенства (4), получим выражение для критической силы:

. (8)

Для учёта других условий закрепления вводят коэффициент приведения длины 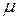и формула (8) принимает вид

. (9)

На практике из бесчисленного множества значений критических сил наиболее важна первая, наименьшая критическая сила:

. (10)

Значение коэффициента приведения длины 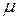для некоторых условий закрепления приведены в справочниках по сопротивлению материалов.

Критическое напряжение определяют по формуле

. (11)

Используя обозначение для квадрата радиуса инерции сечения , введя гибкость стержня

, (12)

из равенства (11) получим

,

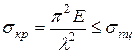поскольку при выводе пользовались приближённым дифференциальным уравнение изогнутой оси, а оно справедливо пока напряжения не превышают предел пропорциональности . Из последнего равенства находим предельное значение для гибкости стержня (границы применимости формулы Эйлера (10)):

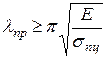. (13)

Для каждого материала предельное значение гибкости имеет своё значение. Например, для стали Ст3 это примерно 100.

Если значение гибкости , то для вычисления критического напряжения применяют эмпирическую формулу Ф. С. Ясинского:

. (14)

Для чугуна используют квадратическую зависимость:

.

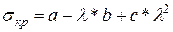Приведём значения коэффициентов для некоторых материалов (табл. 2).

Устойчивость заданного деформированного состояния конструкций обеспечивается применением нагрузок, составляющих лишь часть критических. Отношение критической нагрузки к её допускаемой величине называют коэффициентом запаса устойчивости:

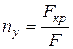. (15)

Таблица 2

Значения эмпирических коэффициентов для формулы Ясинского

 

Материал		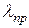a	b	c
Ст2, Ст3			1,14	-
Сталь 40			1,16
Дерево (сосна)		29,3	0,194	-
Чугун				0,053

 

 

Коэффициент определяется, в основном, в зависимости от материала стержня. Рекомендуемые величины : стальные стойки 1,5 - 3; деревянные 2,5 - 3,5; чугунные 4,5 - 5,5. Коэффициент запаса по устойчивости, как правило, выбирают большим, чем по прочности.

Условие устойчивости имеет вид

, (16)

где F - сжимающая сила; A – площадь поперечного сечения; φ - коэффициент понижения допускаемого напряжения. В левой части неравенства (16) вычисляют фактические напряжения , а в правой - допускаемые . Поскольку условие устойчивости (16) содержит два неизвестных, то расчёт выполняют итерационным методом (методом последовательных приближений).

Рассмотрим решение задачи, когда профиль сечения выбран, но неизвестна площадь поперечного сечения и известна сжимающая сила. При неизвестной силе решение задачи полностью аналогично, только из условия устойчивости находят допускаемое значение силы.