Главная | Обратная связь

Течение жидкости в трубах эллиптического и круглого сечений

Пример точного решения уравнений Навье-Стокса

 

 

Течение жидкости в трубах эллиптического и круглого сечений

 

Рассмотрим движение жидкости в цилиндрической трубе эллиптического сечения. Будем полагать режим движения жидкости ламинарным. В этом случае линии тока будут прямыми линиями, параллельными оси трубы. Подобная постановка задачи допускает точное решение уравнений Навье-Стокса, описывающих движение жидкости.

На рисунке 4.1 приведена схема течения и принятая система координат.

В силу прямолинейности линий тока только одна проекция скорости w на ось oz отлична от нуля. Поэтому система уравнений Навье-Стокса существенно упрощается и принимает вид:

; (4.1)

; (4.2)

; (4.3)

, (4.4)

где p, - соответственно плотность, давление и кинематическая вязкость.

Согласно уравнению неразрывности (4.4) компонента скорости w является функцией только координат x и y. В уравнениях движения (4.1) и (4.2) давление зависит только от координаты z. В этом случае распределение скорости в поперечных сечениях трубы одинаково, а давление изменяется только от сечения к сечению, оставаясь в данном сечении постоянным.

Решение системы (4.1) - (4.4) проведем аналогично решению, приведённому в учебнике Лойцянского Л.Г. Механика жидкости и газа. - М.: Наука, 1987. - 840с.

Учитывая (4.1), (4.2) и (4.4), уравнение (4.3) приведем к виду:

, (4.5)

где m - динамическая вязкость.

Так как = (x,y), a p = p(z), то равенство (4.5) может быть выполнено только в случае, когда

и . (4.6)

Учитывая второе равенство в (4.6), введем обозначение

, (4.7)

где - постоянное вдоль оси трубы падение давления на произвольно выбранном участке длиной = (z₂-z₁).

В расчетах перепад давления на участке трубы длиной либо задается, либо выражается через другие величины, например, расход жидкости через трубу, среднюю или максимальную скорости.

С учетом (4.7) левое уравнение в (4.6) приводится к виду:

(4.8)

где - оператор Лапласа.

Уравнение (4.8) называется уравнением Пуассона. Для его однозначного решения необходимо задать на границе сечения Г условие Дирихле:

= 0 при (x , у) Г. (4.9)

Так как сечение трубы представляет собой эллипс с полуосями а и в:

, (4.10)

то решение уравнения (4.8), удовлетворяющее граничному условию (4.9), будет иметь вид:

. (4.11)

Постоянную А в равенстве (4.11) определим после его подстановки в (4.8):

.

В результате получим распределение скорости в сечении эллиптической трубы:

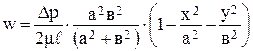. (4.12)

Из (4.12) видно, что линиями постоянной скорости, или изотахами, будут подобные друг другу эллипсы.

Максимальная скорость на оси трубы равна:

. (4.13)

Подставив (4.13) в (4.12), перепишем распределение скорости в виде:

. (4.14)

Для удобства вычисления объемного расхода жидкости Q через трубу отобразим эллипс на единичный круг с помощью формул:

x=a·x', y=в·y', r'²=x'²+y'².

Подставим эти значения в объёмный интеграл

. (4.15)

Подставив в (4.15) значение из (4.13), найдем связь между объемным расходом и падением давления вдоль трубы:

(4.16)

Учитывая, что площадь эллипса равна , определим средне-расходную скорость движения жидкости:

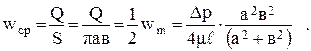(4.17)

Из полученных формул можно получить, как частный случай, основные формулы ламинарного движения вязкой несжимаемой жидкости через цилиндрическую трубу круглого сечения. Для этого, обозначив х²+у² = r², а = в = R и подставив эти выражения в (4.14), получим распределение скорости в трубе круглого сечения:

, (4.18)

где r - радиус произвольной точки;

R - радиус трубы.