 |
|
Возвратные и невозвратные состояния
Рассмотрим цепь Маркова с переходными вероятностями 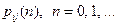 . Пусть в начальный момент система находится в некотором состоянии
. Пусть в начальный момент система находится в некотором состоянии  . Обозначим
. Обозначим  вероятность того, что система впервые вернется в исходное состояние
вероятность того, что система впервые вернется в исходное состояние  ровно через
ровно через  шагов. Тогда значение
шагов. Тогда значение
 (2.1.7)
(2.1.7)
есть вероятность того, что система на каком-либо шаге  попадает в исходное состояние
попадает в исходное состояние  , иначе
, иначе  есть вероятность возвращения в
есть вероятность возвращения в  .
.
Определение.Состояние  называется возвратным, если вероятность возвращения в него
называется возвратным, если вероятность возвращения в него
равна 1, и невозвратным, если эта вероятность меньше 1.
Теорема 1. Состояние  является возвратным тогда и только тогда, когда
является возвратным тогда и только тогда, когда
 . (2.1.8)
. (2.1.8)
Доказательство.
Имеем:  (2.1.9)
(2.1.9)
в котором положено  и дополнительно введены
и дополнительно введены  и
и  .
.
Равенство (2.1.9) является следствием общей формулы полной вероятности. Действительно, если ввести события  – “система через
– “система через  шагов впервые возвращается в исходное состояние
шагов впервые возвращается в исходное состояние  ”,
”,  , и событие
, и событие  – “система ни разу не побывает в состоянии
– “система ни разу не побывает в состоянии  в течение первых
в течение первых  шагов”, то
шагов”, то  будет полной группой событий и вероятность события
будет полной группой событий и вероятность события  – “система через n шагов будет находиться в исходном состоянии
– “система через n шагов будет находиться в исходном состоянии  ” по формуле полной вероятности есть
” по формуле полной вероятности есть
 ,
,
где  .
.
Введем аналитические при  производящие функции
производящие функции
 . (2.1.10)
. (2.1.10)
Тогда соотношение (2.1.9) можно записать в виде
 ,
,
откуда  . (2.1.11)
. (2.1.11)
Поскольку возвратность состояния  означает, что
означает, что
 ,
,
то, как видно из равенства (2.1.11), это предельное соотношение равносильно тому, что
 .
.
Но, с другой стороны,
 .
.
Следовательно, возвратность состояния  равносильна тому, что ряд
равносильна тому, что ряд  расходится. Учитывая, что
расходится. Учитывая, что  , получаем утверждение теоремы.
, получаем утверждение теоремы.
Теорема 2. Если исходное состояние  является возвратным, то система с вероятностью 1 за бесконечное число шагов бесконечно много раз возвратится в
является возвратным, то система с вероятностью 1 за бесконечное число шагов бесконечно много раз возвратится в  .
.
Если исходное состояние  является невозвратным, то за бесконечное число шагов система с вероятностью 1 лишь конечное число раз побывает в состоянии
является невозвратным, то за бесконечное число шагов система с вероятностью 1 лишь конечное число раз побывает в состоянии  .
.
Определение. Состояние  достижимо из
достижимо из  , если за некоторое число шагов система с ненулевой вероятностью переходит из
, если за некоторое число шагов система с ненулевой вероятностью переходит из  в
в  , т.е.
, т.е.  при некотором
при некотором  .
.
Определение.Если состояние  достижимо из
достижимо из  и
и  достижимо из
достижимо из  , то состояния
, то состояния  и
и  называются сообщающимися.
называются сообщающимися.
Определение.Все состояния  , достижимые из некоторого возвратного состояния
, достижимые из некоторого возвратного состояния  , образуют так называемый замкнутый класс состояний
, образуют так называемый замкнутый класс состояний  .
.
2.1.3.Эргодическая теорема о сходимости к стационарному распределению
Понятие эргодичности введено в начале 20 века в статистической физике, существенно использующей замену осреднения по статистическому ансамблю физических систем осреднением по времени вдоль траектории одной такой системы.
Определение. Распределение вероятностей
 ,
, 
называется стационарным для однородной марковской цепи  , если при начальном распределении
, если при начальном распределении  , в последующие моменты времени
, в последующие моменты времени  распределение вероятностей
распределение вероятностей
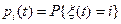 ,
, 
постоянно:  (2.1.12)
(2.1.12)
Из результата (2.1.4) следует, что распределение  является стационарным тогда и только тогда, когда оно удовлетворяет системе уравнений
является стационарным тогда и только тогда, когда оно удовлетворяет системе уравнений
 (2.1.13)
(2.1.13)
Положим, что существует хотя бы одно состояние  , в которое возможен переход из любого состояния
, в которое возможен переход из любого состояния  за время
за время  с соответствующими вероятностями
с соответствующими вероятностями
 . (2.1.14)
. (2.1.14)
Тогда можно доказать теорему о сходимости к стационарному распределению
Теорема. 1. Существует единственное стационарное распределение  , причем
, причем
 (2.1.15)
(2.1.15)
2. Для любого начального распределения  , предельные вероятности
, предельные вероятности  , одни и те же, причем оценка скорости сходимости в (2.1.15):
, одни и те же, причем оценка скорости сходимости в (2.1.15):
 . (2.1.16)
. (2.1.16)
Определение. Цепь Маркова, с не более чем счетным множеством состояний  и вероятностями перехода за
и вероятностями перехода за  шагов
шагов  , для которой существуют пределы
, для которой существуют пределы
 ,
,
не зависящие от  и образующие стационарное распределение
и образующие стационарное распределение  , называется эргодической цепью Маркова.
, называется эргодической цепью Маркова.
Случайные процессы
Определение. Случайный(стохастический) процесс  ,
,  , – это процесс, т.е. изменение во времени состояния некоторой системы, течение которого зависит от случая и для которого определена вероятность того или иного его течения.
, – это процесс, т.е. изменение во времени состояния некоторой системы, течение которого зависит от случая и для которого определена вероятность того или иного его течения.
Белый шум
Положим, что имеется семейство случайных величин 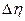 , зависящих от соответствующих конечных интервалов
, зависящих от соответствующих конечных интервалов  на конечном или бесконечном отрезке
на конечном или бесконечном отрезке  действительной
действительной
прямой так, что для любых смежных интервалов  выполняется равенство
выполняется равенство
 , (2.2.1)
, (2.2.1)
выражающее собой свойство аддитивности.
Предположим, что случайные величины  и
и  , из любых непересекающихся интервалов
, из любых непересекающихся интервалов 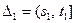 и
и  не коррелированны:
не коррелированны:
 , (2.2.2)
, (2.2.2)
и  ,
, 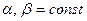 ,
,  . (2.2.3)
. (2.2.3)
Такое семейство 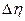 будем называть “белым шумом” и обозначать как
будем называть “белым шумом” и обозначать как 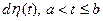 . Замечание. Процесс белого шума используется в приложениях для описания случайных возмущений с очень малым временем корреляции. Пример: “тепловой шум” – т.е. пульсации тока в проводнике, обусловленные тепловым движением электронов.
. Замечание. Процесс белого шума используется в приложениях для описания случайных возмущений с очень малым временем корреляции. Пример: “тепловой шум” – т.е. пульсации тока в проводнике, обусловленные тепловым движением электронов.
Определение. Белый шум 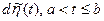 , представляющий
, представляющий  с
с  , т.е. при
, т.е. при
 , (2.2.4)
, (2.2.4)
называется стандартным белым шумом.