 |
|
Частотное представление стационарных случайных сигналов
Для канонического разложения стационарного случайного сигнала 
, заданного на интервале 
, рассмотрим его корреляционную функцию 
и разложим ее в ряд Фурье. Это разложение возможно, если считать корреляционную функцию периодически продолжающейся с периодом 
(при 
, 
, 
):
, (2.139)
где 
;
;
. (2.140)
Так как - четная функция, то выражение (2.139) можно записать в виде:
. (2.141)
Для стационарных случайных функций 
, поэтому корреляционную функцию из (2.139) можно представить в виде:
, (2.142)
что согласно (2.137) является каноническим разложением корреляционной функции, а по нему можно получить каноническое разложение центрированной случайной функции:
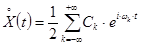, (2.143)
где 
,
а каноническое разложение стационарной случайной функции имеет вид:
. (2.144)
Исходя из выражения (2.144), при попарном объединении экспоненциальных составляющих с одинаковыми положительными и отрицательными индексами K можно привести каноническое разложение к тригонометрической форме:
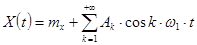, (2.145)
где ;
;
;
.
Таким образом, стационарную случайную функцию на ограниченном интервале можно представить совокупностью гармонических составляющих с амплитудами, являющимися некоррелированными случайными величинами, математические ожидания которых равны нулю. На рис.2.16 представлена спектральная диаграмма стационарной случайной функции, на которой каждой гармонике соответствует вертикальный отрезок с длиной, пропорциональной дисперсии ее амплитуды.
 |
Чтобы получить описание стационарной случайной функции на бесконечном интервале 
, необходимо перейти к интегральному каноническому разложению, которое может быть получено из выражения (2.139) путем предельного перехода при 
. При этом переходе, как видно из (2.140), происходит уменьшение значений дисперсий и сокращается расстояние между спектральными линиями, так как
.
При достаточно большом, но конечном T определим среднюю плотность распределения дисперсии по частоте:
, (2.146)
где 
- средняя плотность дисперсии на участке, прилегающем к частоте 
.
Тогда формулы (2.139) и (2.141) с учетом (2.146) можно преобразовать к виду:
, (2.147)
, (2.148)
и перейдя к пределу при , получим
, (2.149)
где 
. (2.150)
Функцию 
называют спектральной плотностью стационарного случайного процесса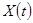 
, которая характеризует распределение дисперсии случайной функции по частотам.
Следует отметить, что величина 
является не только дисперсией 
коэффициента разложения корреляционной функции 
, но и дисперсией 
коэффициента разложения случайной функции 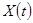, поэтому величина 
, полученная в результате предельного перехода при 
, представляет собой дисперсию, приходящуюся на спектральные составляющие стационарной случайной функции, занимающие бесконечно малый интервал частот 
.
Формулу интегрального канонического разложения корреляционной функции легко найти из формулы (2.149), подставив вместо τ его значения:
. (2.151)
Обозначив 
и повторив процедуру предельного перехода при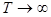 
для формулы (2.143), можно получить каноническое разложение стационарной случайной функции :
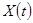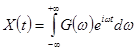, (2.152)
где функция 
есть дисперсия случайной функции 
.
Отметим основные свойства функции спектральной плотности. Для этого воспользуемся формулой Эйлера и перейдем от формулы (2.150) к одностороннему спектру в тригонометрической форме представления:
. (2.153)
Так как функция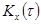 
четная, то второе слагаемое равно нулю, а первое слагаемое можно преобразовать к виду:
, (2.154)
откуда видно, что функция является действительной и четной функцией, то есть
.
Поэтому в выражении (2.149) тоже можно ограничиться только положительными частотами:
. (2.155)
Выражения (2.149) и (2.150), а также (2.154) и (2.155) являются парами интегрального преобразования Фурье (прямые и обратные). Исходя из свойств преобразования Фурье корреляционная функция 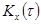и спектральная плотность подчиняются закономерности: чем уже одна из них, тем протяженнее вторая, и наоборот.
Интересно отметить, что площадь, ограниченная непрерывной кривой на спектральной диаграмме, равняется дисперсии 
случайной функции 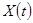. Действительно, положив в формуле (2.155) 
, получим:
. (2.156)
Если под случайной функцией 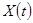подразумевать напряжение, то можно рассматривать как среднюю мощность, выделяемую этим напряжением на активном сопротивлении 1 Ом:
.
Следовательно, величина
представляет собой долю средней мощности, выделяемой составляющими спектра, относящимися к интервалу частот 
. Поэтому спектральную плотность называют еще спектральной плотностью мощности или энергетическим спектром стационарной случайной функции, поскольку имеет размерность энергии.