Главная | Обратная связь

Теорема Гаусса для электростатического поля в вакууме.

Рис.1.7. К выводу теоремы Гаусса.

Определим поток напряженности электростати­ческого поля зарядов q₁,q₂,...q_n в вакууме (e=1) через произвольную замкнутую поверхность, окружающую эти заряды.

Рассмотрим сначала случай сферической повер­х­ности радиусом R, окружающей один заряд +q, нахо­дящийся в ее центре (рис.1.7).

, где - есть интеграл по замкнутой поверхности сферы. Во всех точках сферы модуль вектора 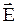одинаков, а сам он направлен перпендикулярно поверхности. Следовательно . Площадь поверхности сферы равна 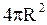. Отсюда следует, что

.

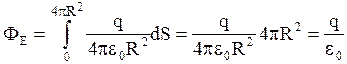Полученный результат будет справедлив и для поверхности S¢ произвольной формы, так как ее пронизывает такое же количество силовых линий.

На рисунке 1.8 представлена произвольная замкнутая поверхность, охватываю­щая заряд q>0. Некоторые линии напряженности то выходят из поверхности, то вхо­дят в нее. Для всех линий напряженности число пересечений с поверхностью являет­ся нечетным.

Как отмечалось в предыдущем параграфе, линии напря­женности, выходя­щие из объема, ограниченного замкнутой поверхностью, соз­дают положительный поток Ф_е; линии же, входящие в объем, создают отрицательный поток -Ф_е. Потоки линий при входе и выходе компенсируются. Таким образом, при расчете суммар­ного потока через всю поверхность следует учитывать лишь одно (не скомпенсированное) пересечение замкнутой поверхности каждой линией напряженности.

Если заряд q не охватывается замкнутой поверхностью S, то количество силовых линий, входящих в данную поверх­ность и выходящих из нее, одинаково (рис.1.9). Суммарный поток вектора 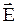через такую поверхность равен нулю: Ф_Е=0.

Рассмотрим самый общий случай поверхности про­извольной формы, охватывающей n зарядов. По принципу суперпозиции электростатических полей напряженность 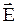, создаваемая зарядами q₁,q₂,...q_n равна векторной сумме напряженностей, создавае­мых каждым зарядом в отдельности: 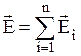. Проекция вектора 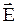- результирующей на­пряженности поля на направление нормали к пло­щадке dS равна алгебраической сумме проекций всех векторов на это направле­ние: ,

отсюда .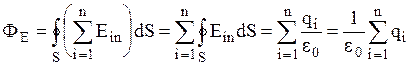

Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заря­дов, охватываемых этой поверхностью, деленной на электрическую постоян­ную e₀. Эта формулировка представляет собой теорему К.Гаусса.

В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью 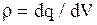, различной в разных местах пространства. Тогда суммарный заряд объема V, охватываемого замкнутой поверхностью S равен и теорему Гаусса следует записать в виде .

Теорема Гаусса представляет значительный практический интерес: с ее помо­щью можно определить напряженности полей, создаваемых заряженными телами различной формы.