Главная | Обратная связь

Числові характеристики дискретних

Випадкових величин

Закон розподілу повністю описує випадкову величину. Але часто він невідомий, і ми маємо обмаль інформації, але й така її кількість дає змогу розв’язувати багато задач. До такої інформації можна віднести числові характеристики випадкових величин. Найважливіші з них – математичне сподівання та дисперсія.

Математичним сподіванням дискретної випадкової величини називають суму добутків усіх її можливих значень і їх імовірностей, тобто

де х₁ … х_n – можливі значення дискретної випадкової величини Х,

р₁ … р_n – імовірності цих можливих значень.

Імовірнісний сенс математичного сподівання такий: математичне сподівання приблизно дорівнює (тим точніше значення, чим більша кількість випробувань) середньому арифметичному значень випадкової величини, яка спостерігається.

Властивості математичного сподівання

 

1. Математичне сподівання сталої величини дорівнює їй самій.

.

2. Сталий множник можна виносити за знак математичного сподівання, а саме:

.

3. Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань, тобто

.

4. Математичне сподівання суми двох випадкових величин дорівнює сумі математичних сподівань доданків.

.

П р и к л а д 4.6. Під час виконання трьох пострілів з рушниці ймовірність влучення у ціль кожного з них р₁= 0,4 , р₂= 0,3, р₃= 0,6. Знайти математичне сподівання загальної кількості влучень.

Р о з в ’ я з у в а н н я

Загальна кількість влучень у ціль являє собою випадкову величину Х , яку можна подати в такому вигляді: Х = Х₁ + Х₂ + Х₃, де Х₁ – випадкова величина, що означає кількість влучень у першому пострілі, Х₂ – у другому, X₃ – у третьому. Зрозуміло, що можливі значення випадкових величин Х₁, Х₂, Х₃ – це 0 і 1. А відповідні закони розподілу мають такий вигляд:

 

X1
р	0,6	0,4

 

X2
р	0,7	0,3

 

X3
р	0,4	0,6

 

Знайдемо математичні сподівання випадкових величин Х₁, Х₂, Х₃:

 

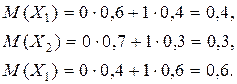
Тоді

М(Х) = М(X₁) + М(X₂) + М(X₃) = 0,4 + 0,3 + 0,6 = 1,3.

Відповідь: 1,3.

 

Розглянемо таку задачу: чому дорівнює середнє число випадків появи події А в незалежних випробуваннях, якщо ймовірність появи події А у кожному випробуванні стала й дорівнює р? Відповідь на це питання дає подана нижче теорема.

Т е о р е м а 4.1. Математичне сподівання М(Х) числа випадків появи події А під час n незалежних випробувань дорівнює добутку числа випробувань і ймовірності появи події у кожному випробуванні, а саме:

.

 

Таким чином, математичне сподівання випадкової величини, що підпорядковується біномному закону або закону Пуассона, , деn – число випробувань, р – ймовірність настання події в одному випробуванні.

Дисперсією дискретної випадкової величини називають математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання, тобто

.

 

Дисперсію також можна обчислити за такою формулою:

 

.

 

Доведіть цю формулу самостійно.

 

Властивості дисперсії

 

1. Дисперсія сталої величини дорівнює нулю, тобто

.

2. Сталий множник можна виносити за знак дисперсії , підносячи його у квадрат, а саме:

.

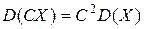3. Дисперсія суми двох незалежних випадкових величин дорівнює сумі дисперсій цих величин:

.

4. Дисперсія різниці двох незалежних випадкових величин дорівнює сумі їх дисперсій, тобто

.

 

Дисперсія характеризує відхилення випадкової величини від свого середнього значення і має розмірність, що дорівнює квадрату розмірності випадкової величини.

Для випадкової величини Х, підпорядкованої біномному закону розподілу, дисперсія 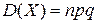, деn – число випробувань, р – ймовірність появи події під час одного випробування, а ймовірність того, що подія не відбудеться в одному випробуванні, q = 1 – p.

Ще одна важлива числова характеристика випадкової величини – середнє квадратичне відхилення.

Середнім квадратичним відхиленням (СКВ) випадкової величини Х називають таку величину:

 

Ця характеристика також описує відхилення випадкової величини від свого середнього значення, але має ту саму розмірність, що й випадкова величина.