Главная | Обратная связь

Інтегральна функція розподілу випадкової величини

 

Якщо дискретну випадкову величину можна задати переліком усіх її можливих значень, то для неперервних випадкових величин такий опис неможливий. Отже, необхідний такий спосіб задання, який можна було б застосовувати до всіх типів випадкових величин. Таким способом є функція розподілу.

Інтегральною функцією розподілу, або просто функцією розподілу випадкової величини Х називають функцію F(х), яка означає для кожного значення аргументу х імовірність того, що випадкова величина Х набуде значення менше за х , тобто

 

Отже, в геометричному тлумаченні F(x) є ймовірністю того, що випадкова величина набуде значення, зображеного на числовій осі точкою, яка лежить лівіше від аргумента х.

 

Властивості інтегральної функції

 

1. Значення інтегральної функції належить відрізку [0;1].

2. F(x) – не зменшується, тобто , якщо .

Н а с л і д о к1. Імовірність того, що випадкова величина набуде значення в інтервалі (a,b), дорівнює прирощенню інтегральної функції на цьому інтервалі, тобто

Н а с л і д о к2. Ймовірність того, що неперервна випадкова величина Х набуває певного значення x₀ дорівнює 0:

.

Н а с л і д о к3. Якщо всі можливі значення випадкової величини належать інтервалу (a,b), то коли і коли

Графічно це можна зобразити таким чином (рис. 4.2):

 

Рис. 4.2. Можливий вигляд графіка інтегральної функції розподілу, коли всі значення випадкової величини належать інтервалу (a,b)

 

П р и к л а д 4.7.Дискретна випадкова величина Х задана поданою нижче таблицею розподілу.

Х
р	0,3	0,1	0,6

Побудувати інтегральну функцію розподілу випадкової величини Х та її графік.

Р о з в ’ я з у в а н н я

Можливі значення випадкової величини Х належать відрізку [1,8], тоді:

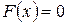1. Якщо , то (згідно з наслідком 3 другої властивості).

2. Якщо , то (згідно з наслідком 3 другої властивості).

3. Якщо , то дорівнює ймовірності події тому ;

4. Якщо , то це означає, що Х може набути таких значень та , тому за теоремою про суму незалежних подій значення функції можна обчислити таким чином:

 

Отже,

 

Графік цієї функції зображено на рис. 4.3.

 

 

Рис. 4.3. Графік інтегральної функції розподілу дискретної випадкової величини (до прикладу 4.7)

 

 

Зауважимо, що для дискретної випадкової величини графік її інтегральної функції завжди має ступінчастий вигляд.