Задачі до розділу 4

1. З партії, що налічує 50 виробів, серед яких 10 бракованих, були навмання відібрані три вироби для перевірки їхньої якості. Знайти математичне сподівання випадкової величини (ВВ) X – кількості бракованих виробів серед відібраних.

Розв’язування

Для визначення математичного сподівання необхідно скласти закон розподілу ВВ X. Можливі значення ВВ X будуть такі: 0, 1, 2, 3. Знайдемо ймовірності їх появи:

;

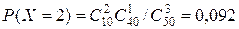Тоді закон розподілу ймовірностей ВВ X буде мати такий вигляд:

X
p	0,504	0,398	0,092	0,006

Тепер можна визначити математичне сподівання ВВ X, а саме:

Відповідь: М(Х) = 0,6.

2. Інтегральна функція розподілу ВВ X має такий вигляд:

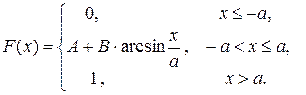
Визначити:

а) при яких значеннях і функція 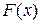є неперервною;

б) імовірність попадання ВВ X в інтервал ;

в) щільність імовірності випадкової величини X.

Розв’язування

а) Для того, щоб 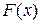була неперервною, необхідне виконання таких умов : 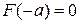, , тобто

Із цієї системи знайдемо, що ; , і ,відповідно, функція розподілу набуває такого вигляду:

б) Імовірність попадання ВВ в інтервал дорівнює різниці інтегральних функцій, аргументами яких є границі інтервалу, тобто

в) Щільність імовірності (диференціальна функція) дорівнює першій похідній від інтегральної функції розподілу, отже,

3. Випадкова величина Х задана такою функцією розподілу:

Потрібно знайти: а) щільність імовірності; б) побудувати графік функції розподілу випадкової величини Х.

Розв’язування

а) , де – щільність ймовірності, тому

б) Побудуємо графік функції розподілу випадкової величини Х (рис. 4.5).

Рис. 4.5. Графік інтегральної функції розподілу ( до задачі 3)

4. Електронний прилад складається з 1000 елементів. Імовірність відмови одного елемента протягом року роботи дорівнює 0,001 і не залежить від стану інших елементів. Яка ймовірність відмови:

а) двох елементів за рік;

б) не менше двох елементів за рік.

Розв’язування

Оскільки ймовірність появи події в одному випробуванні мала, а кількість випробувань велике, то випадкове число X елементів, що відмовили, можна вважати розподіленим відповідно до закону Пуассона, тобто

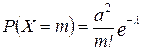тут .

а) Імовірність відмови рівно двох елементів

б) Імовірність відмови не менше двох елементів

Відповідь:а) 0,184 ; б) 0,264.

5. Вироби випробовуються із застосуванням режимів перевантаження. Імовірності того, що кожен виріб пройде випробування, дорівнюють 4/5 і не залежать одна від одної. Випробування закінчуються, як тільки один з виробів, не витримує випробування. Знайти закон розподілу ВВ Х, що являє собою число випробувань.

Відповідь:,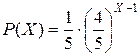

6. На шляху прямування автомашини розміщено чотири світлофори. Кожний з них або дозволяє машині їхати з імовірністю 0,6 , або забороняє – з імовірністю 0,4. Знайти закон розподілу ймовірностей ВВ Х – кількості пройдених машиною світлофорів до її першої зупинки.

Х
р	0,4	0,24	0,144	0,0864	0,1296

Відповідь:

7. Мішень має коло № 1 і два кільця із номерами 2 й 3. Влучення пострілу в коло № 1 дає 10 очок, у кільце № 2 – 5 очок, у кільце № 3 – мінус 1 очко. Імовірності влучення в коло № 1 і кільця № 2, 3 відповідно дорівнюють 0,5; 0,3; 0,2.

Знайти математичне сподівання ВВ Х – суми вибитих очок унаслідок трьох влучень у мішень.

Відповідь: 18,9.

8. Випробуваний прилад складається із трьох малонадійних елементів. Відмова кожного з них не залежить від стану іншого, а ймовірності відмови елементів з номером 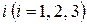. Знайти дисперсію ВВ Х, що являє собою кількість елементів, які відмовили.

Відповідь: 0,61.

9. В урну поміщено 5 білих і 3 чорних кулі. Їх виймають по одній до появи чорної кулі. Знайти математичне сподівання й дисперсію ВВ Х – кількості вийнятих білих куль, якщо кулі, які були вийняті, в урну не повертаються.

Відповідь: ; .

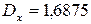10. Яким повинне бути значення параметра А, щоб функція: була диференціальною функцією розподілу ймовірностей ВВ Х, яка змінюється в нескінченних межах?

Відповідь: .

11. Інтегральна функція розподілу ймовірностей ВВ Х має такий вигляд:

Знайти диференціальну функцію та ймовірність попадання ВВ Х в інтервал (3; 6).

Відповідь: 16/25.

12. Чи може функція бути інтегральною функцією розподілу ймовірностей ВВ Х, яка змінюється в межах: а) від 0 до ; б) від 0 до ?

Відповідь: а) може; б) не може.

13. Інтегральна функція розподілу ймовірностей має такий вигляд :

Знайти диференціальну функцію та імовірність попадання ВВ Х в інтервал (5; 10) , якщо ; .

Відповідь: 0,27.

14. Побудувати інтегральну функцію розподілу дискретної випадкової величини Х, що задана зображеним нижче рядом розподілу. Знайти її математичне сподівання і дисперсію.

X_i
P_i	0,5	0,3	0,15	0,05

Відповідь: M(X) = 0,75; D(X) = 0,7875.

15. Монету підкидають 5 разів. Побудувати ряд розподілу та функцію розподілу для незалежної величини Х, яка позначає число появ герба. Знайти її математичне сподівання та дисперсію.

Відповідь: ; M(X) = 2,5; D(X) = 1,25.

16. Маємо у своєму розпорядженні три лампочки. Ймовірність того, що кожна з них має дефект, дорівнює 0,4. При вмиканні в електромережу дефектна лампа відразу перегоряє, після чого замінюється на іншу. Побудувати ряд розподілу та функцію розподілу випадкової величини Х , яка означає число лампочок, що будуть випробувані. Знайти її математичне сподівання та дисперсію.

Відповідь: M(X) = 1,56; D(X) = 0,5664.

17. Імовірність улучення в ціль при одному пострілі з рушниці дорівнює 0,4. Виконується 6 пострілів. Побудувати ряд розподілу та функцію розподілу випадкової величини Х – кількості влучень у ціль. Знайти її математичне сподівання та дисперсію.

Відповідь: ; M(X) = 2,4; D(X) = 1,44.

18. Імовірність улучення в ціль при одному пострілі з рушниці дорівнює 0,4. Виконується 5 пострілів. Побудувати ряд розподілу та функцію розподілу випадкової величини Х – кількості промахів. Знайти її математичне сподівання та дисперсію.

Відповідь: ; M(X) = 3; D(X) = 1,2.

19. Мисливець робить постріли по дичині до першого влучення, встигаючи зробити не більше трьох пострілів. Імовірність улучення в ціль при кожному пострілі дорівнює 0,8. Побудувати ряд розподілу та функцію розподілу випадкової величини Х, яка означає число пострілів, зроблених мисливцем. Знайти її математичне сподівання та дисперсію.

Відповідь: M(X) = 1,24; D(X) = 0,2624.

20. Кожен з двох стрільців робить постріл в одну мішень. Імовірність улучення в неї першим стрільцем дорівнює 0,5 другим – 0,4. Побудувати ряд розподілу та функцію розподілу випадкової величини Х , яка означає кількість влучень у мішень. Знайти її математичне сподівання та дисперсію.

Відповідь: M(X) = 0,9; D(X) = 0,89.

21. Знайти дисперсію дискретної випадкової величини Х, що означає кількість випадків появи події А в двох незалежних випробуваннях, якщо ймовірність настання події у цих випробуваннях однакова і відомо, що М(Х) = 0,9.

Відповідь: 0,495.

22. Нехай випадкова величина Y – число двійок, що випали при одному киданні трьох кубиків. Побудувати ряд розподілу випадкової величини Y. Знайти її математичне сподівання та дисперсію.

Відповідь: ; M(X) = 0,5; D(X) = 5/12.

23. Випадкова величина Х задана такою функцією розподілу:

Потрібно знайти: а) щільність імовірності; б) математичне сподівання та дисперсію; в) побудувати графіки функцій розподілу випадкової величини Х.

Відповідь: : M(X) = 3,5; D(X) = 3/4.

24. Випадкова величина Х задана такою функцією розподілу:

Відповідь: : M(X) = 4/3; D(X) = 2/9.

25. Випадкова величина Х задана диференціальною функцією розподілу:

Потрібно знайти: а) інтегральну функцію розподілу ймовірності; б) математичне сподівання та дисперсію; в) побудувати графіки функцій розподілу випадкової величини Х.

Відповідь: M(X) = 8/3; D(X) = 8/9.

26. Випадкова величина Х задана диференціальною функцією розподілу:

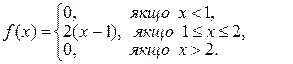
Потрібно знайти: а) інтегральну функцію розподілу ймовірності;

б) математичне сподівання та дисперсію; в) побудувати графіки функцій розподілу випадкової величини Х.

Відповідь: M(X) = 5/3; D(X) = 1/18.

27. Випадкова величина задана своєю диференціальною функцією:

Визначити параметр С та обчислити ймовірність попадання ВВ до інтервалу

Відповідь: С = –0,5;

28. Дві незалежні випадкові величини X та Y задано законами розподілу:

X							Y
p	0,5	0,2	0,1	0,2			p	0,5	0,1	0,1	0,3

Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини: Z = X + 2Y.

Розв’язування

Скористаємось властивостями математичного сподівання та дисперсії. Шукане математичне сподівання можна обчислити за формулою:

Дисперсію випадкової величини Z, враховуючи незалежність випадкових величин Х та Y, визначаємо за такою формулою:

Обчислимо та :

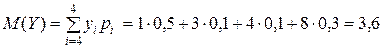тоді .

Далі обчислюємо дисперсії випадкових величин Х та Y:

;

Обчислимо тепер середнє квадратичне відхилення:

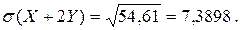
Відповідь: , ,

29. Випадкові величини Х та Y незалежні. Обчислити дисперсію дискретної випадкової величини Z = 2X + 3Y, коли відомо, що D(X) = 4, D(Y) = 5.

Відповідь: D(Z) = 61.

30. Дві незалежні випадкові величини Х та Y подані такими законами розподілу:

X							Y
p	0,1	0,3	0,4	0,2			p	0,5	0,2	0,1	0,2

Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини Z, якщо .

Відповідь: ; ; .

31. Дві незалежні випадкові величини Х та Y подані такими законами розподілу:

X							Y
p	0,1	0,3	0,4	0,2			p	0,4	0,1	0,4	0,1

Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення випадкової величини: Z = Х + 3Y.

Відповідь: ; ; .

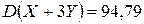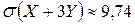32. Дві незалежні випадкові величини X та Y подані такими законами розподілу:

X							Y
p	0,1	0,2	0,2	0,5			p	0,1	0,1	0,5	0,3

Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення такої випадкової величини:

Відповідь: ; ; .

33. Дві незалежні випадкові величини X та Y подані такими законами розподілу:

X	1,5		2,5				Y
p	0,1	0,6	0,2	0,1			p	0,2	0,1	0,5	0,2

Обчислити математичне сподівання, дисперсію та середнє квадратичне відхилення такої випадкової величини:

Відповідь: ; ; .

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒