Главная | Обратная связь

Нормальний закон розподілу ймовірностей

 

Нормальний закон розподілу (часто його називають законом Гаусса) посідає дуже важливе місце в теорії ймовірності. Цей закон найчастіше спостерігається на практиці. Головна його особливість полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу, що діють в типових умовах. Ці властивості нормального закону будуть розглядатися пізніше.

Нормальним називають розподіл імовірностей неперервної випадкової величини, який описується диференціальною функцією такого вигляду:

 

.

Як бачимо, нормальний розподіл визначається двома параметрами: а та s. Імовірнісний сенс цих параметрів такий:

а – це математичне сподівання,

s – середнє квадратичне відхилення нормального розподілу.

Нормальний розподіл з будь-якими параметрами а та s називають загальним.

Нормальний закон для якого властиві такі параметри: а = 0 і s = 1, називають нормованим.

Диференціальна функція нормованого розподілу

 

.

 

Цю функцію затабульовано ( див. табл. 1 додатка 1).

З а в д а н н я.Запишіть інтегральну функцію загального та нормованого нормального закону розподілу.

Графік диференціальної функції нормального розподілу називають нормальною кривою або кривою Гаусса.

Ця крива має симетричний горбоподібний вигляд (рис. 5.2).

 

Рис. 5.2. Графік диференціальної функції нормального розподілу

 

Перелічимо властивості кривої Гаусса.

 

1. Визначена по всій числовій осі.

2. Додатна для всіх значень аргумента х.

3. Якщо х®± , то крива асимптотично наближується до осі абсцис, тобто

.

 

4. Максимального значення функція набуває, якщо х = а,воно дорівнює .

5. Графік симетричний відносно прямої: х = а.

 

З’ясуємо тепер, яким чином впливають параметри а та s на форму й розташування нормальної кривої.

Для цього розглянемо графіки диференціальних функцій нормальних законів розподілу, які мають однакові значення параметра s, але розрізняються значеннями параметра а (див. рис. 5.3).

Вочевидь, що зміна величини параметра а не змінює форми нормальної кривої, а приводить лише до її зміщення вздовж осі х таким чином: праворуч, якщо значення параметра а збільшується, і ліворуч, якщо значення а зменшується (рис. 5.3).

Рис. 5.3. Вплив параметра a на криву Гаусса, а₁ < а₂ < а₃.

 

Розглянемо тепер вплив параметра s. На рис. 5.4 зображено нормальні криві, у яких параметр а однаковий, а значення параметра σ різні. Із графіка видно, що параметр σ змінює форму кривої . При збільшенні значення σ крива буде більш пологою, тобто вона наближається до осі х, а при зменшенні σ крива буде більш “гостроверхою”, тобто, вона розтягується у додатному напрямку осі у.

Отже, можна зробити такий висновок: параметр а не змінює форми кривої Гаусса, але впливає на її розташування вздовж осі х; параметр σ не впливає на розташування кривої, але змінює її форму. При цьому для будь-яких значень параметрів а та s площа, що обмежена кривою, не змінюється і дорівнює одиниці (згідно з другою властивістю диференціальної функції).

 

 

Рис. 5.4. Вплив параметра s на криву Гаусса, σ₁< σ₂< σ₃

 

 

2.1. Імовірність попадання у даний інтервал нормально розподіленої випадкової величини

 

У багатьох задачах, пов’язаних з нормально розподіленими випадковими величинами, необхідно обчислити ймовірність того, що випадкова величина набуває значення з інтервалу від a до b.

Для обчислення цієї ймовірності скористаємось такою формулою:

,

де F(x)– функція розподілу випадкової величини Х.

Для нормального закону розподілу

 

і тому

.

 

 

Перетворимо цю формулу так, щоб можна було скористатися таблицями. Введемо нову змінну: , тоді х = sz + a, dx = sdz, і нові границі інтегрування: від до . Таким чином:

 

 

або

(5.1)

тут і являє собою функцію Лапласа, її значення протабульовані (див. табл. 2 додатка 1).

 

П р и к л а д 5.1. Випадкова величина Х розподілена за нормальним законом із такими параметрами: а = 20 і s = 5 . Знайти ймовірність того, що вона набуде значення з інтервалу (10; 30).

 

Р о з в ’ я з у в а н н я

Використаємо формулу (5.1), за умови, що a = 10, b = 30, а = 20, s = 5. Тоді

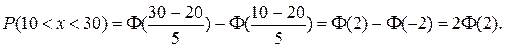
У таблиці 2 (додаток 1) знаходимо значення функції Лапласа: Ф(2) = 0,4772, і обчислюємо шукану ймовірність:

 

.

 

2.2. Обчислення ймовірності даного відхилення нормально розподіленої випадкової величини. Правило трьох сигм

У процесі розв’язування практичних задач часто виникає потреба обчислювати ймовірності того, що відхилення нормально розподіленої величини Х за абсолютним значенням менше від додатного числа d, тобто потрібно обчислити ймовірність виконання нерівності: .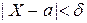

Замінимо цю нерівність рівносильною подвійною нерівністю, тобто

,

,

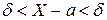і обчислимо ймовірність, використовуючи формулу попереднього параграфа, а саме:

Враховуючи непарність функції Лапласа, остаточно отримуємо, що

(5.2)

Обчислимо тепер імовірність того, що відхилення за абсолютним значенням буде меншим від потрійного середнього квадратичного відхилення. Задамо, що d = 3s, тоді

 

 

Тобто ймовірність того, що абсолютна величина відхилення буде більшою за потроєне середнє квадратичне відхилення, дуже мала, а саме: 1 – 0,9973 = 0,0027. Такі події вважають практично неможливими, у цьому й полягає сенс правила трьох сигм:

Якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання не перевищує потроєного середнього квадратичного відхилення.

2.3. Оцінка відхилення теоретичного розподілу від нормального

 

Для того, щоб кількісно оцінити відхилення теоретичного розподілу від нормального використовують такі характеристики як асиметрія та ексцес.

Асиметрією теоретичного розподілу називають відношення центрального моменту третього порядку до куба середнього квадратичного відхилення, тобто

 

.

 

Для симетричних розподілів , у тому числі й для нормального, асиметрія дорівнює 0.

Асиметрія додатна, якщо “довга частина” кривої розташована праворуч від математичного сподівання (рис. 5.5).

Рис. 5.5. Залежність асиметрії від вигляду кривої розподілу (асиметрія додатна)

 

 

Асиметрія від’ємна, якщо “довга частина” кривої розташована ліворуч від математичного сподівання ( рис. 5.6).

 

 

Рис. 5.6. Залежність асиметрії від вигляду кривої розподілу

(асиметрія від’ємна)

Ексцесом теоретичного розподілу називають таку величину:

 

Для нормального розподілу E_k = 0, коли ж E_k ¹ 0, то крива відрізняється від нормальної кривої.

Якщо ексцес додатний, то крива має більш високу та “гостру” верхівку ніж нормальна крива. Якщо ексцес від’ємний, то крива має більш низьку й плоску верхівку, ніж крива Гаусса (рис. 5.7). При цьому припускаємо, що обидві криві мають однакові математичні сподівання та дисперсії.

 

 

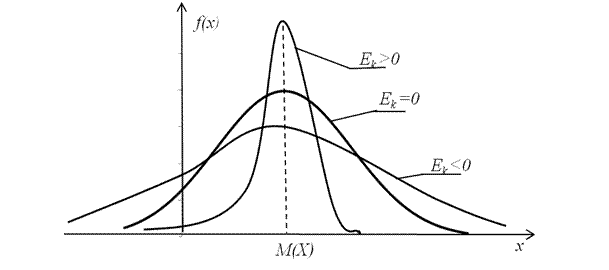
Рис. 5.7. Залежність ексцесу від вигляду кривої розподілу, нормальній кривій відповідає: E_k = 0

 

Таким чином, якщо асиметрія та ексцес даного теоретичного розподілу близькі до 0, ми можемо зробити висновок, що цей розподіл близький до нормального, і, навпаки, велике значення асиметрії та ексцесу показують суттєве відхилення розподілу від нормального.