 |
|
Закон великих чисел
Глава VIII
Теорія ймовірностей, як уже відмічалось, вивчає закономірності, які властиві масовим випадковим явищам, які відбуваються при однорідних умовах. При великому числі випробувань характеристики випадкових подій і явищ майже втрачають випадковий характер і стають закономірними. Так, наприклад, при великій кількості випробувань значення відносної частоти події набувають стійкості, так само набувають стійкості середні значення випадкових величин. Теореми, в яких з’ясовуються умови того, що сукупні дії багатьох випадкових причин приводять до результатів, які майже не залежать від випадку, отримали загальну назву закону великих чисел.
Важливе значення мають нерівності Чебешова П.Л. (1821-1894, російський математик і механік), які виражаються наступними двома теоремами.
Теорема 1.Якщо випадкова величина  має скінченне математичне сподівання
має скінченне математичне сподівання  , то для довільного
, то для довільного  справедлива нерівність
справедлива нерівність
 або
або  . (1)
. (1)
Доведення подаємо для неперервної випадкової величини. За означенням математичного сподівання

 ,
,
 де
де 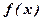 - щільність розподілу ймовірностей.
- щільність розподілу ймовірностей.
 Розіб’ємо інтервал інтегрування на дві частини тоді для довільного
Розіб’ємо інтервал інтегрування на дві частини тоді для довільного  :
:

 .
.
 (Тут враховується, що
(Тут враховується, що 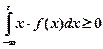 , бо за умовою
, бо за умовою  , якщо
, якщо  , то
, то 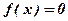 ).
).
 Отже, із нерівності
Отже, із нерівності
 .
.
 Теорема 2. Якщо випадкова величина
Теорема 2. Якщо випадкова величина  має скінченні математичні сподівання
має скінченні математичні сподівання  і дисперсію
і дисперсію  , то для довільного
, то для довільного  справедлива нерівність:
справедлива нерівність:
 або
або 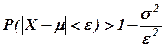 . (2)
. (2)
Доведення.Як і попередню нерівність доводимо для неперервної випадкової величини  , щільність розподілу ймовірностей якої
, щільність розподілу ймовірностей якої 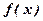 . Згідно з означенням
. Згідно з означенням
 .
.
Далі, розіб’ємо область інтегрування на три з переходом до нерівностей


 ,
,
звідси  .
.
Нерівність доведено.
Приклад 1. Середня швидкість вітру при землі в даній місцевості дорівнює 16 км/год. 1) Оцінити ймовірність того, що в цій місцевості швидкість вітру (в одному спостереженні) не перевищить 80 км/год. 2) Оцінити ту ж ймовірність, якщо відомо, що середнє квадратичне відхилення швидкості вітру дорівнює 12,8 км/год.
Розв’язання. 1) Користуючись нерівністю Чебешова (Теорема 1.), де приймаємо  ,
,  :
:
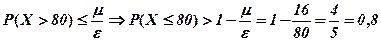 .
.
2) За другою нерівністю Чебешова (Теорема 2), в якій
 :
:
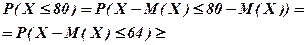
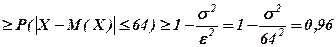 .
.
Означення.Послідовність випадкових величин  називається збіжною за ймовірністю при
називається збіжною за ймовірністю при  до випадкової величини
до випадкової величини  , (позначається
, (позначається  при
при  ), якщо для довільного, як завгодно малого
), якщо для довільного, як завгодно малого  справедлива рівність
справедлива рівність
 ,
,
або по-іншому, для довільних, як завгодно малих чисел  і
і 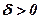 знайдеться номер
знайдеться номер 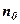 такий, що для всіх
такий, що для всіх  виконується умова
виконується умова
 .
.
Теорема 3. (Закон великих чисел у формі Чебешова).Якщо попарно незалежні випадкові величини  мають скінченні математичні сподівання
мають скінченні математичні сподівання  і дисперсії
і дисперсії  то для довільного
то для довільного  справедливе співвідношення:
справедливе співвідношення:
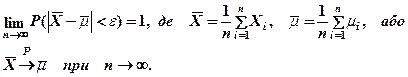 Доведення. Позначимо через
Доведення. Позначимо через  – випадкову величину
– випадкову величину
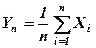 .
.
Знайдемо для  – математичне сподівання і дисперсію, користуючись відповідними властивостями (див. Гл. V, параграф 5.3.1 і 5.3.2)
– математичне сподівання і дисперсію, користуючись відповідними властивостями (див. Гл. V, параграф 5.3.1 і 5.3.2)

За другою нерівністю Чебешова (теорема 2) маємо:
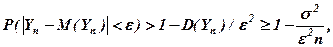 (3)
(3)
При  із нерівності (3) випливає
із нерівності (3) випливає 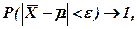 що і треба було довести.
що і треба було довести.
Наслідок. Якщо в умовах теореми величини  мають однакові значення
мають однакові значення  , то для довільного
, то для довільного  виконуються співвідношення
виконуються співвідношення

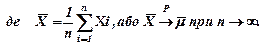
Теорема 4. (Закон великих чисел у формі Бернуллі). Нехай випадкова величина m – число “успіхів” в n незалежних випробуваннях Бернуллі. Тоді при  частота “успіхів” збігається за ймовірністю до
частота “успіхів” збігається за ймовірністю до  , де
, де  – ймовірність “успіху” при одному випробуванні, тобто
– ймовірність “успіху” при одному випробуванні, тобто

для довільного  .
.
Дійсно, нехай 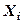 – випадкова величина задовольняє закону Бернуллі, тоді
– випадкова величина задовольняє закону Бернуллі, тоді  , а
, а  . Оскільки
. Оскільки 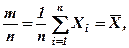 то за наслідком теореми 3 маємо для довільного
то за наслідком теореми 3 маємо для довільного 
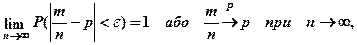
в чому і треба було переконатись.
У тих випадках, коли ряд незалежних випробувань задовольняє умовам теореми Бернуллі, нерівність Чебешова (формулу (3)) можна записати відповідно до умов теореми Бернуллі.
Нехай 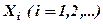 – випадкова величина, яка набуває значення 1, якщо подія А при i – тому випробуванні відбулася, і набуває значення 0, якщо подія А – не відбулася, тоді її розподіл ймовірностей
– випадкова величина, яка набуває значення 1, якщо подія А при i – тому випробуванні відбулася, і набуває значення 0, якщо подія А – не відбулася, тоді її розподіл ймовірностей

| 
| |
| P | q | p |

| 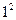
| |
| P | q | p |

| 
| 
| ||||

| 
| 
| 
| 
| 
|
Математичне сподівання і дисперсія 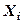 :
:
 Як і вище розглядалось, введемо випадкову величину
Як і вище розглядалось, введемо випадкову величину  її можна розглядати як відносну частоту появи однії події А в n випробуваннях, тобто
її можна розглядати як відносну частоту появи однії події А в n випробуваннях, тобто  . Тоді математичне сподівання
. Тоді математичне сподівання

дисперсія

Нерівність Чебешова (3) для теореми Бернуллі запишеться:
 (4)
(4)
Приклад 2. Для визначення середньої тривалості горіння електроламп в партії з 200 однакових ящиків було взято навмання по одній лампі з кожного ящика. Оцінити знизу ймовірність того, що середня тривалість горіння в усій партії за абсолютною величиною менше, ніж на 5 годин. Якщо відомо, що середнє квадратичне відхилення тривалості горіння електролампи для кожного з ящиків менше 7 годин.
Розв’язання. Нехай 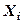 – тривалість горіння електролампи взятої з i-того ящика. Згідно з умовою задачі
– тривалість горіння електролампи взятої з i-того ящика. Згідно з умовою задачі 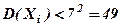 . Очевидно, що середня тривалість горіння лампи у вибірці дорівнює
. Очевидно, що середня тривалість горіння лампи у вибірці дорівнює

а середня тривалість горіння лампи у всій партії

Оцінимо ймовірність:

[За формулою, яка впливає із теореми 2 та формули (3)]
 .
.
Приклад 3. Ймовірність події А при одному випробуванні 0,8. Оцінити ймовірність того, що в 1000 незалежних випробуваннях відхилення частоти події А від ймовірності появи її в одному випробуванні за абсолютним значенням буде меншим за 0,05.
Розв’язання. За умовою задачі p=0,8; q=1-0,8=0,2; n=1000;  Розглянемо два способи розв’язання.
Розглянемо два способи розв’язання.
1-ий спосіб. За нерівністю 4 маємо:

2-ий спосіб. За формулою ймовірності відхилення відносної частоти події від її ймовірності (див. Гл. IV, §4.6)

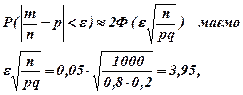
За таблицею 2 (див Додаток) Ф(3,95)  0,49995,
0,49995,

Цей результат точніший, ніж отриманий першим способом.