Главная | Обратная связь

Комбінації (сполучення)

Глава 1

Елементи комбінаторики

Розглянемо скінченну множину елементів, з яких будемо утворювати підмножини. Наприклад, множину букв, цифр, або інших об’єктів. Підмножинами можуть бути сполучення букв, цифр і ін. Так із множини цифр 0, 1, 2, ..., 9 можна утворити різні підмножини (сполучення): 123, 312, 90735, 1991, 48 і. т. д. Деякі з них, такі як 123, 312, відрізняются порядком цифр, інші, наприклад, 90735 і 48, відрізняются цифрами, а також їх кількістю.

Означення. Різні підмножини, що утворені із яких-небудь елементів і відрізняються одна від одної або самими елементами, або порядком їх розташування, називаються сполуками.

Елементи, з яких утворюються сполуки позначаються буквами .

Серед сполук розрізняють основні види: розміщення, перестановки, комбінації, а також їх види з повтореннями. Далі ми детально розглянемо кожний з цих видів сполук.

Область математики, у якій вивчається питання про кількість різних сполук, які підпорядковані тим чи іншим умовам, і які можна скласти із заданих елементів, називається комбінаторикою.

Розміщення

Нехай дано три елементи . З них можна утворити такі сполуки:

1) по одному елементу:

;

2) по два:

;

3) по три:

.

Якщо, наприклад, розглянути сполуки по два елементи, то деякі з них відрізняються елементами , інші – порядком елеметів . Такі сполуки називаються розміщеннями із 3 – х елементів по 2.

Означення 1. Розміщеннями із nелементів по m називаються такі сполуки, які містять по mелементів, взятих із даних n елементів, і які відрізняються одна від одної або елементами, або порядком елементів.

Число розміщень позначається .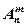

Із наведених вище прикладів ми бачимо, що , , .

Теорема.Число всіх можливих розміщень із 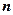елементів по 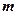дорівнює добутку 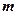послідовних натуральних чисел, з яких найбільшим є , тобто

. (1)

Дійсно, нехай нам дано 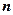елементів

.

Розглянемо розміщення по одному елементу. Зрозуміло, що їх буде 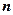, тобто

.

Тепер розглянемо, які можливі розміщення по 2 елементи. Щоб їх отримати, ми допишемо до кожного з 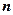даних елементів ще по одному, взятих із решти 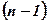елементів. Так, до елемента допишемо послідовно решту елементів: ; до елемента послідовно решту елементів і т. д. Отримаємо всі розміщення із елементів по 2:

Записано рядків 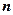, а число всіх розміщень в кожному з цих рядків 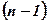. Загальна кількість всіх розміщень дорівнює добутку 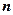на 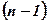, тобто

.

Щоб отримати розміщення по 3 елементи в кожному, нам потрібно до кожної із записаних пар елементів долучити ще по одному елементу із елементів, що залишились.

Наприклад, до потрібно долучити один із 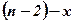елементів . Тоді всіх розміщень по 3 елементи буде:

і т. д. На 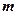-му кроці отримаємо формулу (1).

Приклад 1. Студенти групи вивчають 9 навчальних дисциплін по 3 пари щоденно. Скількома способами можна розподілити пари на день ?

Розв’язанняУсі можливі способи розподілу пар на день являють собою, очевидно, всі можливі розміщення із 9 елементів по 3, тому їх кількість дорівнює

.

У деяких задачах зустрічаються розміщення з повтореннями.

Означення 2. Розміщеннями із n елементів по m з повтореннями називаються такі сполуки, які містять по m елементів, взятих із даних n елементів, причому окремі елементи можуть появлятися раз.

Число розміщень з повтореннями позначаються через і обчислюються за формулою

. (2)

Приклад 2. Автомобільний номер складається із 5 цифр (із набору 0, 1, 2, 3, ..., 9) і 2 букв. У сполуках із букв для номерів автомобілів, які зареєстровані у Дніпропетровській області, на першому місці ставиться буква А, на другому – одна з букв А, Б, В, І, К, Н. Скільки автомобільних номерів можна скласти в області ?

Розв’язання.Числова частина номера є одним з розміщень із по 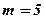з повтореннями. Їх кількість

,

із них необхідно виключити розміщення 000-00, бо такий номер не використовується, тобто всіх числових сполук буде

.

Кількість сполучень букв , а вони рахуються за другими буквами для області (перша буква – фіксована), буде шість. Загальне число всіх автомобільних номерів при згаданій системі дорівнює:

.

Перестановки

Означення. Перестановками називаються розміщення із 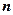елементів по 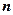і позначаються .

Згідно з означенням

.

Добуток всіх натуральних чисел від 1 до 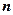позначається (читається 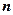факторіал).

Таким чином,

.

Тоді формула для обчислення кількості перестановок запишеться:

. (3)

При цьому мається на увазі, що .

Зауваження. Іноді зустрічається позначення . Прийнято вважати за означенням, що .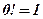

Приклад. Скільки п’ятизначних телефонних номерів, можна скласти використовуючи цифри 3, 4, 5, 6, 7 (без повторень)?

Розв’язання. Оскільки кожний номер телефона складається з п’яти цифр і за умовою використовуються тільки названі 5 цифр, то такі номери будуть відрізнятися тільки порядком цифр, тобто це будуть перестановки, і їх кількість доріврнює:

.

 

Комбінації (сполучення)

Означення. Комбінаціями (сполученнями) із 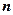елементів по 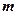(позначається ) називаються ті розміщення із 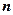елементів по 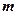, які відрізняються хоча б одним елементом.

Число комбінацій обчислюється за формулою

. (4)

Формулу (4) пояснимо на такому прикладі. Нехай дано чотири елемента , комбінаціями з цих елементів по 3 будуть:

.

(Порядок елементів в комбінаціях ролі не грає). Якщо в кожній з цих комбінацій зробити всі можливі перестановки, то дістанемо всі можливі розміщення з чотирьох елементів по 3:

abc	abd	acd	bcd
acb	adb	adc	bdc
bac	bda	cad	cbd
bca	bad	cda	cdb
cab	dab	dac	dbc
cba	dba	dca	dcb

Число таких розміщень дорівнює .

Таким чином, число всіх розміщень з 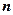елементів по 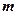дорівнює числу всіх можливих комбінацій елементів по 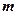, помноженому на число всіх перстановок, які можна зробити із 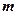елементів, тобто

,

звідки і випливає формула (4).

В данному прикладі

.

Домножимо чисельник і знаменник у формулі (4) на , тоді отримаємо

. (5)

За означенням приймають . Це означення можна отримати із формули (5), якщо прийняти до уваги, що 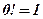(див. зауваження в 1. 2).

Зауваження. При обчисленні числа комбінацій іноді зручно користуватись співвідношенням:

. (6)

Дійсно, якщо за формулою (5) записати , то отримаємо:

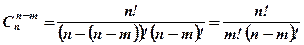. (7)

Останній вираз збігається з правою частиною у формулі (5).

Відмітимо ще, що числа , є коефіцієнтам у біномі Ньютона:

(8)

причому згідно з рівністю (6) коефіцієнти, рівновіддалені від кінців у формулі (8), рівні між собою, тобто,

і т. д.

Приклад 1. Записати за формулою (8) , , , обчисливши біноміальні коефіцієнти за формулами (4) і (6).

Приклад 2. Скількома різними способами можна заповнити картку спортлото, в якій із 49 чисел необхідно вибрати 6 ?

Розв’язання. Дві заповнені картки вважаються різними, якщо серед вибраних 6 чисел вони відрізняються хоча б одним числом, тобто це будуть комбінації, а їх кількість дорівнює:

.

Приклад 3. Скількома способами в даному таймі тренер може виставити на поле 5 баскетболістів, якщо у команді 10 гравців, причому одного із провідних гравців тренер планує задіяти у грі без заміни на весь тайм ?

Розв’язання. Оскільки один з провідних гравців повинен бути постійно у грі весь тайм, то міняти прийдеться тільки 4-х гравців із решти 9, тобто отримаємо

.