 |
|
Неперервні випадкові величини. Функція розподілу, її властивості
Глава VI
Із викладеного матеріалу ми знаємо, що дискретна випадкова величина вважається заданою, якщо відомий її закон розподілу. Закон розподілу дискретної випадкової величини може бути заданий у вигляді таблиці, в якій розміщені всі можливі значення 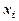 випадкової величини і відповідні їм ймовірності
випадкової величини і відповідні їм ймовірності  .
.
Перейдемо до вивчення неперервної випадкової величини (значення її будемо позначати буквою Х), яка задається на деякому інтервалі (скінченному або нескінченному) так, що її можливі значення заповнюють цей інтервал суцільним чином. Для зручності і більшої загальності будемо припускати, що випадкова величина Х змінюється від 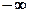 до
до 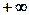 . Якщо ж її значення належать скінченному інтервалу (
. Якщо ж її значення належать скінченному інтервалу (  ), то будемо вважати, що ймовірність попадання випадкової величини за межі інтервалу (
), то будемо вважати, що ймовірність попадання випадкової величини за межі інтервалу (  ) дорівнює нулю.
) дорівнює нулю.
По аналогії з дискретною неперервну випадкову величину задавати за допомогою таблиці всіх можливих значень вже не можна, бо ці значення не злічені, тому закон розподілу неперервної випадкової величиниповинен визначати не ймовірність попадання в точку, а ймовірність попадання на заданий інтервал.
Таким чином для описання неперервної випадкової величини 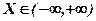 необхідно припустити, що відома ймовірність попадання
необхідно припустити, що відома ймовірність попадання 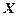 у довільний інтервал, або відома функція розподілу ймовірностей.
у довільний інтервал, або відома функція розподілу ймовірностей.
Означення. Функцією розподілу (інтегральною функцією розподілу) випадкової величини 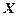 називається ймовірність того, що випадкова величина
називається ймовірність того, що випадкова величина 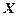 прийме значення менше від фіксованого дійсного числа
прийме значення менше від фіксованого дійсного числа  , тобто
, тобто
 . (1)
. (1)
Геометрична інтерпретація функції розподілу полягає у наступному. Якщо випадкову величину розглядати як випадкову точку на осі  (рис. 1), яка в результаті випробування може зайняти те чи інше положення на цій осі, то функція
(рис. 1), яка в результаті випробування може зайняти те чи інше положення на цій осі, то функція 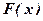 є ймовірність того, що випадкова точка
є ймовірність того, що випадкова точка  у результаті випробування попадає лівіше
у результаті випробування попадає лівіше 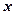 .
.
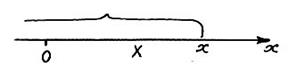
Рис.1
Неперервна випадкова величина має неперервну функцію розподілу, графік якої має форму плавної кривої (рис. 2).

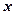
Рис.2
Розглянемо загальні властивості функції розподілу.
Властивість 1. Функція розподілу 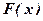 є невід’ємною величиною, яка міститься між нулем і одиницею:
є невід’ємною величиною, яка міститься між нулем і одиницею:
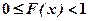 .
.
Дійсно, це випливає з означення 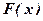 і властивості ймовірності.
і властивості ймовірності.
Властивість 2. Функція розподілу 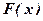 є неспадною функцією, тобто
є неспадною функцією, тобто 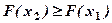 , якщо
, якщо  .
.
Доведення. Нехай  . Подія, яка полягає в тому, що випадкова величина
. Подія, яка полягає в тому, що випадкова величина  приймає значення менше ніж
приймає значення менше ніж  , складається з двох подій:
, складається з двох подій:
1) або  прийме значення менше
прийме значення менше 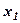 ,
, 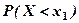 ,
,
2) або 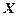 прийме значення з проміжку
прийме значення з проміжку  ,
, 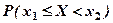 .
.
Тоді за теоремою додавання ймовірностей маємо:
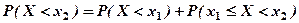


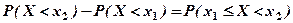 , або
, або
 (2)
(2)
Із формули (2) випливає
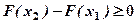 , бо
, бо 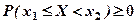 ,
, 

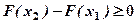 .
.
Наслідок 1.Ймовірність того, що випадкова величина  прийме значення із проміжку
прийме значення із проміжку  , дорівнює приросту функції
, дорівнює приросту функції  на цьому проміжку, тобто
на цьому проміжку, тобто
 (3)
(3)
Приклад 1. Випадкова величина задана інтегральною функцією:

Знайти ймовірність того, що випадкова величина  прийме значення з проміжку [0,2).
прийме значення з проміжку [0,2).
Розв’язання. За формулою (3) маємо:
 , тобто
, тобто
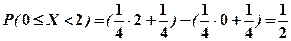 .
.
Наслідок 2. Ймовірність того, що неперервна випадковавеличина  прийме певне значення дорівнює нулю.
прийме певне значення дорівнює нулю.
Доведення. Підставимо у формулу (2)  ,
,  , тоді
, тоді
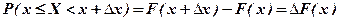 .
.
Нехай 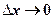 . Оскільки
. Оскільки  - неперервна випадкова величина, то функція
- неперервна випадкова величина, то функція 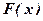 теж неперервна, внаслідок цього маємо, що приріст
теж неперервна, внаслідок цього маємо, що приріст 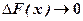 в точці
в точці  , тобто
, тобто 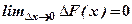 , а значить
, а значить
 (3)
(3)
Підкреслимо, що формула (3) теж тільки для неперервних випадкових величин, на відміну від дискретних.
Враховуючи формулу (3), можна записати
 .
.
Наприклад,

 .
.
Властивість 3. На мінус нескінченності функція розподілу 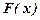 дорівнює нулю, а на плюс нескінченності функція розподілу дорівнює одиниці, тобто
дорівнює нулю, а на плюс нескінченності функція розподілу дорівнює одиниці, тобто
 ;
; 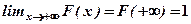 .
.
Зауваження. Сформульоване означення функції розподілу підходить і для дискретної випадкової величини.
Нагадаємо, що функцію розподілу частот ми розглядали у главі II (див. §2.1).
Приклад 2. Скласти функцію розподілу ймовірностей випадкової величини  - числа влучень у ціль трьома стрільцями, які роблять по одному пострілу, якщо ймовірності влучення для кожного з них відповідно дорівнюють 0,8; 0,9; 0,7.
- числа влучень у ціль трьома стрільцями, які роблять по одному пострілу, якщо ймовірності влучення для кожного з них відповідно дорівнюють 0,8; 0,9; 0,7.
Розв’язання. Тут випадкова величина  =0,1,2,3. Позначимо через
=0,1,2,3. Позначимо через  випадкові події влучення у ціль кожним із стрільців, а через
випадкові події влучення у ціль кожним із стрільців, а через 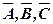 - протилежні події, ймовірності яких відповідно 0,2; 0,1; 0,3. Знайдемо ймовірність появи випадкової величини
- протилежні події, ймовірності яких відповідно 0,2; 0,1; 0,3. Знайдемо ймовірність появи випадкової величини  .
.
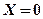 - всі промахи,
- всі промахи,  ;
;
 - одне влучення,
- одне влучення,
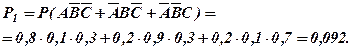
 - два влучення,
- два влучення,

 - три влучення,
- три влучення,
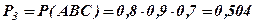 .
.
Запишемо дані в таблицю розподілу:

| 
| 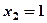
| 
| 
|

| 0,006 | 0,092 | 0,398 | 0,504 |
За даними таблиці знаходимо
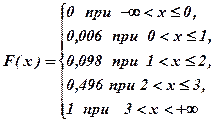
–функцію розподілу для дискретної випадкової величини. Ця функція є кусково-сталою з точками розриву при всіх 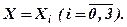 Значення F(x) знаходиться так. У перший інтервал
Значення F(x) знаходиться так. У перший інтервал  не попадає жодне із значень
не попадає жодне із значень  , тому ймовірність 0. Для всіх
, тому ймовірність 0. Для всіх  лівіше знаходиться одне значення
лівіше знаходиться одне значення 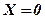 з ймовірністю 0,006, бо
з ймовірністю 0,006, бо

Для всіх значень  , що у третьому інтервалі, лівіше знаходяться два значення
, що у третьому інтервалі, лівіше знаходяться два значення 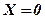 і
і  тому
тому
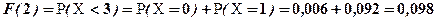
Для всіх значень  лівіше знаходяться два значення
лівіше знаходяться два значення 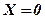 ,
,  і
і 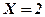 тому
тому

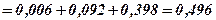 .
.
Для 


Як бачимо функція F(x) аналогічна накопиченим частотам варіаційного ряду. Графік функції F(x) розподілу дискретної випадкової величини даного приклада див. на рис.3.
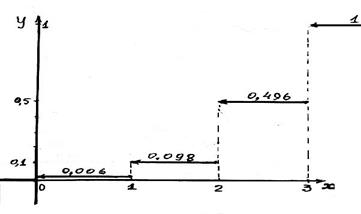
Рис.3