 |
|
Динамика твердого тела и механической системы
Все силы, действующие на механическую систему, разделяют на внешние и внутренние. Ко внешним силам относят активные (заданные) силы и реакции внешних связей. Ко внутренним силам относят реакции внутренних связей – силы взаимодействия между телами (точками), входящими в систему тел (точек). Свойство системы внутренних сил – их главный момент 
и главный вектор 
равны нулю ( 
), ( 
), так как все внутренние силы –силы действия и противодействия между отдельными телами (точками) системы, попарно равны по модулю и противоположны по направлению.
Центр масс системы материальных точек – точка, радиус-вектор 
которой
определяется уравнением: 
, где mi и 
– масса и радиус-вектор i – ой точки механической системы (рис. 3.7а). В проекциях на оси декартовой системы координат, выражения для координат центра масс имеют вид: 
, 
, 
|
| Рис. 3.7. Определение центра масс (а); возможные перемещения рычага (б). |
Центр масс системы материальных точек движется как материальная точка с массой m равной массе всей системы (m = åmi), к которой приложены все внешние силы ( 
), действующие на систему, т.е. уравнение движения центра масс: 
или в проекциях на оси декартовой системы координат дифференциальные уравнения движения центра масс имеют вид: 
, 
, 
.
Импульс системы материальных точек – вектор, равный геометрической сумме (главному вектору) импульсов всех материальных точек этой системы: 
, где 
– скорость движения центра масс. Производная от импульсасистемы материальных точек по времени равна главному вектору внешних сил, действующих на все точки этой системы: 
или в проекциях на оси декартовой системы координат, получим: 
. В случае, когда 
или, выполняется закон сохранения импульса системы материальных точек в целом ( 
) или ( 
) – в проекции на ось x.
В векторной конечной форме теорема об изменении импульсасистемы материальных точек имеет вид: 
или 
или в проекциях на оси декартовой системы координат следует теорема об изменении импульса механической системы в аналитической форме: РKx -Р H x = åSxjвне , РKy - РHy = åSyjвне , РKx - Р H z = å Szjвне.
Момент импульса (кинетический момент) системы материальных точек относительно центра – вектор, равный геометрической сумме моментов импу-льса всех точек системы, взятых относительно этого центра: 
. Момент импульса (кинетический момент) системы материальных точек относительно оси – алгебраическая сумма моментов импульса всех точек системы, взятых относительно этой оси: Lz = å Lzi . Производная от момента импульса системы материальных точек относительно центра по времени равна равна главному моменту всех внешних сил, действующих на все точки этой системы, относительно того же центра: 
или в проекциях на оси декартовой системы координат: dLx/dt = åMx(Fiвне), dLy/dt=åMy(Fiвне) , dLz/dt =åMz(Fiвне) – следует теорема об изменении момента импульса системы материальных точек, записанная в дифференциальной векторной и аналитической формах соответственно. В случае, когда 
или, например, åMx(Fiвне)=0, выполняется закон сохранения момента импульса системы материальных точек относительно центра (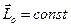 
) или оси координат (Lx =const ).
Кинетическая энергия механической системы равна сумме кинетических энергий всех ее частей (точек, тел): K=åKi. Формулы для вычисления кинети-ческой энергии тела (для основных видов движения тел) приведены в таблице 1. Приращение кинетической энергии механической системы на некотором ее перемещении равно сумме работ всех внешних сил, действующих на все точки (тела) этой системы, на данном перемещении: DK = åAiвне, где KK,KH – кинетическая энергия системы в конечном и начальном положениях.
Абсолютно твердое тело как система из бесконечно большого числа элементарных частиц (материальных точек), бесконечно малое расстояние между которыми всегда неизменно. Поэтому масса твердого – предельное значение суммы масс ее элементарных частиц: m = limåmi.
Моментом инерции тела относительно оси называется величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равна сумме произведений масс всех частиц тела на квадраты их расстояний от этой же оси.
, 
, 
Момент инерции зависит только от формы тела и расположения масс в нем.
Моменты инерции о некоторых однородных тел простейшей формы ( начало координат располагается в центре масс).
1. Прямолинейный тонкий стержень длиной L, расположенный вдоль оси OZ: 
, 
.
2. Прямоугольный параллелепипед со сторонами a, b и с, параллельными соответственно осям OX, OY и OZ:, 
, 
3. Полый прямой круглый цилиндр высотой H и радиусами внешней и внутренней поверхностей, равными R1 и R2; OZ – ось цилиндра: 
, 
.
4. Сплошной прямой круглый цилиндр высотой H и радиусом основания, равным R ; OZ – ось цилиндра: 
, 
.
5. Тонкостенный прямой круглый полый цилиндр высотой H и радиусом основания, равным R ; OZ – ось цилиндра: 
, 
.
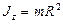6. Полый шар с радиусами внешней и внутренней поверхностей, равными R1 и R2: 
;
7. Сплошной шар: 
;
8. Тонкостенная сфера: 
Радиус инерции тела – расстояние rz от оси вращения z до точки, в которую должна быть сосредоточенна вся масса m тела, чтобы момент инерции этой точки относительно этой оси равнялся моменту инерции тела относительно этой оси: Jz =mrz2 = limåmiri . Момент инерции тела Joz относительно какой-либо оси oz равен сумме момента инерции Jcj тела относительно оси cj, проходящей через центр масс тела, и параллельной оси oz, и произведения массы m тела на квадрат кратчайшего расстояния a между осями: Joz =Jcj +ma2 – теорема о моментах инерции тела относительно параллельных осей (теорема Штейнера).
Решение ряда задач динамики системы, состоящей из твердых тел, предполагает приведение системы сил инерции, действующих на все частицы каждого тела, как правило, к центру масс каждого тела (или другому центру приведения, если это целесообразно). В результате приведения сил инерции к центру, к центру масс, система бесконечно большого числа элементарных сил такому инерции, действующих на все частицы тела, заменяется, в общем случае, одной силой, равной главному вектору сил инерции ( 
) и приложенной в центре приведения (например в центре масс), и одной парой сил, с векторным моментом, равным главному моменту сил инерции, взятому относительно выбранного центра приведения 
.
Таблица 1
Формулы для кинетической энергии тела и работы внешних сил, действующих на тело, и дифференциальные уравнения основных видов движения
| Параметры | Поступательное движение | Вращение вокруг оси | Плоское движение | Сферическое движение | Сложное движение в общем случае |
| Кинетическая энергия | 
| 
| 
| 
| 
|
| Работа внешних сил | 
| 
| 
| 
| 
|
| Дифференциальные уравнения движения |  
| 
| 
| 
| 
|