 |
|
Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.
Диференціальним рівнянням називають рівняння, яке зв’язує незалежну змінну  , шукану функцію
, шукану функцію  та її похідні (або диференціали):
та її похідні (або диференціали):
 , або
, або
 .
.
Порядок диференціального рівняння визначається найвищим порядком похідної (диференціала) цього рівняння.
Розв’язком диференціального рівняння називається функція 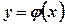 , яка при підстановці у це рівняння перетворює його на тотожність.
, яка при підстановці у це рівняння перетворює його на тотожність.
Диференціальне рівняння першого порядку має вигляд
 , (5.1)
, (5.1)
де 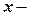 незалежна змінна,
незалежна змінна,  шукана функція,
шукана функція,  похідна шуканої функції.
похідна шуканої функції.
Якщо рівняння можна розв’язати відносно похідної, то його записують у вигляді
 .
.
Розв’язком диференціального рівняння (5.1) на деякому інтервалі  називається диференційована на цьому інтервалі функція
називається диференційована на цьому інтервалі функція  , яка при підстановці в рівняння (5.1) перетворює його на тотожність на
, яка при підстановці в рівняння (5.1) перетворює його на тотожність на  .
.
Функція 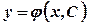 , де
, де 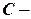 довільна стала, називається загальним розв’язком рівняння (5.1) в області
довільна стала, називається загальним розв’язком рівняння (5.1) в області  , якщо вона задовольняє дві умови:
, якщо вона задовольняє дві умови:
1) функція  є розв’язком рівняння при будь-якому значенні сталої
є розв’язком рівняння при будь-якому значенні сталої  з деякої множини;
з деякої множини;
2) для довільної точки  можна знайти таке значення
можна знайти таке значення  , що функція
, що функція 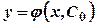 задовольняє початкову умову:
задовольняє початкову умову:
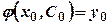 .
.
Частинним розв’язком рівняння (5.1) називається функція 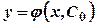 , яка утворюється із загального розв’язку
, яка утворюється із загального розв’язку 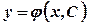 при певному значенні
при певному значенні  .
.
Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді, тобто 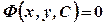 , то такий розв’язок називають загальним інтегралом диференціального рівняння (5.1).
, то такий розв’язок називають загальним інтегралом диференціального рівняння (5.1).
Види диференціальних рівнянь першого порядку:
1. Диференціальні рівняння з відокремлюваними змінними.
2. Однорідні диференціальні рівняння.
3. Лінійні диференціальні рівняння.
4. Диференціальні рівняння Бернуллі.
Диференціальні рівняння з відокремлюваними змінними мають вигляд:
 ,
,
(5.2)
де  і
і  задані і неперервні на деякому інтервалі функції. Вважаючи, що
задані і неперервні на деякому інтервалі функції. Вважаючи, що  , дістанемо
, дістанемо
 або
або  ,
,  . (5.3)
. (5.3)
Рівняння (5.3) називається рівнянням з відокремленими змінними.
Інтегруючи обидві частини останнього рівняння отримаємо загальний інтеграл диференціального рівняння з відокремлюваними змінними:
 .
.
Диференціальне рівняння (5.2) є окремим випадком рівняння виду:
 (5.4)
(5.4)
Для відокремлення змінних у цьому рівнянні досить обидві його частини поділити на добуток  ,
,  .
.
Функція 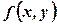 називається однорідною функцією
називається однорідною функцією  го виміру відносно змінних
го виміру відносно змінних  та
та  , якщо для довільного
, якщо для довільного  виконується тотожність:
виконується тотожність:
 .
.
Диференціальне рівняння
 (5.5)
(5.5)
називається однорідним, якщо функція 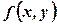 є однорідною функцією нульового виміру, тобто,
є однорідною функцією нульового виміру, тобто,  .
.
Підстановкою  , де
, де  невідома функція, рівняння (5.5) зводиться до рівняння з відокремленими змінними:
невідома функція, рівняння (5.5) зводиться до рівняння з відокремленими змінними:
 .
.
Лінійним диференціальним рівнянням першого порядку називається рівняння виду
 , (5.6)
, (5.6)
де 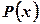 та
та  задані і неперервні на деякому проміжку функції.
задані і неперервні на деякому проміжку функції.
Розв’язок рівняння (5.6) знаходимо у вигляді
 , (5.7)
, (5.7)
де  та
та  невідомі функції, причому одна з них функція довільна (але не дорівнює тотожно нулю). Після підстановки (5.7) в рівняння (5.6) рівняння (5.6) перетворюється на систему 2-х рівнянь з відокремлюваними змінними.
невідомі функції, причому одна з них функція довільна (але не дорівнює тотожно нулю). Після підстановки (5.7) в рівняння (5.6) рівняння (5.6) перетворюється на систему 2-х рівнянь з відокремлюваними змінними.
Рівняння Бернуллі має вигляд
 , (5.8)
, (5.8)
де  .
.
При  рівняння (5.8) буде лінійним, при
рівняння (5.8) буде лінійним, при  рівнянням з відокремлюваними змінними. Метод розв’язання рівняння Бернуллі такий саме як і для лінійного рівняння, тобто розв’язок його знаходимо у вигляді
рівнянням з відокремлюваними змінними. Метод розв’язання рівняння Бернуллі такий саме як і для лінійного рівняння, тобто розв’язок його знаходимо у вигляді  .
.