Главная | Обратная связь

Основні закони комбінаторики

Елементи комбінаторики. Множини

Поряд з числовою множиною можна ввести поняття множини будь-якої природи. Множина вважається заданою, якщо про кожний елемент можна однозначно сказати, чи належить він їй, чи ні.

Множини позначаються великими латинськими літерами, а їх елементи – малими ( ).

Дві множини називаються рівними, якщо вони містять одні і ті ж елементи ( ).

Множина, яка не містить елементів називається пустою, і позначається .

Існують скінченні множини, нескінчені. Скінчену множину можна задати спискомйого елементів.

Два списки елементів однієї і тієї ж множини можуть відрізнятися тільки порядком елементів – число елементів скінченної множини; множина із n елементів називається n-елементною множиною.

Множина впорядкована, якщо її елементи перенумеровані. Нескінчена множина не задається списком, а задається характеристичною властивістю, якою володіють всі елементи множини і не володіють елементи, які не належать цій множині.

Множина 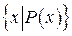– множина елементів x з властивістю .

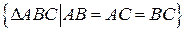( ; – множина рівносторонніх трикутників).

Якщо кожен елемент множини є в той же час елементом множини , то – частина, або підмножина множини , (множина квадратів є підмножиною ромбів).

Перетином множини і називають множину , яка містить елементи як , так і одночасно.

Об’єднанняммножин Х і У називають множину , в яку входять , або .

Різницеюмножин і називають множину , яка містить елементи , але .

Якщо , то є доповненням множини в множині і позначають .

Геометрично операції зображаються діаграмами Ейлера-Венна.

 

 

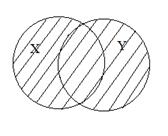
№ 382. Зобразіть за допомогою діаграм Ейлера-Венна:

1.
2.
3.
4.
5.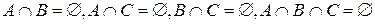
6.

 

Алгебра множин

Для будь-яких множин і виконуються:

І. 1)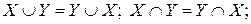

2)

3)

Нехай – універсальна множина, – доповнення до множини , тоді:

4)

5)

6)

Доведемо 6)

Знак читається «тоді і тільки тоді, коли».

Приведений ланцюжок доводить рівність . Мають місце:

Якщо , то

Так як

Приклади

№ 385. Нехай - підмножини універсальної множини . Доведіть, що

1)

2)

Візьмемо доповнення від лівої та правої частини і використаємо приклад 1)

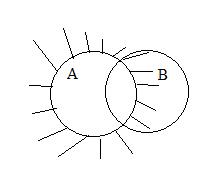
3)

Розпишемо праву частину

(так як ).

Нехай – деяка множина і , – система підмножин із з наступними властивостями:

а) об’єднання всіх множин співпадає з ,

б) якщо , то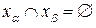

Тоді говорять, що множина розбита на частини , . Нехай в множині задані будь-які підмножини . Кожен елемент із належить одній із цих підмножин і не належать іншим. Цим визначається розбиття множини на частини, які мають вигляд , де для будь-якого множина співпадає або з , або з .

Нехай дано множини

Кортежем довжини , складеним із елементів цих множин, називається скінчена послідовність , де для всіх , маємо: . Елемент називають -тою координатою (або -тою компонентою) кортежа .

Два кортежа і рівні, якщо і для всіх .

Із множин 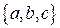і можна скласти 6 кортежей довжини 2: .

Координатами кортежа можуть бути множини, кортежі й т.і. При цьому, наприклад, кортежі і рівні, так як , проте кортежі і різні, так як ( – кортеж; – множина елементів).

Кортеж, який не містить елементів, називається пустим.

Різниця між кортежем та множиною:

а) в множині порядок елементів не грає ролі, а кортежі, які відрізняються порядком елементів, різні навіть у випадку, коли вони мають однаковий склад;

б) в множині всі елементи різні, а в кортежі координати можуть повторюватись.

Нехай – деякі множини. Їх декартовим добутком називають множину кортежем виду , де .

Позначення декартового добутку

Приклад.

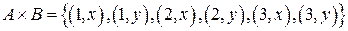
Декартовий добуток складається із пар дійсних чисел (декартові координати).

Декартовий добуток ( множників) називають -мірним арифметичним простором і позначають .

Відповідність, яка спів ставляє кожному елементу один і тільки один елемент , називається відображенням множини в множину .

Приклад. Поставивши у відповідність кожному трикутнику його площу, одержимо відображення множини трикутників в множину .

Елемент множини , який відповідає при відображені елементу , позначають і називають образом елемента .

Якщо , то елемент називають прообразом елемента при відображенні .

Сукупність всіх прообразів елемента при відображенні називають повним прообразом цього елемента і позначають :

Кожній підмножині множини відповідає його образ при відображенні . Цей образ складається із всіх елементів множини , які є образами якого-небудь елемента із :

Кожній підмножині із відповідає його повний прообраз 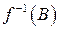при відображенні . Він складається із всіх елементів, образи яких належать :

Множину називають областю визначення відображення , а множину – множиною значень цього відображення.

Якщо при відображенні різні елементи множини переходять в різні елементи множини , то відображення називають зворотним.

Якщо при відображенні кожний елемент множини є образом хоч би одного елемента із (тобто, якщо всі повні прообрази , не пусті), то називають відображенням на , а не в .

Зворотне відображення множини на множину називають взаємно однозначним відображенням на .

Приклад. Роздягальня для пальто. Відображенням, при якому кожному пальто співставляється крючок, є зворотним, якщо на кожному крючку висить не більше одного пальто (деякі крючки можуть бути пусті). Воно є відображенням (множини пальто) на множину (крючки), якщо на кожному крючку висить хоч би одне пальто (на деяких крючк5ах може висіти декілька пальто). Воно є взаємно однозначним відображенням на , якщо на кожному крючку висить рівно одне пальто.

Якщо відображення зворотне, то (кожному відповідає єдиний ). Тоді є оберненим відображенням (множини на ).

Якщо – взаємнооднозначне, то і – взаємнооднозначно.

Якщо – взаємно однозначне на ( – скінченні), то кількість елементів та рівні.

Якщо – зворотне відображення в ( – скінченні), то можна сказати, що в не менше елементів, ніж в . Це твердження формулюється у вигляді принципа Діріхле:

Якщо предметів більше, ніж ящиків, то при будь-якому розподілі елементів по ящиках, хоча б в одному із них буде більше одного предмета.

На мові відображення: якщо в (предмети) більше елементів, ніж в (ящики), то не існує зворотного відображення в .

Якщо – відображення на ( – скінченні), то в – не менше елементів ніж в . Дійсно, виберемо в кожному із повних прообразів елементів по одному елементу. Вибрані елементи утворюють частину множини , яка містить стільки ж елементів, що і . Це й означає, що в не менше елементів, ніж в .

Приклади

№ 405. Побудуйте оберненні відображення для наступних відображень:

1) . Значенням відповідає значення , проте не належить

. Так як , то або

2) . Значенням відповідає значення , проте не належить .

.

По умові

( тільки додатні)

№ 406. Чи існують відображення, обернені до слідуючих:

1) ,

2)

При , проте може приймати значення тільки

Основні закони комбінаторики

При розв’язуванні багатьох практичних задач необхідно вибирати із деякої сукупності об’єктів елементи з деякими спільними властивостями, розкладати їх в деякому визначеному порядку і т.і. Такі задачі називаються комбінаторними, так як вони зв’язані з тими, чи іншими комбінаціями елементів. Область математики, в якій вивчається комбінаторні задачі, називається комбінаторикою.

Приклади.

1. Розмістіть 10 точок і 5 відрізків так, щоб на кожному відрізку було по 4 точки.

2. Розмістити числа 1, 2, 3, …, 9 так, щоб вони утворили «магічний квадрат», тобто квадрат, в якому суми по всіх рядках, стовпчиках і обох діагоналях були однакові.

3. Взнайте, скількома способами можна із 7 хлопчиків і 9 дівчат відібрати команду для естафетного бігу 4+4.

Задачі, в яких потрібно лише знайти число способів розв’язування тієї чи іншої комбінаторної проблеми (не знаходять найкращу, найгіршу комбінацію а т.і.), утворюють частину комбінаторики, яка називається перелічувальною комбінаторикою, або теорією перелічувань (перечислень).

Правило суми.

Якщо елемент можна вибрати способами, а елемент – способами, при цьому будь-який вибір відрізняється від будь-якого , то вибір « або » можна зробити способами.

На мові теорії множин:

Якщо перетин скінченних множин A та B пустий, , то число елементів в їх об’єднанні дорівнює сумі чисел елементів A та B:

Узагальнення:

На мові відображень:

Якщо задано відображення скінченної множини X на Y, то число елементів в Х дорівнює сумі чисел елементів в повних прообразах елементів множини У.

Сформулюємо твердження для множин А, В, які мають непустий перетин.

Для будь-яких скінченних множин А і В має місце рівність

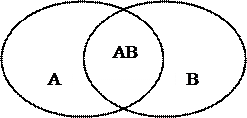
Якщо кількість множин 3, то:

Якщо 4:

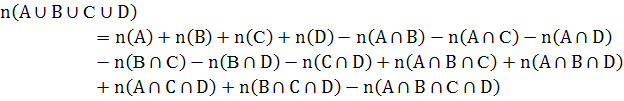
і т. д.

 

Приклад. В класі навчаються 42 учні. Із них 16 приймають участь в секції по легкій атлетиці, 24 – в футбольній секції, 15 – в шаховій секції, 11 – і в секції по легкій атлетиці, і в футбольній, 8 – і в легкій, і в шаховій, 12 – і в футбольній, і в шаховій, а 6 – у всіх трьох секціях. Інші учні захоплюються туризмом. Скільки учнів школи є туристами?

Розв’язання

U – множина всіх учнів, А – члени легкоатлетичної секції, В – футбольної, С – шахової, D – туристичної. По умові задачі

При цьому

;

Отже, туризмом займаються 12 школярів.

Приклад №412. У відділі науково-дослідного інституту працюють декілька співробітників, кожен з них знає хоча б одну іноземну мову. 6 чоловік знає англійську, 6 – німецьку, 7 – французьку, 4 – англійську та німецьку, 3 – німецьку та французьку, 2 – французьку та англійську, 1 – всі три мови. Скільки чоловік працює у відділі? Скільки серед них знає тільки англійську мову? Скільки чоловік знають тільки одну мову?

Розв’язання

А – множина людей, які володіють англійською мовою, Н – німецькою, Ф – французькою.

Всього 11 співробітників, 1 – чистий англічанин, 3 – чистих французів, чистих німців – 0.

Приклад №413. Староста одного класу дав такі відомості про учнів: «В класі навчаються 45 учнів, 25 хлопчиків. 30 учнів навчаються на «4 і 5», в тому числі 16 хлопчиків. Спортом займаються 28 учнів, в тому числі 18 хлопчиків і 17 учнів, які навчаються на «4 і 5» і займаються спортом». Довести, що в цих відомостях є помилка.

Доведення

Із останнього: 15 хл. («4 і 5» );

Із попереднього і останнього:

⁺

18 + 10 =28

Проте з першого слідує: n_дівч.=20, n_дівч.( )=30-16=14,

звідси: n_дівч.( )=20-14=6.

У нас же виходить 8 дівч.( ), що протирічить одне одному.

Приклад №414. Скільки чисел серед перших 100 натуральних чисел не діляться ні на 2, ні на 3, ні на 5?

Розв’язання

Знайдемо, скільки чисел ділиться або на 2, або на 3, або на 5.

n(A2)=50, n(A3)=33, n(A2)=20,

n(A2+A3+A5)=

=n(A2)+n(A3)+n(A5)-n(A2∩A3)-n(A2∩A5)-n(A3∩A5)+n(A2∩A3∩A5)=

=50+33+20-16-10-6+3=74.

n(A2∩A3)=16 (стільки чисел ділиться на 6);

n(A2∩A5)=10 (на10);

n(A3∩A5)=6 (на 15);

n(A2∩A3∩A5)=3 (на 30);

n(A2^’∩A3^’∩A5^’)=100-74=26.

Приклад №415. Скільки чисел серед першої тисячі натуральних чисел не ділиться ні на 2, ні на 3, ні на 5, ні на 7?

Розв’язується аналогічно попередній задачі.

Правило добутку:

Якщо множини А і В скінченні, то число пар в їх декартовому добутку А×В дорівнює добутку чисел елементів цих множин:

n(А×В)=n(A)·n(B)

А також для будь-якої кількості

n(А₁×…×А_m)=n(А₁)·…·n(А_m)

 

Приклад. Скільки номерів із двох букв, за якими йдуть п’ять цифр, можна скласти, використавши 32 букви і 10 цифр?

Розв’язання

Нехай, А – множина із 32 букв, В – множина із 10 цифр. Кожен номер є кортеж декартового добутку

А×А×В×В×В×В×В

n(А×А×В×В×В×В×В)=32·32·10·10·10·10·10=1024·10⁵

На мові відображень:

Нехай задано відображення скінченної множини Х на множину Y, при цьому в кожен елемент Y відображається одне і те ж число елементів Х. Тоді число елементів в Х рівно добутку числа елементів в Y на число елементів, які відображаються в кожен елемент множини Y.

 

Приклад. Скільки впорядкованих пар можна створити із 32 букв, якщо в кожній парі обидві букви різні?

Розв’язання

Поставимо у відповідність кожній парі букв першу букву цієї пари. Одержимо відображення множини Y пар на множину Х букв. Повний прообраз кожної букви (яка стоїть першою в парі) містить 31 букву (всі букви, крім себе). Тому число пар буде 31·32=992.

Можна і по іншому.

Число пар, які дає перша буква – 31, друга – 30, передостання – 1. Всього 1+2+3+…+31=

Врахуємо, що ab і ba різні. Тоді n =31·32=992.

Приклад. Знайдемо число трійок, в яких ніякі дві однакові букви не йдуть підряд. Це трійки (a,b,c), де a≠b і b≠c. При відображенні (a,b,c)→(a,b) кожна пара (a,b) має повний прообраз із 31 трійки. Так число пар рівно 32·31, то число трійок дорівнює 32·31²=30752.

Якщо першу координату кортежу довжини k можна вибрати n₁ способами, при будь-якому виборі першої координати друга вибирається n₂ способами, при будь-якому виборі перших двох координат третя вибирається n₃ способами і т.д. до k^ої координати включно, то загальне число одержаних таким чином кортежей дорівнює n₁ n_2… n_k.

 

При побудові трійок (попередня задача) першу координату можна вибрати 32 способами, другу – 31, третю – теж 31.

n=32·31²=30752.

Приклади

№416. Маємо 5 видів конвертів без марок і 4 види марок. Скількома способами можна вибрати конверти і марку для посилки листа?

Розв’язання

n=5·4=20.

№417. Скількома способами можна вибрати приголосну і голосну із слова «здание», і з слова «паркет»?

Розв’язання

n₁=3·3=9, n₂=4·2=8.

№418. Скількома способами можна вказати на шаховій дошці два квадрати – білий та чорний? Розв’яжіть цю ж задачу, якщо немає обмежень на колір квадратів. Розв’яжіть цю задачу, якщо потрібно вибрати два білих квадрата.

Розв’язання

n₁=32·32=1024,

n₂=63+62+61+…+1=(63·64)/2=2016 (першу клітину – з 63 клітинами, другу клітину – з 62 клітинами і т.д.),

n₃=31+30+29+…+1=(31·32)/2=496.

№419. Скількома способами можна вибрати на шаховій дошці білий та чорний квадрати, які не лежать на одній горизонталі чи одній вертикалі?

Розв’язання

n=32·24=768 (так як кожній із 32 клітин відповідає 24 клітини другого кольору з умови задачі).

№420. Із 3 екземплярів підручника алгебри, 7 екземплярів підручника геометрії, 6 екземплярів підручника фізики потрібно вибрати комплект, який містить всі 3 підручника по одному разу. Скількома способами можна це зробити?

Розв’язання

n=3·7·6=126.

№421. В кошику лежить 12 яблук і 10 апельсин. Ваня вибрав або яблуко, або апельсин, після чого Надя вибирає із залишку фруктів і яблуко, і апельсин. Скільки можливо таких виборів? При якому виборі Вані у Наді більше вибору?

Розв’язання

n_В=22 (бо ж n_В=2, якщо вважати вибір яблука або апельсина як подію незалежно від конкретного фрукту).

n_Н=11·10 або 12·9= 110 або 108.

Більше (n_Н=110), якщо Ваня вибере яблуко.